Dynamisches Chaos
Werbung

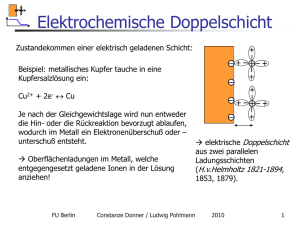
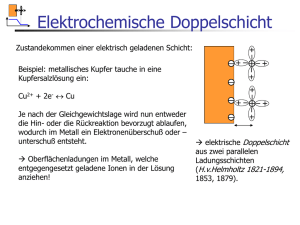
EC-Selbstorganisation 4. Nichtlineare Systeme: Dynamisches Chaos Bisher wurden regelmäßige Oszillationen (d.h. konstante Periodendauer und konstante Amplituden der Schwingungen) als Beispiel zeitlicher elektrochemischer Strukturbildungen betrachtet. Untersucht man aber experimentell oszillierende elektrochemische Systeme, so findet man in den meisten Fällen auch kompliziertere Bewegungen: mehrfach periodische Bewegungen bis hin zu einem scheinbar chaotischen Verhalten! Exkurs zur Chaostheorie ist angebracht! FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 1 EC-Selbstorganisation Der klassische mechanische Determinismus: "Eine Intelligenz, welche für einen gegebenen Augenblick alle in der Natur wirkenden Kräfte sowie die gegenseitige Lage der sie zusammensetzenden Elemente kennte und überdies umfassend genug wäre, diese gegebenen Größen der Analysis zu unterwerfen, würde in derselben Formel die Bewegung der größten Weltkörper wie des leichtesten Atoms umschließen; nichts würde ihr ungewiß sein und Zukunft und Vergangenheit würden ihr offen vor Augen liegen." Pierre Simon de Laplace, Philosophischer Versuch über die Wahrscheinlichkeit, Hrsg. v. R.v. Mises, Leipzig 1932 (Originalausgabe: Paris 1814) FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 2 EC-Selbstorganisation Aber: das gilt nur für lineare Entwicklungsgesetze! Historisches Beispiel: Edward N. Lorenz, Meterologe und Mathematiker (23.Mai 1917 in West Hartford, CT; 16.April 2008 in Cambridge, MA) Lorenz simulierte 1960 ein einfaches Wettermodell auf dem Computer: nur drei Differentialgleichungen, welche Luftströmung und Wärmeleitung beschreiben sollten – aber eben nichtlineare Gleichungen! Ergebnis: zwei Vorhersageläufe mit (scheinbar) gleichen Anfangswerten ergaben nach einiger Zeit völlig verschiedene Wetterprognosen! Empfindlichkeit von den Anfangsbedingungen, „Schmetterlingseffekt“ FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 3 EC-Selbstorganisation Der Lorenz-Attraktor (1963) http://highfellow.git hub.io/lorenzattractor/attractor.ht ml FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 4 EC-Selbstorganisation Der Lorenz-Attraktor (1963): zeitliche Entwicklung: Es gibt immer einen endlichen Vorhersagehorizont! FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 5 EC-Selbstorganisation Der Rössler-Attraktor (1976): Otto E. Rössler, deutscher Biochemiker, geb 1940 in Berlin Inspiriert durch Bonbonknetmaschine (taffy puller) auf Coney Island (O. E. Rössler: An Equation for Continuous Chaos. Physics Letters Vol. 57A no 5, pp 397-398, 1976.) FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 6 EC-Selbstorganisation Der Rössler-Attraktor FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 7 EC-Selbstorganisation A' Topologie des Roessler-Attraktors: A B' Kontraktion B A'' Expansion Bäcker-Transformation Komplette Durchmischung nach nur wenigen Schritten! FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 8 EC-Selbstorganisation Dynamisches Chaos: Auch als „deterministisches Chaos“ bezeichnet: Es ist eine hochstrukturierte Bewegung im Gegensatz zum zufälligen Chaos der Brownschen Bewegung! Dynamisches Chaos ist ein komplexes System mit einem hohen Informationsgehalt Die „seltsamen Attraktoren“ werden u.a. durch eine fraktale Dimesion charakterisiert FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 9 EC-Selbstorganisation Beispiel einer chaotischen Differenzengleichung („Logistische Gleichung“): X(n+1) = A X(n) (1 - X(n)) chaotisch, wenn A = 4 Dreiecke: Rechnung mit 6 Stellen Genauigkeit Quadrate: Rechnung mit 10 Stellen Genauigkeit ein anfänglicher Fehler von nur 0.00005% führt nach nur 23 Wiederholungen zu einem maximalen Fehler von ca. 100%! FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 10 EC-Selbstorganisation H 2 - mass signal/pA Modellbeispiel: Oszillationen bei der kathodischen Reduktion von H2O2 an CuInSe2 (Diss. Günter Neher 1994, Hahn-Meitner-Institut) Regelmäßige galvanostatische Oszillationen: Potential und H2-Entwicklung 20 FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 11 EC-Selbstorganisation Mechanismus: Volmer-HeyrowskiMechanismus: H+ + M + e- -> M-H M-H + H+ + e- -> M + H2 O-Reduktion M + O2 ---> M-O2 M-O2 + e- ---> M-O2M-O2- + M + H2O ---> M-HO2- + M-OH M-OH + e- ---> M + OH- Autokatalyse der H-O-Knallgasreaktion! M-OH + M-H ---> 2M + H2O bei vollständiger H-Belegung: autokatalytische Vermehrung der freien Plätze im mehr positiven Bereich beim Rück-Scan! Pohlmann, L., Neher, G., Tributsch, H., A Model for Oscillating Hydrogen Liberation at CuInSe2 in the Presence of H2O2, Journal of Physical Chemistry 98 (1994) 11007-11010. FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 12 EC-Selbstorganisation j/mAcm-2 Mechanismus: Beweis liegt im ungewöhnlichen Voltammogramm: Experiment potentiostatic galvanostatic U/V/NHE FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 13 EC-Selbstorganisation Mechanismus: Beweis liegt im ungewöhnlichen Voltammogramm: Freie Oberfläche vs. Potential 0.25 V/dt 0.025V/dt 0.0025 V/dt Simulation Es existiert nur ein schmales Potentialfenster, in welchem die Oberfläche frei ist! FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 14 EC-Selbstorganisation Mechanismus: Vergleich der Simulationen mit dem Experiment: (a) Experiment (b) Simulation CddV/dt = (U0 - V)/(RsA) - nFkf(V,x,y)cs dcs/dt = -kf(V,x,y)cs - D(c0 - cs) mit k(V,x,y) = kred(V) (1-x-y), c = [H2O2]surf, c0 = [H2O2]bulk FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 15 EC-Selbstorganisation Übergang zu chaotischer Dynamik im galvanostatischen Regime: i = -1.0 mA i 1s ii iii 1s 5s (c) iv 5s 100 Neher, G., Pohlmann, L., Tributsch, H., Mixed-Mode-Oscillations, Self-Similarity and Time-Transient Chaotic Behavior in the (Photo-)Electrochemical System p-CuInSe2/ H2O2, Journal of Physical Chemistry 99 (1995) 17763-17771. FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 16 EC-Selbstorganisation Übergang zu chaotischer Dynamik im galvanostatischen Regime: FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 17 EC-Selbstorganisation Selbstorganisation in der Elektrochemie: Moderne Forschungen FU Berlin Constanze Donner / Ludwig Pohlmann 2014/2015 18