9. Schwingungen und Resonanz
Werbung

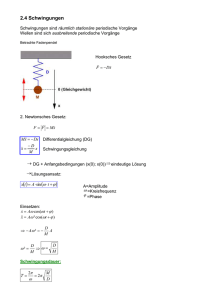
Mechanische Schwingungen und Resonanz Péter Maróti Professor für Biophysik, Universität von Szeged, Ungarn. Lehrbücher: Biophysik für Mediziner (Herausgeber S. Damjanovich, J. Fidy und J. Szöllősi) Medicina, Budapest, 2008. Adam G., Läuger P., Stark G. Physikalische Chemie und Biophysik, Springer-Verlag, Berlin 1988. Fercher A.F. Medizinische Physik, Springer, Wien, New York 1992. Haas U. Physik für Pharmazeuten und Mediziner; Wissenschaftliche Verlagsgesellschaft mbH. Suttgart 2002. Jerrentrup A. Physik für Mediziner, Original-Prüfungsfragen mit Kommentar, Schwarze Reihe, 19. Auflage, Thieme Verlag Stuttgart 2009. Maróti P., Laczkó G.: Bevezetés a biofizikába, JATEPress, Szeged 1998 (Ungarisch) P. Maróti, L. Berkes, F. Tölgyesi: Biophysics Problems. A Textbook with Answers. Akadémiai Kiadó, Budapest 1998 (Englisch). Die mechanische Schwingungen, und Eigenfrequenzen des Körpers mit möglichen Ersatzmodell (VoigtKörper). Die einzelne Schwingungen und Modelle bilden ein weitverzweigtes Netz. elastisches Element: Voigt-Körper Grundfrage: was für eine gekoppelte Bewegung macht der Körper nach (oder auch während) der Anregung? Medizinische Anwendungen der mechanischen Schwingungen Rhythmische Bewegung des Herzes Durch Schwingungen im angegebenen Frequenzbereich hervorgerufene Beschwerden Kopfschmerzen Sprechschwierigkeiten Kieferschmerzen Brustschmerzen Atembeschwerden Bauchschmerzen Kreuzschmerzen Defäkationsdrang Miktionsdrang J.R. Cameron und J.G. Skofronick, 1978 Medizinische Anwendungen der mechanischen Schwingungen Percussio (Klopfen) und Auscultatio (Horchen) L. Auenbrugger hat das Method von „Percussio” und „Auscultatio” schon in 1761 in die medizinische Untersuchung eingeführt. Bestimmte innere Organe werden durch mechanisches Klopfen in Schwingungen gezwungen und vom Horchen der Intensität und Höhe der Eigenschwingungen des Organs, der erfahrene Artz kann auf möglichen Veränderungen (Krankheiten) folgen. Ignác SAUER führte das Method in Ungarn ein. Medizinische Anwendungen der mechanischen Schwingungen Tremor Tremor (Beben, Zittern): unbewusste und rhythmische Bewegung bestimmter Körpersteile (am meissten obere Gliedmassen). Mehr als 10 verschiedene Sorte vom Tremor sind bekannt. Die häufigste Typen sind - das physiologisches Tremor, - das physiologisches Tremor in erhöhtem Grade, - das essentiale Tremor (ET), und - das Parkinson-Tremor (PT). Die charakteristische Bereiche der Frequenze der verschiedenen Typen von Tremor decken sich über: < 4 Hz Cerebellaris und Holmes-Tremor, 4 – 6 Hz 80% des PT und 50% des ET, 6 - 11 Hz physiologisches Tremor, 50% des ET Wie kann man die periodische und 20% des PT und Bewegung beschreiben und > 11 Hz Orthostaticus Tremor. charakterisieren? Medizinische Anwendungen der mechanischen Schwingungen Interventionsradiologie, Lithotripsie Endoskopie in retrograd Der Stein ist im Korb Cholangiopankreatographie. des mechanischen Ein grosser Stein ist in Lithotriptors. Ductus Choledochus. Der Stein wird durch intraendoskopisches Lithotriptor mechanisch eingestampft. Der Korb ist geschrumpft, seine Ausdehnung wurde wesentlich kleiner. Die zertrümmernden Steine liegen im Fokus des Stoβwellengenerators Piezoelektrischer Lithotriptor Nierensteine und Gallenblasensteine lassen sich in vielen Fällen ohne Oparation durch Stoβwellentherapie entfernen. Piezoelektrische Elemente (Kristall) in Form einer Kugelkappe angeordnet. Beispiel des zeitlichen Verlaufs der Stoβwelle eines Lithotriptors. Der Druck steigt innerhalb kürzester Zeit (etwa 30 ns) auf enorm hohe Werte (etwa 40 MPa). Medizinische Anwendungen der mechanischen Schwingungen Augenoperationen mit Laser, KO Stosswellen mit gesundheitsschädlichen Wirkungen werden entstehen, wenn das geschlossene und weiche (flüssige) Organ einen mechanischen Schlag (oder fortwährende Belastung) duch - Bestrahlung des Laserlichtes (das Ort der Absorption wird plötzlich aufwärmen und ausdehnen) oder - (Sport) Unfall (z.B. bei Box) oder - Schäden in der Arbeit (z.B. sitzen im Traktor) erleidet. KO Pardon Medizinische Anwendungen der mechanischen Schwingungen Knochen-, Knorpel- und Gelenk Verletzungen Chronische Überbelastung der Achillessehne. Verletzung der Bänder Knochenbruch durch Strapaze. Definition. Vorgänge oder Bewegungen werden PERIODISCH genannt, wenn sie sich in gleichen Zeitabschnitten wiederholen. g (t ) g (t T ) Here g(t) bezeichnet die zum Zeitpunkt t vorliegenden Wert der physikalischen Gröβe (oder mathematische Funktion). Den kleinsten Wert der zeitlichen Wiederholung (Repetition) nennt man Schwingungs- oder Periodendauer T. Im Zeitraum T erfolgt eine volle Schwingung, d.h. ein Hin- und Hergang, sodass nach der Zeit T alle die Schwingung characterisierenden Gröβen wieder denselben Wert annehmen. Den umgekehrten Wert der Periodendauer nennt man Schwingungs-Frequenz f = 1/T. Die Dimension der Frequenz ist 1/Zeit, und ihre Einheit ist 1/s = 1 Hz. Klassifikation. Nach der konkreten mathematischen Gestalt der g(t) Funktion können wir verschiede Schwingungen einführen. Harmonische Schwingung (Sinusfunktion) g (t ) A sin( t ) Anharmonische Schwingungen: die physikalische Gröβe macht - endliche viele (siehe die geschlossene Lissajous-Kurven) oder - unendlich viele (siehe die Fourier-Theorie) harmonische Schwingungen glechzeitig. Harmonische Schwingung Kinematische Beschreibung. Die Elongation: Abstand von der Mittellage nach Ablauf der Zeit t: x A sin( t ) Die momentane Geschwindigkeit: dx v A cos(t ) dt ist die grösste wenn der Körper durch die Mittellage geht (t = 0, T/2, T, ...) und verschwindet bei den Wendepunkten (t = T/4, 3T/4, ...). Die Beschleunigung: dv a A 2 sin( t ) 2 x dt ist proportional mit der Elongation (x) und (wegen dem Minuszeichen) zeigt immer nach dem Gleichgewichtspunkt. Harmonische Schwingung Dynamische Beschreibung. Die bekannte Funktion zwischen der Beschleunigung und der Zeit wird in das Grundgesetz der Dynamik (zweites Gesetz von Newton) eingesetzt: 2 F m a m x k x Bei harmonischer Schwingung ist in jedem Augenblick die zur Mittellage hin gerichtete Kraft proportional dem Abstand von der Mittellage. 2 2 k m m Die Richtgröβe (Direktionskraft): T 2 m Die Schwingungsdauer der harmonischen Bewegung beträgt: T 2 k Das mathematische Pendel: T 2 l: Länge des Pendels g: Schwerebeschleunigung l g Das physische Pendel: T 2 ΘA mgs ΘA: Massenträgheitsmoment bezogen auf die durch den Aufhängepunkt A gehende Achse m: Masse des pendelnden Körpers s: Abstand Aufhängepunkt - Schwerpunkt Die Energie des Massenpunktes unter harmonischer Bewegung Weil das Kraftfeld konservativ ist, die totale mechanische Energie ändert sich nicht, d.h. sie bleibt konstant: Egesamt 1 1 1 m v 2 k x 2 m 2 A2 Konst 2 2 2 Die Schwingung ist ein periodischer Wechsel zwischen verschiedenen (potentiellen und kinetischen) Energieformen. Überlagerung und Zerlegung von harmonischen Schwingungen 1. Eindimensionale Überlagerung; die Schwingungen zeigen in die selbe Richtung; parallel zueinander verlaufende Schwingungen. a) Schwingungen gleicher Frequenz x1 A1 sin t x 2 A2 sin( t 0 ) Die überlagerte Schwingung ergibt sich nach der Anwendung des Additions-theorems der trigonometrischen Funktion zu: x x1 x2 A sin( t ) Die resultierende Schwingung ist wieder HARMONISCH mit gleicher Frequenz wie die beiden primären Schwingungen, aber davon verschiedener Amplitude A und Phase α A A12 A22 2 A1 A2 cos 0 A2 sin 0 tg A1 A2 cos 0 Spezielfälle: - Wenn die Phasen identisch sind („Zusammenschwingung”, α0 = 0), die Amplituden addieren sich: A = A1 + A2, und die resultierende Phase ist die selbe wie die Phase der Komponente: α = 0. Die Schwingungen verstärken sich einander. - Bei Schwingungen mit entgegengesetzter Phase (α0 = π), die Amplituden subtraktieren sich: A = A1 A2 und die resultierende Phase ist die Phase der Schwingung mit gröβerer Amplitude. Wenn A1 = A2 ist, dann A = 0, d.h. die Schwingungen löschen sich aus. Überlagerung und Zerlegung von harmonischen Schwingungen b) Schwingungen verschiedener Frequenzen: x1 A 1 sin 1t x2 A 2 sin(2t 0 ) Unglücklicherweise, die resultierende Schwingung kann man nicht zur gewöhnliche Form bringen wie oben x x1 x2 A sin(t ) Die Superposition von Schwingungen verschiedener Frequenzen ergibt nur dann eine periodische (nicht aber harmonische) Schwingung, wenn die Frequenzen der einzelnen Schwingungen in einem ganzzahligen Verhältnis stehen: das Verhältnis (ω1/ω2) ist eine rationale Zahl. In diesem Fall ω1 = n1·ω und ω2 = n2·ω (n1 und n2 sind ganze und relative Primzahle), und die Funktion x A1 sin( n1t ) A2 sin( n2t 0 ) ist periodisch mit Periodendauer T = 2π/ω. Überlagerung von harmonischen Schwingungen: Schwebung Ein spezieller Fall der Superposition liegt vor, wenn sich zwei harmonische Schwingungen - gleicher Schwingungsrichtung, - gleicher Phase und - gleicher Amplitude überlagern, deren - Frequenzen sich nur geringfügig voneinander unterscheiden. x1 A sin 1t x2 A sin 2 t Die resultierende Schwingung Der Faktor ändert sich mit der Zeit langsam x x1 x2 2 A cos Die Schwebungsdauer 2 1 TSchwebung 1 2 f1 f 2 1 2 2 schnell t sin 1 2 2 t Die Schwebungsfrequenz fSchwebung f1 f 2 Schwebung Man beobachtet ein periodisches An- und Abschwellen der Amplitude der Schwingung, die sog. Schwebung. Schwebungen spielen groβe Rolle in der Akustik und bei genauen Frequenzmessungen. Die Schwebung stellt einen Speziellfall der amplitudenmodulierten Schwingungen dar. Überlagerung von harmonischen Schwingungen, die Lissajous-Figuren 2. Zweidimensionale Überlagerung Die Schwingungsrichtungen stehen senkrecht aufeinander und die beiden Schwingungen haben a) verschiedene Frequenzen: x A sin a t y B sin( b t ) Die resultierende Schwingung hat eine umso kompliziertere Form, je stärker das Verhältnis der beiden Frequenzen von 1 abweicht. b) die gleiche Frequenz: elliptische Schwingungen x A sin t y B sin( t ) sin( t ) sin t cos cos t sin Bei verschiedenen Werten des Phasenwinkels ergeben sich elliptische Schwingungen mit unterschiedlichen Achsenverhältnissen (siehe die nächste Seite), die jeweils nur für α = 0 oder α = π in geradlinige Schwingungen entarten. Anfangsphase α x y Analytische Gleichung der Kurve y B x A 0o A· sin(ωt) B· sin(ωt) 90o A· sin(ωt) B· cos(ωt) 180o A· sin(ωt) -B· sin(ωt) 270o A· sin(ωt) -B· cos(ωt) Darstellung y x y 2 2 x y 1 A B y B x A x y x y 2 2 x y 1 A B x Beispiel: elliptische Schwingungen x A sin t y B sin( t ) B sin t cos B cos t sin Die Zeit wird eliminiert (mit Anwendung von sin ωt = x/A und cos2 ωt + sin2 ωt = 1): y x x2 cos 1 2 sin B A A x2 y x 2 cos 1 2 sin A B A x 2 y 2 2 xy 2 cos sin 2 2 AB A B Das ist die analytische Gleichung einer Ellipse, welche für A = B in einen Kreis übergeht. Die x und y Koordinaten können Werte aufnehmen, die kleiner als A bzw. B sind. Die Ellipse liegt in einem Rechteck mit Seiten A und B und das Zentrum des Rechtecks ist der Anfangspunkt der beiden Schwingungen. 2 y x B A Zerlegung von anharmonischen Schwingungen, Fourier-Analyse Fourier-Theorem: beliebige periodische Funktion g(t), g (t ) g (t T ) kann in harmonischen Anteile zerlegen. Neben der Grundschwingung (oder Fundamentalschwingung) mit der Frequenz ω treten auch die harmonischen Oberschwingungen auf, mit Frequenzen, die ganzzahlige Vielfache der Grundfrequenz (ωi = i·ω (i = 1,2,...)) sind: Erste Oberschwingung Erste Oberschwingung g(t) = A0/2 + A1cosωt + A2cos2ωt + ...+ B1sinωt + B2sin2ωt +... Grundschwingung Grundschwingung Die Amplituden Ai und Bi (i = 0,1,2,...) (Fourierkoeffizienten) werden durch die folgenden Integralen bestimmt: T 2 Ai g (t ) cos(it ) dt T0 T 2 Bi g (t ) sin( it ) dt T0 (i 0,1,2,3,...) Beispiel: Fourier-Zerlegung der Rechteckschwingung 1 1 1 1 x(t ) (sin t sin 3t sin 5t sin 7t ...) 3 5 7 Jede zweite (gerade) Glieder der FourierReihe entfallen, d.h. die A2, A4,... und B2, B4, ... einzelner Oberschwingungen sind gleich null. Je mehr FourierKoeffizienten berücksichtigt werden, desto präziser kann die periodische Funktion approximiert werden. Gedämpfte Schwingungen Federkraft: Reibungskraft: F1 = -k·x F2 = -η·v Feder Feder Dämpfer Dämpfer Körper Körper Kraft Verschiebung Periodische Bewegung des Voigt-Körpers 0 2m k m Die Reibung (Dämpfung) ist klein. Feder Dämpfung d 2x dx m 2 k x dt dt Die Kreisfrequenz der Schwingung verkleinert sich durch die Reibung: 2 0 2 Die Lösung der Bewegungsgleichung: x A e t sin( t ) Aperiodische Bewegung des Voigt-Körpers; die Dämpfung ist groβ: κ > ω0 Die analytische Lösung mit x(t=0) = 0 und v(t=0) = v0 Anfangsbedingung: x v0 2 02 e t sh 2 02 t wo sh (x) ist die sogennante „Sinus Hyperbolicus” Funktion: sh x exp( x) exp( x) 2 Die Dämpfung ist so groβ, dass der „schwingende” Körper bleibt an einer Seite und kann zum Anfangspunkt nur nach unendlich langer Zeit monotoner Weise zurückkehren (er „kriecht” gegen Null). Die Bewegung ist nicht mehr periodisch, sondern aperiodisch. Beispiel: Bewegung eines Pendulums in zähiger Flüssigkeit (z.B. Honig). Erzwungene Schwingungen Erzwungene Schwingungen treten immer dort auf, wo äuβere periodische Kräfte (F0·sin(ωt)) auf ein schwingungsfähiges (und gedämpftes) System einwirken. Die erzwungene Schwingungen erfolgen mit einer Frequenz, die im Allgemeinheit nicht der Eigenfrequenz (ω0) des schwingenden Systems entspricht, sondern der sie erzeugenden Kraft (ω). Die Bewegungsgleichung: d 2x dx m dt 2 k x dt F0 sin t Die allgemeine Lösung im Fall von κ < ω0 (kleine Dämpfung) x(t ) A cos(t ) ae Periodisches Glied (Schwingung) wo A F0 / m 4 2 2 2 2 2 0 stationäre Amplitude t sin t 2 0 2 Transient und gedämpftes Glied, welches nach beliebiger Zeit sich verschwindet. 2 tg 2 0 2 Phasenverschiebung Resonanz Amplitude, Resonanzkurven Dämpfung k 0 m 2m Phase Bei einem ungedämpften System steigt die Amplitude der Schwingung ins Unendliche an, wenn die Kresfrequenz des Erregers mit der Eigenfrequenz der freien, ungedämpften Oszillation übereinstimmt (Resonanzkatastrophe). Eine Dämpfung des Systems begrenzt die Amplitude auf endliche Werte. Mit steigender Dämpfung sinkt die Resonanzamplitude ab und das Resonanzmaximum verschiebt sich geringfügig zu kleineren Frequenzen. Für verschwindende Dämpfung zeigt die Phasenverschiebung einen sprunghaften Verlauf; mit steigender Dämpfung wird der Übergang stetig und zunehmend breiter. Im Resonanzfall eilt die erregende der erzwungenen Schwingung um π/2, d.h. um eine viertel Periode voraus. Aufgaben 1) Ein Massenpunkt schwingt harmonisch mit einer Kreisfrequenz 6,28 s-1. Wie groβ ist die Zeit, die sie benötigt, um sich von einem zum anderen Umkehrpunkt zu bewegen? 2) Zwei (harmonische) Pendel der Schwingungsfrequenzen 3 Hz und 0,5 Hz werden in die gleiche Richtung ausgelenkt und dann gleichzeitig losgelassen. Nach welcher Zeit befinden sich beide Pendel estmals zusammen wieder in dieser Ausgangslage? 3) Die Masse eines leeren Personenwagens ist 800 kg. Wenn 5 Personen (500 kg) im Wagen Platz nehmen, die Karosserie sinkt 6 cm. Was ist die Schwingungsdauer des Autos im belasteten bzw. unbelasteten Zustand? 4) Ein Holzscheit schwimmt auf der Oberfläche des Wassers. Wir drücken es leicht in das Wasser und lassen wir los. Wie groβ ist die Schwingungsdauer des Holzscheites? 5) Zwei harmonische Schwingungen mit den Frequenzen 1 kHz und 2 kHz werden überlagert. Ist die resultierende Schwingung - harmonisch oder anharmonisch - periodisch und wenn ja, wie groβ ist ihre Periodendauer? 6) Die Periode einer nichtharmonischer Schwingung beträgt T = 0,5 ms. Welches sind die Frequenzen der ersten drei Oberschwingungen? Aufgaben 7) Die gedämpfte Schwingung kann zur Bestimmung der inneren Reibung verschiedener Flüssigkeiten dienen. Der Massenpunkt (Masse m = 1 kg) eines mathematischen Pendels (Länge l = 2 m) wird aus der Ruhelage mit A1 = 10 cm ausgelenkt und dann losgelassan. Die Bewegung des Massenpunktes erfolgt nicht in Luft (Vakuum) aber in einer Flüssigkeit was die Schwingung des Pendels (starker oder weniger, je nach ihrer Viskosität) dämpft. So, bei dem Rückkehr des Massenpunktes zu der Anfangsposition, die Amplitude (die maximale Auslenkung) verringert sich auf A2 = 8 cm. a) Wie groß wird die nächste Auslenkung in diese Richtung (A3)? b) Was ist die Viskosität (η, die Koeffizient der inneren Reibung) der Flüssigkeit? 8) Verbinden Sie zwei Feder mit verschiedenen Federkonstanten seriell und parallel. Wie kann man die zwei Feder mit einem (resultierenden) Feder ersetzen? 9) Die Eisenbahnwagen werden durch regelmäßigen Stoßen von den nicht ganz glatten Gleisverbindungen in (erzwungener) Schwingung kommen. Die Masse eines Wagens ist 2,2 ·104 kg, die Feder des Wagens drücken sich 1,6 μm unter 1 N Kraft und die Eisenbahn ist aus 18 m langen Gleisstücken gebaut. Bei welcher Geschwindigkeit erreicht die Auslenkung des Wagens den grőßten Wert (d.h. schwinkt der Wagen am besten)? Aufgaben 10) Ein Massenpunkt mit Masse m ist am Ende eines Maxwell Körpers gesetzt. (Der Maxwell Körper besteht aus einer Feder (k) und einem Dämpfer (κ) in Series geschaltet.) Schreiben Sie die Bewegungsgleichung des Massenpunktes auf!