Ф (a i ) für λ = 0,4

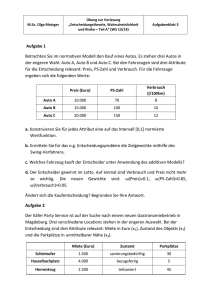
Präskriptive
Entscheidungstheorie
5 Entscheidungen bei
Ungewissheit und Risiko
Gliederung
5 Entscheidungen bei Unsicherheit
5.1 Entscheidungen bei Ungewissheit
5.1.1 Maximin-Regel
5.1.2 Maximax-Regel
5.1.3 Hurwicz-Regel
5.1.4 Savage-Niehans-Regel
5.1.5 Laplace-Kriterium
5.2 Entscheidungen bei Risiko
5.2.1 Bayes-Regel
5.2.2 (μσ)-Prinzip
5.2.3 Bernoulli-Prinzip
Das Grundmodell
Ziele
Z
Umfeld-
u1
u2
a1
e11
e12
a2
e21
zustände
u3
Alternativen


e22
e13
e23
Im Folgenden gehen wir von einem Ziel aus, betrachten
aber mehrere mögliche Umfeldzustände.
Für den Eintritt der Umfeldzustände sind keine
Wahrscheinlichkeiten bekannt → Ungewissheit.
Beispiel
u1
u2
u3
u4
a1
60
30
50
60
a2
10
10
10
140
a3
-30
100
120
130


Für eine Entscheidung bei Ungewissheit sei
obige Ergebnismatrix gegeben.
Wie würden sie entscheiden?
5.1.1 Maximin-Regel (MinimaxRegel)


Man wählt die Alternative, die im ungünstigsten Fall noch das beste
Ergebnis bringt, hier also Alternative 1 mit dem Minimum von 30.
Maximin!
Wenn die Zahlen in der Matrix für einen Schaden stehen, dann
minimiert man den maximalen Schaden. Auch dabei wäre
Alternative 1 am besten, da der maximale Schaden dann nur 60
beträgt. Minimax!
u1
u2
u3
u4
Minimum
a1
60
30
50
60
30
a2
10
10
10
140
10
a3
-30
100
120
130
-30
Kritik an der Maximin-Regel


Der Entscheidungsträger ist extrem risikoscheu bzw. pessimistisch,
da er immer vom schlechtesten möglichen Zustand ausgeht.
Es geht nur ein Ergebnis in die Bewertung ein. Das wird um so
unsinniger, je weiter die Ergebnisse streuen. Im Beispiel unten wäre
Alternative 2 nach der Maximin-Regel vorzuziehen.
u1
u2
u3
u4
Minimum
a1
1.000.000 1.000.000 0,99
1.000.000 0,99
a2
1
1
1
1
1
5.1.2 Maximax-Regel

Man wählt die Alternative, die im günstigsten Fall
das höchste Ergebnis bringt. Hier also
Alternative 2. Maximax!
u1
u2
u3
u4
Maximum
a1
60
30
50
60
60
a2
10
10
10
140
140
a3
-30
100
120
130
130
Kritik an der Maximax-Regel


Der Entscheider ist extrem risikofreudig bzw. optimistisch, da er nur
vom bestmöglichen Zustand ausgeht. Die meisten Menschen sind
eher risikoscheu.
Sich nur an einem Ergebnis zu orientieren, kann besonders dann zu
falschen Entscheidungen führen, wenn die Ergebnisse stark
streuen. Nach der Maximax-Regel wäre im Beispiel unten
Alternative 1 vorzuziehen.
u1
u2
u3
u4
Maximum
a1
1
1
150
1
150
a2
100
120
130
130
130
5.1.3 Hurwicz-Regel
Die Maximin und die Maximax-Regel
werden kombiniert.
 Ein Optimismusparameter λ, der zwischen
0 und 1 liegt, gewichtet das minimale und
das maximale Ergebnis.
 Für jede Alternative ai errechnet sich der
Präferenzwert durch
Ф(ai) = λ x maxj (eij) + (1- λ) x minj (eij)

Beispiel für die Hurwicz-Regel
u1
u2
u3
u4
Max
Min
Ф (ai) für λ = 0,4
a1
60
30
50
60
60
30
0,4 x 60 + 0,6 x 30 = 42
a2
10
10
10
140
140
10
0,4 x 140 + 0,6 x 10 = 62
a3
-30
100
120
130
130
-30
0,4 x 130 + 0,6 x (-30) = 34


Der Parameter λ spiegelt den Optimismus wider. Ist λ =1, dann ist der
Entscheider sehr optimistisch und lässt nur das beste Ergebnis einfließen
(=Maximax). Ist λ = 0, dann ist er pessimistisch und richtet sich nur am
Minimum aus (=Maximin).
Mit Werten für λ zwischen 0 und 1 kann man beide Werte einfließen lassen.
Je näher λ bei 1 liegt, desto optimistischer ist der Entscheider. Hier: λ = 0,4.
Kritik an der Hurwicz-Regel


Es werden immerhin zwei Ergebniswerte berücksichtigt. Da es sich
aber um die Extremwerte handelt, kann auch diese Regel zu
falschen Entscheidungen führen.
Berechnet man den Präferenzwert nach der Hurwicz-Regel, dann
sind Alternative 1 und 2 gleichwertig, obwohl Alternative a2 eindeutig
besser ist.
u1
u2
u3
u4
Max
Min
Ф (ai) für λ = 0,4
a1
1
0
0
0
1
0
0,4 x 1 + 0,6 x 0 = 0,4
a2
0
1
1
1
1
0
0,4 x 1 + 0,6 x 0 = 0,4
5.1.4 Savage-Niehans-Regel
u1
u2
u3
u4
a1
60
30
50
60
a2
10
10
10
a3
-30
100
120


u1
u2
u3
u4
a1
60 -60 = 0
70
70
80
140
a2
60-10 = 50
90
110
0
130
a3
60-(-30) = 90
0
0
10
Zunächst wird eine Matrix des Bedauerns aufgestellt. Dazu
bestimmt man für jeden möglichen Umfeldzustand die Alternative,
die das maximale Ergebnis bringen würde (rot geschrieben).
Daraus ergibt sich die Bedauernsmatrix (rechts), indem von dem
Spaltenmaximum das jeweilige Ergebnis abgezogen wird.
Savage-Niehans-Regel
u1
u2
u3
u4
Maximum
a1
0
70
70
80
80
a2
50
90
110
0
110
a3
90
0
0
10
90


Die Bedauernsmatix wird auch als Opportunitätskostenmatrix oder
Nutzenentgangsmatrix bezeichnet. Sie gibt an, was ich dadurch
„verliere“, dass ich beim Eintritt eines Umfeldzustandes uj nicht die
Alternative gewählt habe, die dann am besten gewesen wäre.
Man wählt die Alternative, bei der das maximale Bedauern minimal
ist, also hier Alternative 1.
Kritik an der Savage-NiehansRegel



Es gehen wieder nicht alle Werte in die
Entscheidung ein, sondern nur Extremwerte.
Der Entscheider ist sehr pessimistisch, weil er
vom schlechtesten möglichen Fall ausgeht.
Die Rangfolge zwischen zwei Alternativen a1
und a2 kann sich dadurch verändern, dass eine
dritte Alternative hinzukommt.
5.1.5 Laplace-Kriterium



Es wird einfach der Durchschnitt der Ergebnisse für alle
Umfeldzustände gebildet.
Es wird unterstellt, dass alle Umfeldzustände gleich wahrscheinlich
sind.
Das entspricht der Berechnung des Erwartungswertes in
Risikosituationen.
u1
u2
u3
u4
Фai
a1
60
30
50
60
(60 + 30 + 50 + 60):4 = 50
a2
10
10
10
140
(10 + 10+ 10 + 140):4 = 42,5
a3
-30
100
120
130
(-30 + 100 + 120 + 130):4 = 80
Kritik am Laplace-Kriterium



Positiv ist, dass alle Werte in die Entscheidung
einfließen.
Passt nur für einen risikoneutralen Entscheider.
Man kann sich fragen, ob tatsächliche alle
Umfeldzustände gleich wahrscheinlich sind.
Wenn nicht, sollte man den Umfeldzuständen
Wahrscheinlichkeiten zuordnen, also zu einer
Entscheidung bei Risiko übergehen.
Rationalität der Entscheidung

Entscheidungsregel
Optimale Alternative
Maximin
a1
Maximax
a2
Hurwicz (mit λ = 0,4)
a2
Savage-Niehans
a1
Laplace
a3
Die Entscheidung fällt je nach Regel
unterschiedlich aus. Sind die Regeln deshalb
Unsinn?
Rationalität der Entscheidung


Die unterschiedlichen Ergebnisse drücken die
unterschiedliche Einstellung des Entscheiders zum
Risiko aus. Für einen Pessimisten ist es subjektiv
rational, vom schlechtesten Ergebnis auszugehen.
Die Entscheidungsregeln genügen aber tatsächlich nicht
allen Rationalitätsanforderungen:
- Bei der Maximin, der Maximax und der Hurwicz-Regel kann eine
Alternative als optimal gelten, die von einer anderen dominiert wird.
- Bei der Savage-Niehans-Regel kann sich die Präferenz zwischen
zwei Alternativen dadurch ändern, dass eine dritte Alternative
dazukommt.
5.2 Entscheidung bei Risiko
Ziele
Z
u1
u2
w1
w2
w3
a1
e11
e12
e13
a2
e21
Umfeldzustände
Alternativen


W
e22
u3
e23
Es werden nun Eintrittswahrscheinlichkeiten für die
Umfeldzustände angegeben.
Diese können objektiv oder subjektiv sein.
Beispiel
U1
W1 = 0,3
U2
W2 = 0,5
U3
W3 = 0,2
a1
90
110
150
a2
95
105
120

Wie würden Sie entscheiden?
5.2.1 Bayes-Regel (μ-Prinzip)



Man gewichtet das beim Umweltzustand j eintretende
Ergebnis eij mit der Eintrittswahrscheinlichkeit wj.
Die so gewonnenen Produkte werden addiert und der
Erwartungswert μ ermittelt. μ = E(ai) = ∑ eij wj
Wähle die Alternative mit dem höchsten Erwartungswert!
U1
W1 = 0,3
U2
W2 = 0,5
U3
W3 = 0,2
μ
a1
90
110
150
0,3 * 90 + 0,5 * 110 + 0,2 * 150 = 112
a2
95
105
120
0,3 * 95 + 0,5 * 105 + 0,2 * 120 = 105
Kritik an der Bayes-Regel



Die Bayes-Regel hat den Vorteil der Einfachheit.
Sie liefert gute Ergebnisse bei Entscheidungen,
die häufig anfallen, da sich nach dem Gesetz
der großen Zahl dann die Ergebnisse dem
Erwartungswert annähern.
Sie passt allerdings nur für risikoneutrale
Entscheider, da die Streuung der Ergebnisse
nicht berücksichtigt wird.
5.2.2 (μσ)-Prinzip


Bei dieser Entscheidungsregel wird zusätzlich zum
Erwartungswert μ die Streuung berücksichtigt.
Die Streuung erfasst man über die Standardabweichung
nach der Formel σ = √ ∑wj (eij – μi)2
U1
W1 = 0,3
U2
W2 = 0,5
U3
W3 = 0,2
μ
σ
a1
90
110
150
112
20,88
a2
95
105
120
105
8,66
(μσ)-Prinzip


Der Entscheider drückt seine Risikopräferenz über den
Einbezug von σ in seine Präferenzfunktion aus.
Bewertet er die Streuung negativ, dann ist er
risikoscheu, bewertet er sie positiv, dann ist er
risikofreudig.
μ
U1
U2
U3
W1=0,3
W2=0,5
W3=0,2
a1
90
110
150
112
a2
95
105
120
105
σ
Ф = μ - 2σ
Ф = μ + 2σ
(risikoscheu)
(risikofreudig)
20,88
70,24
153,76
8,66
87,68
122,32
Kritik am μσ-Prinzip
An dieser Entscheidungsregel wird
kritisiert, dass Alternativen auch bei
gleichem Erwartungswert und gleicher
Streuung sehr unterschiedlich aussehen
können.
 Es kann passieren, dass eine dominante
Alternative den niedrigeren Präferenzwert
bekommt.

5.2.3 Bernoulli-Prinzip



Benannt nach Daniel Bernoulli, der 1738 einen
Aufsatz veröffentlichte, auf dem die
Entscheidungsregel beruht.
Wird auch als Erwartungsnutzentheorie
bezeichnet.
Die Ergebnismatrix wird zunächst in eine
Nutzenmatrix überführt. Jedem Ergebnis eij wird
ein Nutzen n(eij) zugeordnet, der sich nach der
Höhen- und Risikopräferenz des Entscheiders
richtet.
Bernoulli-Prinzip

Aus den Nutzwerten wird durch Gewichtung mit
den Wahrscheinlichkeiten der Erwartungswert
bestimmt. Daher auch Erwartungsnutzentheorie.

Entscheidungsprinzip: Wähle die Alternative mit
dem höchsten Erwartungsnutzen!
Ф(ai) = ∑ nij wj max!
Bedeutung von Risikopräferenzen
a1
U1
W1 = 0,5
200
U2
W2 = 0,5
200
a2
100
300



a1 = a2, der Entscheider ist risikoneutral.
a1 > a2, der Entscheider ist risikoscheu.
a1 < a2, der Entscheider ist risikofreudig.
Risikonutzenfunktion

Die unterschiedliche subjektive Einstellung zum Risiko
bringt der Entscheider bei der Erwartungsnutzentheorie
über die Risikonutzenfunktion (RNF) zum Ausdruck, mit
deren Hilfe er die Ergebnisse in Nutzwerte umrechnet.

Die Ermittlung der RNF ist schwierig und erfolgt über die
sog. Bernoulli-Befragung.

Es gibt verschiedene Methoden der Befragung, die auf
gemeinsamen Grundüberlegungen basieren.
Bernoulli-Befragung



Der Entscheider muss sagen,
wann er indifferent ist zwischen
einem sicheren Betrag (a1) und
den Chancen aus einer Lotterie
(a2), bei der er mit Wahrscheinlichkeit w mehr bekommt als den
sicheren Betrag und mit Wahrscheinlichkeit 1-w weniger.
Die riskante Alternative 2 nennt
man Basis-Referenz-Lotterie.
Der sichere Betrag, der den
gleichen Nutzen hat wie die
Lotterie, wird
Sicherheitsäquivalent genannt.
1
Sicherer Betrag
Maximaler Betrag mit
Wahrscheinlichkeit w
2
Minimaler Betrag mit
Wahrscheinlichkeit 1-w
Bernoulli-Befragung

Im Falle der Indifferenz zwischen a1 und a2 gilt:
Erwartungsnutzen der Basis-Referenz-Lotterie = Nutzen des Sicherheitsäquivalents.
EN (BRL) = w * n (emax) + (1-w) * n (emin) = n (SÄ)

Setze ich den Nutzen für das minimale Ergebnis
mit 0 fest und für das maximale Ergebnis mit 1
dann gilt:
EN (BRL) = w = n (SÄ)
Bernoulli-Befragung
In der Formel EN(BRL) = w = n(SÄ)
stecken 4 Größen: Die Wahrscheinlichkeit
w, die beiden Ergebnisse emin und emax
und das Sicherheitsäquivalent.
 Methoden zur Ermittlung der
Nutzenfunktion unterscheiden sich
danach, welche dieser Größen gegeben
sind und nach welcher gefragt wird.

Bernoulli-Befragung
Die Lotterie ist gegeben und es wird nach
dem Sicherheitsäquivalent gefragt:
Welchen sicheren Betrag würden sie einer
Lotterie gleich stellen, bei der sie mit der
Wahrscheinlichkeit 0,4 1000 € bekommen
und mit der Wahrscheinlichkeit 0,6 nichts?
 Certainty equivalent methods: MittelwertKettungs-Methode, Fraktilmethode.

Bernoulli-Befragung


Man gibt das Sicherheitsäquivalent vor und fragt
nach der Wahrscheinlichkeit, bei welcher die
Lotterie als gleichwertig empfunden wird:
Wie hoch muss die Wahrscheinlichkeit für einen
Betrag von 1000 € sein, damit die Lotterie ihnen
400 € wert ist?
Probability-equivalent-methods: Methode
variabler Wahrscheinlichkeiten, LotterieVergleich-Methode.
Methode variabler
Wahrscheinlichkeiten

Man bestimmt zwei Ergebniswerte, einen maximalen
und einen minimalen und ordnet ihnen Nutzen zu.
emax = 1000
n(1000) = 1
emin = 0
n(0) = 0

Der Entscheider soll wählen zwischen einem sicheren
Ergebnis von 400 (SÄ) und einer Lotterie, in welcher er
mit Wahrscheinlichkeit w 1000 € und mit Wahrscheinlichkeit 1-w 0 € bekommt.
W sei zunächst 0,5.
Methode variabler
Wahrscheinlichkeiten
Der Entscheider wähle im ersten
Durchgang a1, d.h. 400 € sicher sind ihm
lieber als die fifty-fifty-Chance auf 1000 €.
 Die Wahrscheinlichkeit wird variiert. Als
Alternative 2 wird eine Lotterie angeboten,
bei der die Wahrscheinlichkeit 1000 € zu
gewinnen auf 0,6 gestiegen ist.

Methode variabler
Wahrscheinlichkeiten



Der Entscheider wähle nun a2.
Da man die Wahrscheinlichkeit sucht, bei
welcher der Entscheider indifferent wird
zwischen a1 und a2, wählt man im dritten
Durchgang eine Wahrscheinlichkeit zwischen
0,5 und 0,6, bspw. 0,55.
Die Wahrscheinlichkeit wird solange variiert, bis
dem Entscheider die Lotterie genauso viel wert
ist, wie die 400 € Sicherheitsäquivalent.
Methode variabler
Wahrscheinlichkeiten

Der Entscheider werde indifferent bei w = 0,58. Nach der
Gleichung
EN(BRL) = w = n(SÄ)
entspricht w dem Nutzen des Sicherheitsäquivalents.

Damit hat man einen ersten Wert für die Nutzenfunktion
n(400) = 0,58.

Auf diese Weise kann man für mehrere
Sicherheitsäquivalente den Nutzen ermitteln und die
zugehörige Nutzenfunktion zeichnen.
Erkennen der Risikopräferenz



Die Risikopräferenz des Entscheiders ergibt sich aus
einem Vergleich seines Sicherheitsäquivalents mit dem
Erwartungswert der Lotterie.
In der ersten Runde waren dem Entscheider sichere
400 € lieber als eine 50%ige Chance auf 1000 €. Sein
Sicherheitsäquivalent liegt unter dem Erwartungswert
von 500 €. Damit ist er risikoscheu.
Die Differenz zwischen dem Erwartungswert und dem
SÄ (E – SÄ) nennt man Risikoprämie. Der Entscheider
verzichtet quasi auf 100 €, um auf Nummer sicher zu
gehen.
Nutzenfunktion und
Risikopräferenz



Eine lineare Nutzenfunktion
spiegelt einen risikoneutralen
Entscheider wider. SÄ = E
Eine konvexe Nutzenfunktion
spiegelt einen risikofreudigen
Entscheider wider. SÄrf > E
Eine konkave Nutzenfunktion
spiegelt einen risikoscheuen
Entscheider wider. SÄrs < E
n
N rs
N rf
0,5
SÄ rs
e
E
SÄ rf
Erkennen der Risikopräferenz
Risikoscheu
Sicherheitsäquivalent Risikoprämie positiv
kleiner als
Konkave Nutzenfunktion
Erwartungswert
Risikofreude
Sicherheitsäquivalent Risikoprämie negativ
größer als
Konvexe Nutzenfunktion
Erwartungswert
Risikoneutralität
Sicherheitsäquivalent Risikoprämie Null
gleich
Lineare Nutzenfunktion
Erwartungswert
Beispiel




Ein Landwirt überlegt, ob er Weizen oder Erdbeeren anbauen soll.
(Alternativen ai)
Sein Ziel ist Gewinnmaximierung (Z).
Entscheidender Umfeldzustand ist das Wetter. Er kann die Eintrittswahrscheinlichkeiten für die Uj schätzen.
Er hat für jede Alternative und jeden Umfeldzustand eine Ergebnisfunktion,
kann also die eij (Gewinne) prognostizieren.
Wetter
heiß/trocken
W = 0,1
mild/trocken
W = 0,3
mild/feucht
W = 0,6
Weizen
1.600
3.600
10.000
Erdbeeren
12.100
8.100
6.400
Beispiel



Der Landwirt hat die Risiko-Nutzen-Funktion RNF (eij) = √eij
Daraus ergibt sich die Nutzenmatrix und der Erwartungsnutzen.
Da der Erwartungsnutzen für die Erdbeeren höher ist, wählt er die
Erdbeeren.
Wetter
heiß/trocken
0,1
mild/trocken
0,3
mild/feucht Erwartungsnutzen
0,6
Weizen
40
60
100
0,1 * 40 + 0,3 * 60 +
0,6 * 100 = 82
Erdbeeren
110
90
80
0,1 * 110 + 0,3 * 90 +
0,6 * 80 = 86
Beispiel



Sein Sicherheitsäquivalent ist der sichere
Betrag, der ihm den gleichen Nutzen bringt wie
die Erdbeeren, also 86. Gesucht ist der Betrag,
der eingesetzt in die RNF genau 86 ergibt.
RNF(SÄ) = 86
√SÄ = 86 | hoch 2
SÄ = 86² = 7.396
Für mindestens 7396 € würde der Landwirt auf
den Anbau verzichten und bspw. das Land
verpachten.
Beispiel



Der Landwirt ist risikoscheu. Der
Erwartungswert des Erdbeeranbaus ist
0,1 * 12.100 + 0,3 * 8.100 + 0,6 * 6400 = 7480.
Das SÄ liegt unter dem Erwartungswert.
Die Risikoprämie ist positiv: 7480 – 7396 = 84.
Die Nutzenfunktion ist konkav.
Kritik



Die meisten Menschen haben keine eindeutige
Risikonutzenfunktion, sondern mischen risikoscheues
und risikofreudiges Verhalten. Sie zahlen bspw.
Versicherungsprämien, die über dem Schadenserwartungswert liegen (risikoscheu) und spielen Lotto
(risikofreudig).
Risikofreude oder –scheu variieren auch mit der Höhe
des Einsatzes und der Vermögensposition. Verluste
werden stärker bewertet als Gewinne.
Wahrscheinlichkeiten werden nicht linear bewertet. Eine
Steigerung von 0,98 auf 1 wird viel stärker positiv
gewertet als eine Steigerung von 0,02 auf 0,05.