Diagnose und Prognose: Kurzfassung 4

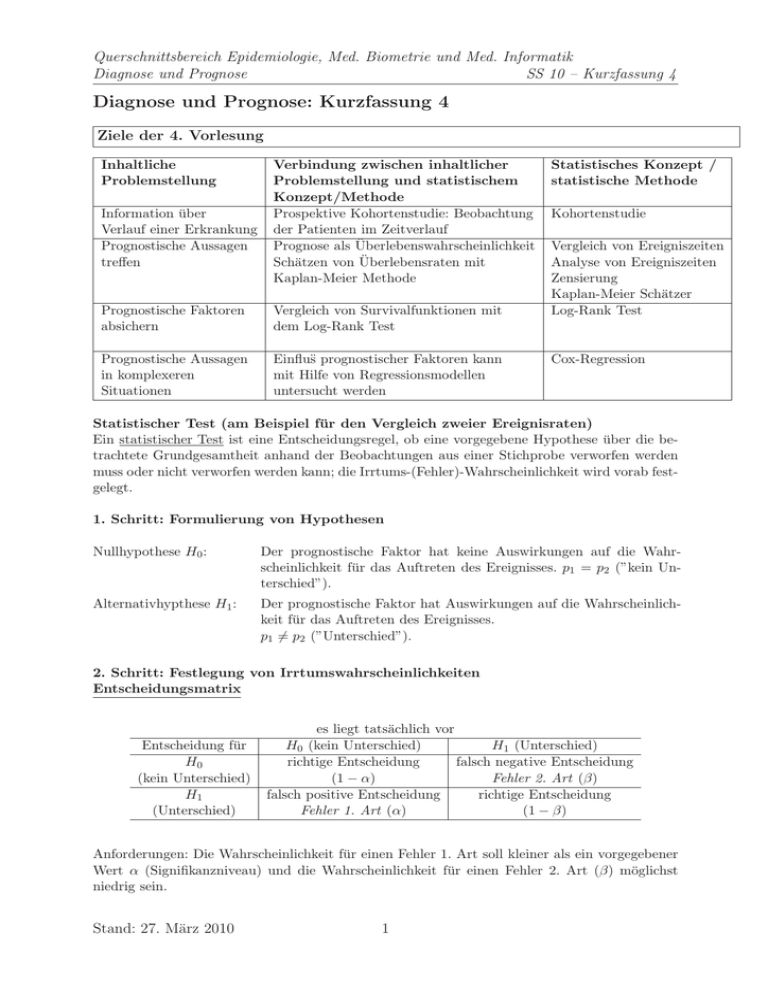
Querschnittsbereich Epidemiologie, Med. Biometrie und Med. Informatik
Diagnose und Prognose
SS 10 – Kurzfassung 4
Diagnose und Prognose: Kurzfassung 4
Ziele der 4. Vorlesung
Inhaltliche
Problemstellung
Information über
Verlauf einer Erkrankung
Prognostische Aussagen
treffen
Verbindung zwischen inhaltlicher
Problemstellung und statistischem
Konzept/Methode
Prospektive Kohortenstudie: Beobachtung
der Patienten im Zeitverlauf
Prognose als Überlebenswahrscheinlichkeit
Schätzen von Überlebensraten mit
Kaplan-Meier Methode
Prognostische Faktoren
absichern
Vergleich von Survivalfunktionen mit
dem Log-Rank Test
Prognostische Aussagen
in komplexeren
Situationen
Einflus̈ prognostischer Faktoren kann
mit Hilfe von Regressionsmodellen
untersucht werden
Statistisches Konzept /
statistische Methode
Kohortenstudie
Vergleich von Ereigniszeiten
Analyse von Ereigniszeiten
Zensierung
Kaplan-Meier Schätzer
Log-Rank Test
Cox-Regression
Statistischer Test (am Beispiel für den Vergleich zweier Ereignisraten)
Ein statistischer Test ist eine Entscheidungsregel, ob eine vorgegebene Hypothese über die betrachtete Grundgesamtheit anhand der Beobachtungen aus einer Stichprobe verworfen werden
muss oder nicht verworfen werden kann; die Irrtums-(Fehler)-Wahrscheinlichkeit wird vorab festgelegt.
1. Schritt: Formulierung von Hypothesen
Nullhypothese H0 :
Der prognostische Faktor hat keine Auswirkungen auf die Wahrscheinlichkeit für das Auftreten des Ereignisses. p1 = p2 (”kein Unterschied”).
Alternativhypthese H1 :
Der prognostische Faktor hat Auswirkungen auf die Wahrscheinlichkeit für das Auftreten des Ereignisses.
p1 6= p2 (”Unterschied”).
2. Schritt: Festlegung von Irrtumswahrscheinlichkeiten
Entscheidungsmatrix
Entscheidung für
H0
(kein Unterschied)
H1
(Unterschied)
es liegt tatsächlich vor
H0 (kein Unterschied)
H1 (Unterschied)
richtige Entscheidung
falsch negative Entscheidung
(1 − α)
Fehler 2. Art (β)
falsch positive Entscheidung
richtige Entscheidung
Fehler 1. Art (α)
(1 − β)
Anforderungen: Die Wahrscheinlichkeit für einen Fehler 1. Art soll kleiner als ein vorgegebener
Wert α (Signifikanzniveau) und die Wahrscheinlichkeit für einen Fehler 2. Art (β) möglichst
niedrig sein.
Stand: 27. März 2010
1
Querschnittsbereich Epidemiologie, Med. Biometrie und Med. Informatik
Diagnose und Prognose
SS 10 – Kurzfassung 4
• Festlegen eines Signifikanzniveaus (etwa α = 5%)
• Verwendung einer geeigneten Prüfgrös̈e, die zu einem möglichst ”mächtigen”
(d.h. 1 − β groß!) statistischen Test führt.
• (1 − β) wird auch Power des statistischen Tests genannt.
3. Schritt: Berechnung einer Prüfgröße (Teststatistik)
T =
p̂1 − p̂2
SE(p̂1 − p̂2 )
mit
p̂1 =
a
a+b
und
p̂2 =
c
c+d
Unter der Nullhypothese H0 : p1 = p2 = p vereinfacht sich die Formel zur Berechnung des
Standardfehlers SE(p̂1 − p̂2 ) zu
s
p̂ (1 − p̂) p̂ (1 − p̂)
(a + c)
SE(p̂1 − p̂2 ) =
+
mit p̂ =
(a + b)
(c + d)
n
4. Schritt: Entscheidungsregel
Falls |T | ≥ kritischer Wert k
Entscheidung
für H1
(”Nullhypothese wird
verworfen”)
Test ist ”signifikant”
Falls |T | < kritischer Wert k
Beibehaltung
von H0
(”Nullhypothese kann
nicht verworfen werden”)
Test ist ”nicht signifikant”
Der kritische Wert k wird so gewählt, dass die Wahrscheinlichkeit für den Fehler 1. Art kleiner
oder gleich dem vorgegebenen Signifikanzniveau ist (z.B. k = 1, 96 für α = 5%.)
p-Wert (”Überschreitungswahrscheinlichkeit”): gibt bei einem statistischen Test die Wahrscheinlichkeit an, mit der sich unter der Nullhypothese für die Prüfgröße Werte größer oder gleich
dem beobachteten Wert einstellen können.
Ist der p-Wert kleiner als das festgelegte Signifikanzniveau, wird die Nullhypothese verworfen
(Entscheidung für H1 ).
Dualität von statistischem Test und Konfidenzintervall
Einen statistischen Test zum Signifikanzniveau α kann man auch in der Weise durchführen, indem man prüft, ob der unter der Nullhypothese angenommene Wert einer statistischen Mas̈zahl
im jeweiligen (1 − α)-Konfidenzintervall enthalten ist.
Analyse von Überlebenszeiten
• Einbeziehung von zensierten Beobachtungen
• Schätzung von Überlebenswahrscheinlichkeiten nach Kaplan-Meier
• Logrank-Test zum Vergleich von Überlebenskurven
• Cox-Modell als Multivariables Regressionsmodell für Überlebenszeiten analog zur logistischen Regression für dichotome Daten
Stand: 27. März 2010
2
Querschnittsbereich Epidemiologie, Med. Biometrie und Med. Informatik
Diagnose und Prognose
SS 10 – Kurzfassung 4
Schematische Darstellung eines typischen Ablaufs einer klinischen Studie:
◦
Zeitpunkt der Aufnahme in die Studie
⊣ Ereigniszeitpunkt
→ Zeitpunkt des letzten Kontakts (zensierte Beobachtung)
T Zeit bis zum Ereignis bekannt
A Zensierung aus administrativen Gründen (Studienende)
L Zensierung aus anderen Gründen (Lost to Follow Up)
6◦
T
-
5◦
4◦
T
-
3◦
A
L
-
2◦
1◦
A
T
-
1996
Rekrutierungsperiode
(1996–2000)
Kalenderzeit
2000 Nachbeobachtung 2003
(2000–2003)
Studienende
Schätzung von Überlebenswahrscheinlichkeit S(t) (Kaplan-Meier-Schätzer)
Survival Funtion S(t)
S(t) = Wahrscheinlichkeit bis zum Zeitpunkt t zu überleben. Ein Beispieldatensatz
Überlebeszeit
(in Monaten)
5
7
10
12
13
17
20
Status
tot
tot
tot
zensiert
tot
zensiert
zensiert
Kaplan–Meier Kurve
Bei jedem Ereignis (Tod) fällt die Kaplan-Meier-Kurve um 1/n. Zensierte Beobachtungen werden
auf alle zuküngtigen Ereignisse verteilt. Dadurch wird der Abfall der Kurve bei einem Ereignis
entsprechend größer.
Die Kaplan-Meier Kurve erlaubt zu jedem Zeitpunkt t die geschätzte Wahrscheinlichkeit des
Überlebens bis zum Zeitpunkt t abzulesen. Z.B können wir ablesen, dass die geschätzte Wahrscheinlichkeit 8 Monate zu überleben 71% beträgt.
Stand: 27. März 2010
3
Querschnittsbereich Epidemiologie, Med. Biometrie und Med. Informatik
Diagnose und Prognose
SS 10 – Kurzfassung 4
100%
75%
50%
25%
0%
0
3
6
9
12
months
15
18
21
Vergleich von zwei Überlebenszeitverteilungen (Logrank-Test)
• Betrachte 2 Gruppen von Patienten (A und B)
• SA (t) und SB (t) wahre Überlebensfunktionen von Gruppe A bzw. B
Testproblem:
H0 : “Die Überlebensfunktionen sind gleich” gegen H1 : “Die Überlebensfunktionen unterscheiden
sich”.
mathematisch:
H0 : SA (t) = SB (t) für alle t
vs.
H1 : SA (t) 6= SB (t) für alle t
Cox–Regression (für zensierte Überlebenszeiten)
Hazard Ratio (von FaktorXj )
= um wieviel steigt die Wahrscheinlichkeit an einem beliebigen Zeitpunkt t zu sterben, (gegeben
man hat bis zum Zeitpunkt t überlebt), wenn wirXj um 1 erhöhen ?
Typische Beispiele:
HR(Therapie A vs.Therapie B)=0.8
→ Risiko zu sterben ist unter Therapie A um den Faktor 0.8 kleiner
HR(Alter)=1.02 → Risiko zu sterben wächst mit jedem Jahr um 1.02
prognostische und prädiktive Faktoren
prognostische Faktoren: Erlauben, die Prognose (Überlebenswahrscheinlichkeit) eines Patienten
zu bestimmen.
prädiktive Faktoren: Erlauben, einen Therapiererfolg vorherzusagen.
Lernziele der Vorlesung
Stand: 27. März 2010
4
Querschnittsbereich Epidemiologie, Med. Biometrie und Med. Informatik
Diagnose und Prognose
SS 10 – Kurzfassung 4
1. Prognostische Fragestellungen werden typischerweise in prospektiven Kohortenstudien untersucht. Dabei werden Patienten im Zeitverlauf bis zum Eintreten eines interessierenden
Ereignisses beobachtet.
2. Prognose kann als Wahrscheinlichkeit angegeben werden, dass das interessierende Ereignis
zu einem Zeitpunkt eingetreten ist: Statistischer Test zum Vergleich von Ereignisraten.
3. Die spezielle Datenstruktur (Zensierungen) erfordert eine spezielle Methodik (KaplanMeier Schätzung).
4. Methoden für komplexere Fragestellungen: Log-Rank Test, Cox Modell.
5. Die Interaktion prognostischer Faktoren mit einer Therapie kann in prospektiv geplanten
Analysen untersucht werden.
6. Der Einfluss prognostischer Faktoren kann in Regressionsmodellen untersucht werden.
Im Cox-Modell können die Parameter als Relative Risiken (Hazard Ratios) interpretiert
werden.
Tabelle der Verteilungsfunktion der Standardnormalverteilung
Stand: 27. März 2010
z
0.000
0.126
0.253
0.385
0.524
Φ(z)
0.5
0.55
0.6
0.65
0.7
Φ(−z)
0.5
0.45
0.4
0.35
0.3
0.674
0.842
1.036
1.282
1.645
0.75
0.8
0.85
0.9
0.95
0.25
0.2
0.15
0.1
0.05
1.960
2.054
2.326
2.576
2.878
0.975
0.98
0.99
0.995
0.998
0.025
0.02
0.01
0.005
0.002
3.090
3.291
3.540
3.749
∞
0.999
0.9995
0.9998
0.9999
1.0000
0.001
0.0005
0.0002
0.0001
0.000
5