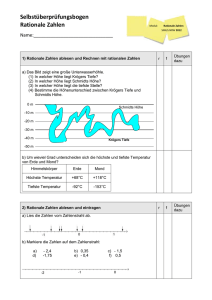
Einstieg: Rationale Zahlen subtrahieren

Name:
Klasse:
Datum:
Einstieg: Rationale Zahlen subtrahieren
Rationale Zahlen subtrahieren
1 Berechne 2,5 – 1,5 und 2,5 – (– 1,5) mithilfe der beiden Abbildungen.
2,5 – 1,5 =
2,5 – (– 1,5)=
© 2014 Cornelsen Schulverlage GmbH, Berlin.
Alle Rechte vorbehalten.
a) Vergleiche die beiden Vorgehensweisen und formuliere eine Regel, wie man rationale
Zahlen subtrahiert.
b) Berechne –2,5 – 1,5 und –2,5 – (–1,5). Zeichne den Lösungsweg mithilfe einer
Zahlengeraden und notiere das Ergebnis.
–2,5 –1,5 =
–2,5 – (– 1,5) =
2 Schreibe erst als Additionsaufgabe und berechne dann die Aufgaben.
a) 3 – (–2,5) =
b) –45 – (+1,3) =
1
1
c) 4 – –2 =
Didaktische Erläuterungen
Einstieg: Rationale Zahlen subtrahieren
Rationale Zahlen subtrahieren
Vorwissen:
Subtraktion natürlicher Zahlen
Material:
Arbeitsblatt
© 2014 Cornelsen Schulverlage GmbH, Berlin.
Alle Rechte vorbehalten.
Lernziel:
Die Schülerinnen und Schüler subtrahieren zwei rationale Zahlen mit gleichen und
unterschiedlichen Vorzeichen.
Methodische Hinweise:
Die Subtraktion rationaler Zahlen wird mithilfe des Modells des Pfeils an einer Zahlengera–
den dargestellt. Indem die Schülerinnen und Schüler die beiden Vorgehensweisen für das
Subtrahieren einer positiven und einer negativen Zahl von einer positiven Zahl vergleichen
und die Orientierung des Pfeils in entgegengesetzte Richtungen vor Augen haben, können sie
das Prinzip der Addition der Gegenzahl erschließen.
Diese Vorgehensweise wird nochmals verschriftlicht (Aufgabe 1a), um sicherzustellen, dass
das Prinzip verstanden worden ist. Anschließend kann das Verfahren auf das Subtrahieren
einer positiven und negativen Zahl von einer negativen Zahl selbstständig übertragen werden
(Aufgabe 1b). Durch das Einzeichnen der Pfeile wird wiederum das Addieren der Gegenzahl
visualisiert, bevor konkret gerechnet wird.
Nach der selbstständigen Erarbeitungsphase wird das Verfahren und die Formulierung einer
allgemeinen Regel im Klassenverband besprochen.
Abschließend erfolgt die Anwendung in Aufgabe 2 und die Subtraktion von rationalen Zahlen
wird anhand weiterer Beispiele geübt.
Wie in den Lerneinheiten 2.1 und 2.2 kann auch hier das Verfahren mithilfe anderer Modelle
visualisiert werden. Dazu können Streifenbildern und Zahlengeraden als Vorlagen zum
Ausschneiden zur Verfügung gestellt werden
Einbettung in Buchkontext: Wissen: „Subtrahieren rationaler Zahlen“
Mögliche Stundenskizze:
Arbeitsblatt Aufgabe 1a) – b) (Einzelarbeit/Partnerarbeit) (15-20 Minuten)
Sicherung: „Rationale Zahlen subtrahieren“ (5-10 Minuten)
Übung: Arbeitsblatt Aufgabe 2 (Einzelarbeit) (10-15 Minuten)
Hausaufgabe: Aufgaben 1 und 2 im Buch
Lösung
Einstieg: Rationale Zahlen subtrahieren
Rationale Zahlen subtrahieren
1 Berechne 2,5 – 1,5 und 2,5 – (– 1,5) mithilfe der beiden Abbildungen.
2,5 – 1,5 = 1
2,5 – (–1,5 ) = 4
a) Vergleiche die beiden Vorgehensweisen und formuliere eine Regel, wie man rationale
Zahlen subtrahiert.
© 2014 Cornelsen Schulverlage GmbH, Berlin.
Alle Rechte vorbehalten.
Subtrahiert man eine positive Zahl, so geht man auf der Zahlengeraden
nach links. Subtrahiert man eine negative Zahl, so geht man auf der
Zahlengeraden nach rechts.
Allgemein gilt: Man subtrahiert eine rationale Zahl, indem man die
entgegengesetzte Zahl addiert.
b) Berechne –2,5 – 1,5 und –2,5 – (–1,5). Zeichne den Lösungsweg mithilfe einer
Zahlengeraden und notiere das Ergebnis.
–2,5 –1,5 = –4
–2,5 – (–1,5) = –1
2 Schreibe erst als Additionsaufgabe und berechne dann die Aufgaben.
a) 3 – (–2,5) = 3 + 2,5 = 5,5
b) –45 – (+1,3) = –45 + (–1,3) = –46,3
 1 1
2
3
1
 1 1
c) 4 – –2 =
+ +  = +
=
  4
4
4
 2 4