1_9_Gase
Werbung

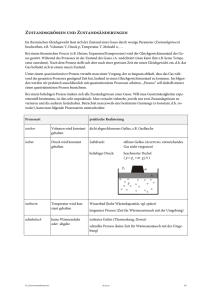
Ideale Gase Ideale Gase sind ein „Modellsystem“: - kugelförmige Teilchen, frei beweglich - Wechselwirkung nur durch vollkommen elastische Stöße (Energieübertrag ändert nur die kinetische Energie; keine inneren Anregungen) - mittlere Geschwindigkeit der Teilchen bestimmt die Temperatur Gase nehmen jeden verfügbaren Raum ein; die Größe dieses Raums ist abhängig vom Druck im Gas vom Druck aus der Umgebung; die Größe dieses Raums bestimmt die Dichte: druckabhängige Dichte; 1 Modellvorstellung zum Druck Druck entsteht durch den Stoß der Gasteilchen an die Gefäßwand: makroskopisch gemessener Druck ist Summe vieler Teilchenstöße jeder Teilchenstoß ist ein Impulsübertrag an die Wand, die den doppelten Gegenimpuls aufnimmt [Teilchenimpuls vor dem Stoß: p1 = mv1 Teilchenimpuls nach dem Stoß : p2 = m(-v1) , also Impulsübertrag Dp = p2 – p1 = -2mv1 ] Häufigkeit der Impulsüberträge Dp auf die Wand bestimmt Druckwirkung: Je mehr Teilchen pro Zeiteinheit die Wand treffen, desto höher der Druck. 2 Gasgesetze I Gesetz von Amontons (1663-1705) : Druckänderung bei konstantem Volumen Gasvolumen mit bestimmtem Druck erwärmen, Manometer ausgleichen und aus dem Schweredruck der überstehenden Flüssigkeit den Druck im Gasvolumen bestimmen: p =p1+p2 =Luftdruck + rFl·g·Dh 3 Gasgesetze II Gesetz von Gay-Lussac (1778-1850) : Volumenänderung bei konstantem Druck Gasvolumen erwärmen, die aufsteigende Gasmenge in einem Auffangbehälter messen,der im Druckgleichgewicht mit der Umgebungsluft steht. Buch „Newton“, Physik 9 I-III V = V0 +DV 4 Gasgesetze III Gesetz von Boyle (1627-1691) -Mariotte (1620-1684) : Änderung von Druck und Volumen bei konstanter Temperatur Beispiel: langsame Druckänderung in einer Fahrradpumpe P · V = const. , bei konstanter Temperatur (V = Weg l x Querschnittsfläche A) (Film zeigen) 5 Ideale Gasgleichung Kombination der drei Gasgesetze: - von Amontons: p/T = const bei konstantem Volumen - von Gay-Lussac: V/T = const bei konstantem Druck - von Boyle-Mariotte: p*V = const bei konstanter Temperatur ergibt eine Gleichung, die alle Variablen eines Gaszustandes enthält: Betrachte die Abfolge der beiden Zustandsänderungen zwischen 3 Zuständen ! Buch „Newton“, Physik 9 I-III 6 Allgemeine Gaskonstante P V const. Der Wert der Konstanten ist abhängig vom Teilchengehalt des Gases. Für eine Teilchenzahl n gilt: P V n R R ist die allgemeine Gaskonstante bei Normalbedingungen ( V = 22,4 l, p = 1013 hPa, T = 273.15 K, n = 1mol) ist R = 8,314 J / (mol·K) Gase 7 Ideales und reales Gas P,V – Zustandsdiagramm in Kohlendioxid Experiment Theorie van der Waals (1837-1923): (p a V 2 )(V b) n R Gleichung 3. Grades im Volumen V 8 Eigenschaften realer Gase Im realen Gas gibt es eine Wechselwirkung zwischen den Gasteilchen: van der Waals – Kräfte (gegenseitig induzierte elektrische Dipole in den Elektronenhüllen zweier Teilchen) praktische Folgen: Koexistenzphase zwischen verschiedenen Aggregatszuständen Verflüssigung durch Temperatur-/Druckänderung bei genügend hohen Temperaturen verhält sich ein reales Gas wie das ideale Gas Gase 9 Allgemeine Gaskonstante R ist ein Maß für die Energie eines Mols eines Gases: R = 8,314 J / (mol · K) Teilt man diesen Wert durch die Anzahl der Teilchen eines Mols eines Stoffes ( n = 6,022 · 10 23 ), so erhält man die Energiemenge pro Teilchen: kB = R/n = 1,38 * 10 -23 J/K kB heißt Boltzmann(1844-1906)-Konstante und gibt die Energiemenge an, die ein Gasteilchen bei einer Temperaturänderung pro K zugeführt bekommt bzw. abgibt. Daraus ergibt sich die kinetische Energie der Gasteilchen: m·v²/2 = 3/2 · kB · T, wobei v die mittlere Geschwindigkeit der Gasteilchen ist. 10 Zustandsänderungen des idealen Gases Die Gasgleichung beschreibt die Änderung des Energiezustandes in einem idealen Gas: V/ = const: isobare Zustandsänderung: p/ = const: isochore Zustandsänderung p·V = const: isotherme Zustandsänderung P V n R Beim letzten Beispiel ist am einfachsten anschaulich zu machen, dass all diese Prozesse mit einem Energieaustausch mit der Umgebung verbunden sind (Warmwerden der Fahrradpumpe). (Findet kein Energieaustausch mit der Umgebung statt, so heißt die Zustandsänderung „adiabatisch“ DQ = 0 = DW + ΔU DW = - ΔU) Gase 11 Energieumsatz in Gasen Einheitenbetrachtung: [p]=1N/m²; [V]=1m³; [p]*[V] = 1Nm = [E] isochor isobar isotherm schraffierte Fläche: mechanischer Energieumsatz ( Arbeit! ) Gase 12