Kapitel 6: Stetige Verteilungen

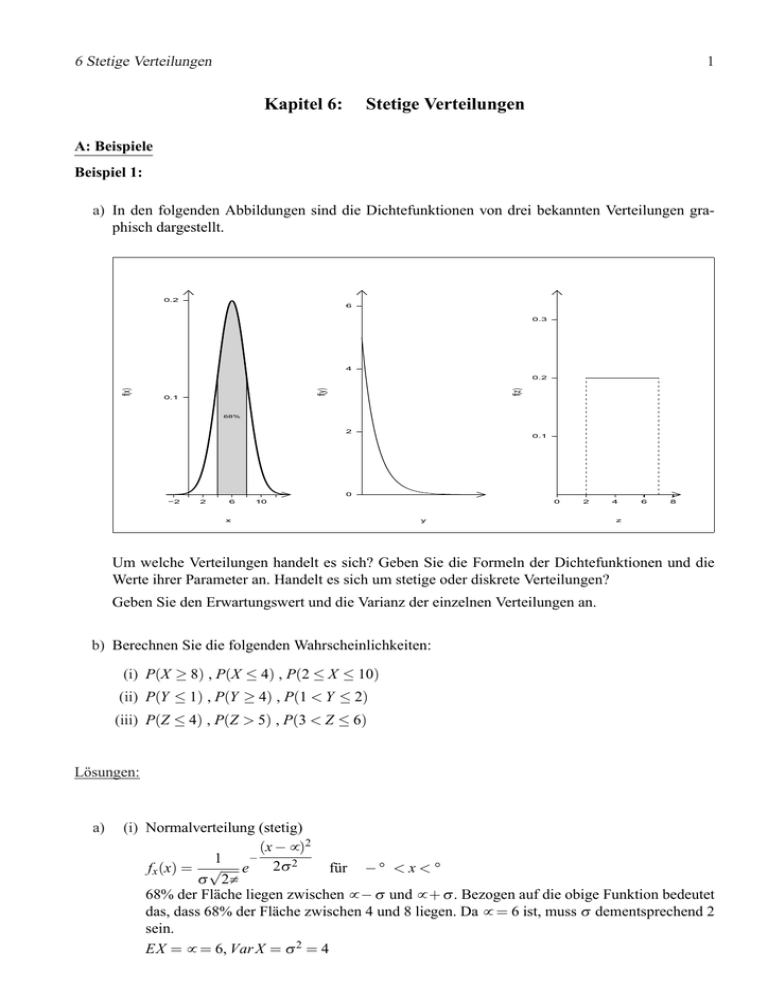
6 Stetige Verteilungen
1
Kapitel 6:
Stetige Verteilungen
A: Beispiele
Beispiel 1:
a) In den folgenden Abbildungen sind die Dichtefunktionen von drei bekannten Verteilungen graphisch dargestellt.
0.2
6
0.3
4
0.1
f(z)
f(y)
f(x)
0.2
68%
2
0.1
0
−2
2
6
10
x
0
2
y
4
6
8
z
Um welche Verteilungen handelt es sich? Geben Sie die Formeln der Dichtefunktionen und die
Werte ihrer Parameter an. Handelt es sich um stetige oder diskrete Verteilungen?
Geben Sie den Erwartungswert und die Varianz der einzelnen Verteilungen an.
b) Berechnen Sie die folgenden Wahrscheinlichkeiten:
(i) P(X ≥ 8) , P(X ≤ 4) , P(2 ≤ X ≤ 10)
(ii) P(Y ≤ 1) , P(Y ≥ 4) , P(1 < Y ≤ 2)
(iii) P(Z ≤ 4) , P(Z > 5) , P(3 < Z ≤ 6)
Lösungen:
a)
(i) Normalverteilung (stetig)
(x − µ )2
−
1
2σ 2
fx (x) = √ e
für − ∞ < x < ∞
σ 2π
68% der Fläche liegen zwischen µ − σ und µ + σ . Bezogen auf die obige Funktion bedeutet
das, dass 68% der Fläche zwischen 4 und 8 liegen. Da µ = 6 ist, muss σ dementsprechend 2
sein.
EX = µ = 6, Var X = σ 2 = 4
6 Stetige Verteilungen
2
(ii) Exponentialverteilung (stetig)
½
−λ y
für y ≥ 0
fy (y) = λ e
0
sonst
mit λ = 5
1
1
E Y = , VarY = 2
λ
λ
(iii) Rechteckverteilung (stetig)

 1
für a ≤ z ≤ b
fz (z) = b − a

0
sonst
mit a = 2 ; b = 7
EZ =
(b − a)2
a+b
, Var Z =
2
12
µ
b)
¶
8−6
(i) P(X ≥ 8) = 1 − P(X ≤ 8) = 1 − Φ
= 1 − Φ(1) = 0.159
2
µ
¶
4−6
P(X ≤ 4) = Φ
= Φ(−1) = 0.159
2µ
¶
µ
¶
10 − 6
2−6
P(2 ≤ X ≤ 10) = Φ
−Φ
= Φ(2) − Φ(−2) = 0.954
2
2
·
Z1
(ii) P(Y ≤ 1) = 5 ·
e
0
−5y
1
dy = 5 · − · e−5y
5
−5y
e
·
Z2
e
1
Z4
(iii) P(Z ≤ 4) =
2
Z7
P(Z > 5) =
5
µ ¶ ¶
1 −5·1
1
= 5· − ·e
− −
· e0 = 0.993
5
5
0
1
dy = 1 − 5 · − · e−5y
5
0
P(1 < Y ≤ 2) = 5 ·
µ
·
Z4
P(Y ≥ 4) = 1 − 5 ·
¸1
−5y
1
dy = 5 · − · e−5y
5
¸4
µ
µ ¶ ¶
1 −20
1
= 1−5· − ·e
− −
· e0 = 0
5
5
0
¸2
µ ¶
¶
1 −10
1
−5
= 5· − ·e
− −
·e
= 0.007
5
5
1
·
¸4
1
1
1
1
2
dz =
·z = ·4− ·2 =
5
5
5
5
5
2
·
¸7
1
1
1
1
2
dz =
·z = ·7− ·5 =
5
5
5
5
5
5
Z6
P(3 < Z ≤ 6) =
3
·
¸6
1
1
1
1
3
dz =
·z = ·6− ·3 =
5
5
5
5
5
3
µ
6 Stetige Verteilungen
3
B: Übungsaufgaben
[1]
Die folgenden Aussagen betreffen die Familie der Exponentialverteilungen. Welche der folgenden
Aussagen sind WAHR? Kreuzen Sie diese an.
a)
Die Verteilung einer exponentialverteilten Zufallsvariablen ist erst dann völlig festgelegt, wenn außer dem Parameter λ auch die Varianz bekannt ist.
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
b) Eine exponentialverteilte Zufallsvariable ist stetig.
(
)
c)
Man benutzt exponentialverteilte Zufallsvariablen als Modell für die Wartezeiten zwischen dem Eintreten zweier Ereignisse.
(
)
d) Der Parameter λ einer Exponentialverteilung kann alle Werte zwischen −1 und +1
annehmen.
(
)
(
)
b) Die Exponentialverteilung hat einen Parameter λ und für diesen gilt λ = 1/EX > 0.
c)
Für alle Dichten aus der Familie der Exponentialverteilungen gilt f (0) = 1.
d) Vergrößert man den Parameter λ , so vergrößert sich auch der Erwartungswert.
e)
Vergrößert man den Wert des Parameter λ , so werden mehr kleine Werte angenommen.
[2]
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
Für eine normalverteilte Zufallsvariable gilt immer:
a)
Der Erwartungswert ist gleich der Varianz.
b) Eine normalverteilte Zufallsvariable mit µ = 0 und σ 2 = 1 nennt man standardnormalverteilt.
c)
P(X ≤ µ ) = 0.5.
d) Die Dichtefunktion ist symmetrisch zur Geraden x = 0.
e)
Die Dichtefunktion hat an der Stelle µ ihr Maximum.
[3]
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie diese an.
a)
e)
Die Exponentialverteilung hat die Dichte
λ x −λ
, x ≥ 0.
x! e
Für die Dichte einer Exponentialverteilung gilt f (x) > 0 für alle x ∈ (−∞, ∞).
6 Stetige Verteilungen
4
[4]
Die Dichtefunktion
2
1
f (x) = √ e−0.25x −x−1
2 π
beschreibt eine Normalverteilung N(µ , σ 2 ).
Bestimmen Sie die Parameter µ und σ 2 .
µ =
σ =
f(x)
[5]
Gegeben sei folgende Normalverteilung:
68.2%
0
1
2
3
4
5
6
7
x
Berechnen Sie folgende Wahrscheinlichkeiten:
P(X ≥ 3) =
P(X ≤ 3) =
P(X ≥ 5) =
6 Stetige Verteilungen
5
[6]
f(x)
0.2
0.1
10
b
x
Die Dichtefunktion einer rechteckverteilten Zufallsvariablen X ist oben gezeichnet. Bestimmen Sie:
a)
b
=
f)
P(X ≤ 15)
=
b)
P(X > b)
=
g)
P(12 ≤ X ≤ 14)
=
c)
P(X ≤ b)
=
h)
P(X > 16)
=
µ
d)
EX
=
e)
Var X
=
i)
j) F(x) =
10 + b
P X≤
2
für
¶
=
6 Stetige Verteilungen
6
[7]
Die Zufallsvariable X sei N(0; 1) - verteilt. Es gilt P(X ≥ a) = 0.115. Geben Sie den Wert für a an.
a=
f(x)
[8]
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
A
0
a
x
Bei der N(0, 1) - Verteilung ist A die Wahrscheinlichkeit des Intervalls (0, a). Wenn X eine N(0, 1) verteilte Zufallsvariable ist, dann ist:
P(X > a) = 1 − A
(
)
b) P(−a < X < a) = 2A
(
)
P(X < a) = 0.5 − A
(
)
d) P(X ≤ −a) = P(X > a)
(
)
P(X < a) = 0.5 + A
(
)
a)
c)
e)
6 Stetige Verteilungen
7
[9]
Die Zufallsvariable X sei normalverteilt mit EX = µ und Var X = σ 2 .
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
E (X − µ ) = 0
(
)
b) Var (X − µ ) = 0
µ
¶
X −µ
c) Var
=1
σ
¶
µ
X −µ
d) E
=0
σ
(
)
(
)
(
)
(
)
a)
e)
Var X = Var(X − µ )
[ 10 ]
Eine Zufallsvariable X sei N(0; 1) - verteilt.
Für welches a gilt: P(−a ≤ X ≤ a) = 0.874
a=
[ 11 ]
Die Zufallsvariable X sei normalverteilt mit den Parametern µ = 25 und σ 2 = 16.
Berechnen Sie folgende Wahrscheinlichkeiten:
a)
P(21 ≤ X ≤ 57)
=
c)
P(X > 37)
=
b)
P(17 ≤ X ≤ 33)
=
d)
P(X ≤ 21)
=
[ 12 ]
Sei X normalverteilt mit µ = 4 und σ = 2.
Bestimmen Sie die folgenden Wahrscheinlichkeiten:
a)
P(2 ≤ X ≤ 6) =
b)
P(X ≤ 3) =
c) P(3 ≤ X ≤ 5) =
d)
P(X ≥ 6) =
6 Stetige Verteilungen
8
f(x)
[ 13 ]
Gegeben sei folgende Normalverteilung:
B
A
µ−σ µ µ+σ
x
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an. (Nutzen Sie gegebenenfalls die
Tabelle.)
a)
0.5 − A = B
(
)
b)
f (µ − σ ) = f (µ + σ )
(
)
c)
P(X < µ ) = 0.5
(
)
(
)
(
)
d) P(X < µ + σ ) = 1 − 2B
e)
A = 0.159
[ 14 ]
Die Zeit in Minuten zwischen den Ankünften zweier Fußgänger an einem ampelgesteuerten Zebrastreifen sei exponentialverteilt mit einem Erwartungswert von 1.25 Minuten.
Mit welcher Wahrscheinlichkeit verstreichen mehr als 2 Minuten zwischen den Ankünften zweier
Fußgänger?
P(X > 2) =
6 Stetige Verteilungen
9
[ 15 ]
Die Zufallsvariable X sei normalverteilt mit µ = 100 und VarX = σ 2 . Es gilt P(X ≤ 110) = 0.788.
Berechnen Sie die Standardabweichung σ der Zufallsvariablen X.
σ =
[ 16 ]
Eine Zufallsvariable X sei normalverteilt mit µ = 10. Außerdem gelte P (5 ≤ X ≤ 15) = 0.9544.
Bestimmen Sie daraus die Standardabweichung der Zufallsvariablen X .
σ =
[ 17 ]
Die Zufallsvariable X sei normalverteilt mit den Parametern µ = 12 und σ 2 = 16.
Für welches a gilt P(µ − a ≤ X ≤ µ + a) = 0.866.
a=
[ 18 ]
Eine Zufallsvariable Y sei exponentialverteilt mit λ = 2. Bestimmen Sie f (0), den Wert der Dichtefunktion an der Stelle Y = 0, und die folgenden Wahrscheinlichkeiten:
a)
f(0)
=
µ
¶
1
d) P Y ≤
2
b)
P(Y ≥ 0)
=
e)
µ
c)
1
<Y ≤2
P
2
¶
=
P(Y > 2)
=
=
6 Stetige Verteilungen
10
[ 19 ]
Für eine normalverteilte Zufallsvariable X mit Erwartungswert µ und Varianz σ 2 gelte f (x) = f (−x)
und P(X ≤ 2) = 0.841.
a) Bestimmen Sie die Wahrscheinlichkeit P(−1 < X < 0).
P(−1 < X < 0) =
b) Geben Sie den entsprechenden R–Befehl an.
R–Befehl =
[ 20 ]
Das Eingehen von Telefonanrufen in einem Call–Center aus Beispiel 1.10 wird durch einen Poissonprozess beschrieben. Im Durchschnitt gehen in 1000 Sekunden 7 Anrufe ein.
a) Bestimmen Sie den Parameter λ und berechnen Sie die Wahrscheinlichkeit, dass die Zeit, die
zwischen zwei Anrufen vergeht, mindestens 6 Minuten beträgt.
P(X ≥ 6) =
b) Geben Sie den entsprechenden R–Befehl an.
R– Befehl =
6 Stetige Verteilungen
11
[ 21 ]
Betrachten Sie Beispiel 1.7 aus dem Skript. Das Zeitintervall zweier Erdbeben der Stärke 7.0 oder
größer sei exponentialverteilt mit einem Erwartungswert von 25 Tagen.
Ihnen sei folgende R–Ausgabe gegeben. (lam ist der Parameter der Verteilung)
Geben Sie das Ergebnis auf 4 Stellen gerundet an.
> round(pexp(0:20,rate=lam),digits=4)
[1] 0.0000 0.0392 0.0769 0.1131 0.1479 0.1813 0.2134
[8] 0.2442 0.2739 0.3023 0.3297 0.3560 0.3812 0.4055
[15] 0.4288 0.4512 0.4727 0.4934 0.5132 0.5323 0.5507
Bestimmen Sie folgende Wahrscheinlichkeiten mit Hilfe der obigen R–Ausgabe.
P(X ≥ 3) =
P(8 ≤ X ≤ 11) =
P(X < 10) =
[ 22 ]
Die Blockzeiten der American Airlines Flüge von Dallas/ Fort Worth nach Philadelphia aus Bespiel
1.2 seit normalverteilt mit den Parametern µ = 183 Minuten und σ 2 = 196 Minuten2 . Geben Sie das
Ergebnis auf 4 Stellen gerundet an.
> round(pnorm(170:196,183,13),digits=4)
[1] 0.1587 0.1780 0.1987 0.2209 0.2444 0.2692 0.2951
[8] 0.3222 0.3503 0.3792 0.4087 0.4389 0.4693 0.5000
[15] 0.5307 0.5611 0.5913 0.6208 0.6497 0.6778 0.7049
[22] 0.7308 0.7556 0.7791 0.8013 0.8220 0.8413
Bestimmen Sie folgende Wahrscheinlichkeiten mit Hilfe der obigen R–Ausgabe.
P(X < 173) =
P(X ≥ 192) =
P(180 ≤ X ≤ 185) =
6 Stetige Verteilungen
12
[ 23 ]
Die Zufallsvariable X sei normalverteilt mit X ∼ N(µ ; σ 2 ).
Welche der folgenden Aussagen sind WAHR ? Kreuzen Sie sie an.
a)
Je kleiner man σ 2 wählt, desto flacher wird die Dichtefunktion.
(
)
(
)
(
)
(
)
(
)
(
)
b) Die t–Verteilung konvergiert mit wachsenden Freiheitsgraden gegen die Normalverteilung.
(
)
Insbesondere für kleine ν ist die Varianz der t–Verteilung größer als die Varianz der
Standardnormalverteilung.
(
)
d) Die F–Verteilung besitzt zwei Parameter, die mit ν1 und ν2 bezeichnet werden.
(
)
e)
(
)
b) P(X < µ ) = 0.5
c)
P(X = 2) = 0
d) Eine Änderung von µ bewirkt eine Verschiebung der Dichtefunktion entlang der xAchse.
e)
P(X − 2σ < X < X + 2σ ) ≈ 0.95
[ 24 ]
Welche der folgenden Aussagen sind in diesem Zusammenhang WAHR ?
Kreuzen Sie sie an.
a) Eine χ 2 –verteilte Zufallsvariable nimmt nur Werte ≥ 0 an.
c)
Die log–Normalverteilung ist gut geeignet, Einkommensverteilungen zu beschreiben.
[ 25 ]
Eine Maschine produziert laufend Werkstücke mit einem Ausschußanteil von 20% . Es werden zufällig 400 Stücke gezogen.
Mit welcher (angenäherten) Wahrscheinlichkeit hat man dabei mehr als 80 Ausschußstücke beobachtet?
(HINWEIS: Nähern Sie die hier zu verwendende diskrete Verteilung durch eine stetige Verteilung an
deren Approximation sich mit Hilfe des Zentralen Grenzwertsatzes ergibt.)
P (X ≥ 800) =
6 Stetige Verteilungen
13
[ 26 ]
Approximieren Sie die Binomialverteilung b (X, n = 100, π = 0.5) durch eine Normalverteilung und
berechnen Sie P (46 ≤ X ≤ 54) mit Hilfe der Stetigkeitskorrektur.
P (46 ≤ X ≤ 54) =
Die exakte Wahrscheinlichkeit lautet: 0.6317984. Sie lässt sich sowohl mit Hilfe der Wahrscheinlichkeitsfunktion als auch mit der Verteilungsfunktion berechnen. Geben Sie die entsprechenden R–
Befehle an:
R–Befehl =
R–Befehl =
[ 27 ]
Die Zufallsvariable X sei hypergeometrisch verteilt mit n = 16 , Ne = 100 , Nm = 300. Approximieren
Sie diese Verteilung zunächst durch eine Binomialverteilung und dann durch eine Normalverteilung.
Überprüfen Sie, ob die Regeln, die in der Vorlesung behandelt wurden, erfüllt sind.
Geben Sie zunächst die Parameter der approximierten Binomialverteilung an:
n=
π =
Geben Sie nun die Parameter der approximierten Normalverteilung an:
µ =
σ =
6 Stetige Verteilungen
C: Klausuraufgaben
[ 28 ] II07S
Die Zufallsvariable X beschreibe das Gewicht von “500 g”-Mehlpackungen und sei normalverteilt
mit dem Erwartungswert µ = 500 und der Varianz σ 2 = 9.
Berechnen Sie die folgenden Wahrscheinlichkeiten oder geben Sie den R-Befehl zur Berechnung
dieser Wahrscheinlichkeiten an.
Hinweis: Falls Sie sich zweimal für den R-Befehl entscheiden, verwenden Sie mindestens einmal
den R-Befehl für die standardisierte Zufallsvariable!
P(X ≥ 505) =
P(496 ≤ X ≤ 502) =
[ 29 ] IV07S
Die Zufallsvariable X sei normalverteilt mit den Parametern µ = 50 und σ = 10.
Bestimmen Sie die folgende Wahrscheinlichkeit oder geben Sie den R-Befehl zur Berechnung dieser
Wahrscheinlichkeit mit Hilfe der standardisierten Zufallsvariablen an.
P(40 ≤ X ≤ 60) =
14
6 Stetige Verteilungen
15
[ 30 ] II07S1
Die folgende Abbildung zeigt die Dichtefunktion einer in der Vorlesung behandelten bekannten Verteilung.
Dichtefunktion
0.5
0.4
y
0.3
0.2
0.1
0.0
0
5
10
15
20
x
Bestimmen Sie den Parameter der Verteilung aus der Abbildung.
Parameter =
Berechnen Sie mit dem oben bestimmten Parameter der Verteilung die folgende Wahrscheinlichkeit
oder geben Sie den R-Befehl zur Berechnung dieser Wahrscheinlichkeit an.
Hinweis: Falls Sie nicht in der Lage sind, den Parameter zu bestimmen, dann (und nur dann) verwenden Sie bitte den nicht korrekten Wert 0.3 für den Parameter.
P(5 < X < 10) =
[ 31 ] IV07S1
Welche Ausgabe ergibt der R-Befehl qnorm(0.5, 100, sd = a)?
Hinweis: Die Ausgabe hängt nicht davon ab, welchen Wert für a man eingibt.
Ausgabe des R-Befehls:
6 Stetige Verteilungen
16
D: Lösungen
1) b, e
2) b, c, e
3) b, c
4) -2 ; 2
5) 0.841 ; 0.159 ; 0.159





6) 20 ; 0 ; 1 ; 15 ; 8.333 ; 0.5 ; 0.2 ; 0.4 ; 0.5 ; F(x) =
7) 1.2
8) b, d, e
9) a, c, d, e
10) 1.53
11) 0.841 ; 0.954 ; 0 ; 0.159
12) 0.682 ; 0.309 ; 0.382 ; 0.159
13) a, b, c, e
14) e(−1.6)
15) 12.5
16) 2.5
17) 6
18) 2 ; 1 ; 0.35 ; 0.632 ; 0.018
19) 0.191 ; pnorm(0,0,2)-pnorm(-1,0,2)
20) 0.08
21) 0.8869 ; 0.0821 ; 0.3297
22) 0.2209 ; 0.2444 ; 0.1524
23) b, c, d, e
24) a, b, c, d, e
25) 0.5




0
x < 10
x − 10
für 10 ≤ x ≤ 20
10
1
x > 20
6 Stetige Verteilungen
26) 0.632 ; sum(dbinom(46:54,100,0.5)) ; pbinom(54,100,0.5)-pbinom(45,100,0.5)
27) 16 ;
√
1
;4; 3
4
28) 0.047 ; 1-pnorm((505-500)/3,0,1) ; 0.657 ; pnorm(502,500,3)-pnorm(496,500,3)
29) 0.682
30) 0.25 ; 0.204
31) 50
17