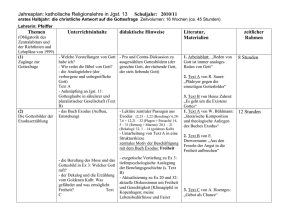
Michelson-Interferometer
Werbung

UE Physik und Biophysik G. Moser, M. Musso, K. Plätzer, R. Schwarzenbacher Michelson Interferometer Aufgabenstellung: Die Funktionsweise eines Michelson-Interferometers wird untersucht (Demo siehe http://www.activeart.de/dimshops/demo/interferometer ). Als Anwendung wird einerseits der Wellenlängenabstand der zwei gelben Natrium Spektrallinien D1 und D2, und andererseits die Brechzahl einer Glasplatte, unter Benutzung des Michelson Interferometers, bestimmt. Experimentelle Vorgangsweise: A) Das Michelson-Interferometer: Das hier verwendete Experimentier-MichelsonInterferometer besteht aus einem Strahlteiler, einem fixen und einem über Mikrometerschraube und Hebelmechanismus beweglichen Spiegel, alles montiert auf einer massiven Grundplatte. Als Lichtquelle dient entweder eine Natrium-Dampflampe (weitgehend monochromatisch, λmittel = 589.3 nm) oder eine Reuterlampe (Weißlichtquelle). Die Interferenzerscheinung ist verknüpft mit dem unterschiedlich langen Weg des Lichtes vom Strahlteiler zum beweglichen Spiegel (Strecke LSp1) und vom Strahlteiler zum fixen Spiegel (Strecke LSp2). Konstruktive Interferenz ergibt sich wenn der optische Gangunterschied 2 nLuft ΔL (wobei ΔL = LSp2 - LSp1 ) ein ganzzahliges Vielfaches m der Wellenlänge λmittel ist : Schematischer Aufbau des Michelson-Interferometers Jeder m ⋅ λ = 2 ⋅ n Luft ⋅ Δ L beobacht ete Interferenzstreifen entspricht also einen bestimmten optischen Gangunterschied 2 nLuft ΔL und ist charakterisiert durch die Ordnungsnummer m. B) Justieren des Interferometers: Zunächst soll das Interferometer auf optischem Gangunterschied Null eingestellt werden. Mit Hilfe der NatriumDampflampe soll durch vorsichtiges Drehen an den Justierschrauben des fixen Spiegels das Interferometer so justiert werden, daß ein konzentrisches Ringsystem von hellen und dunklen Interferenzstreifen zu sehen ist. Nun wird der bewegliche Spiegel über die Mikrometerschraube soweit verschoben, daß die Interferenzstreifen möglichst groß werden bzw. das Ringsystem nur mehr ganz wenige Ringe aufweist (optimal ein einzelner Ring). Dreht man weiter, dann sind wieder mehr Ringe zu sehen, man entfernt sich wieder von der Lage mit optischem Gangunterschied Null. Hat man das Interferometer optimal eingestellt, dann soll durch vorsichtiges Drehen an den Justierschrauben des fixen Spiegels die Interferenzstreifen vertikal gestellt werden. Dreht man mit der Mikrometerschraube in die eine oder andere Richtung, dann erkennt man, daß die Streifen sich zu krümmen beginnen. Sind die Streifen (mit Hilfe der Mikrometerschraube) wieder vertikal eingestellt, dann wird die Natrium-Dampflampe mit der Reuter-Lampe ersetzt und durch vorsichtiges Drehen an der Mikrometerschraube werden die sogenannten Weißlicht-Interferenzstreifen gesucht. Sind sie gefunden worden, werden sie mittig eingestellt und die Lage S0 des beweglichen Spiegels an der Mikrometerschraube abgelesen. C) Änderung des Gangunterschiedes: Die Reuterlampe wird durch die Natrium-Dampflampe ersetzt, vertikale gelbe und dunkle Interferenzstreifen sind zu sehen. Nun soll der bewegliche Spiegel so verschoben werden, indem die Mikrometerschraube sehr vorsichtig in einer Richtung gedreht wird, daß 200 Interferenzstreifen einzeln abgezählt werden können (Fadenkreuz im Strahlengang stellen). Die Endposition S200 der Schraube wird abgelesen. Die folgende Beziehung für die Änderung Δm der Interferenzordnung mit der Änderung Δx des mechanischen Gangunterschiedes (in diesem Fall Δx = LSp1,200 - LSp1,0 ) soll überprüft werden: Δm ⋅ λ mittel = 2 ⋅ n ⋅ Δx (2) (1) wobei n die Brechzahl der Luft bedeutet und hier gleich 1 gesetzt werden kann. Aufgrund des Hebelmechanismuses gilt: Δx = ΔS / 5 (3) wobei in diesem Fall ΔS = S200 - S0 ist. Sowohl aus der Beziehung (2) wie aus der Beziehung (3) soll Δx berechnet werden und miteinander verglichen werden. D) Wellenlängenunterschied der zwei gelben Spektrallinien der Natrium-Dampflampe: Das Interferometer wird wieder in Nullposition gebracht (Weißlicht-Interferenzstreifen sichtbar). Nun wird an der Mikrometerschraube soweit gedreht, bis die gelben und die dunklen Interferenzstreifen sich weitgehend vermischen und fast nicht mehr zu unterscheiden sind. Die Positition S1 der Mikrometerschraube wird notiert. Danach wird die Schraube weiter gedreht, bis die Interferenzstreifen wieder deutlich erscheinen und dann weiter bis sie wieder fast nicht mehr zu unterscheiden sind. Die Positition S2 der Mikrometerschraube wird notiert. Bei einem Michelson-Interferometer ist der kleinste auflösbare Wellenlängenunterschied Δλ zweier Spektrallinien mit den Wellenlängen λ und λ + Δλ gegeben durch Δλ = λ2 2 ⋅ Δx (4) Diese Beziehung erlaubt somit unmittelbar die Berechnung des Wellenlängenunterschiedes Δλ aus der Verschiebung Δx = (S2 - S1 ) / 5 des beweglichen Spiegels. Der so ermittelte Wert soll verglichen werden mit tabellierten Werten (siehe z.B. WALCHER). E) Brechzahl von Glas: Das Interferometer wird wieder in Nullposition gebracht (Weißlicht-Interferenzstreifen sichtbar). Die Positition S0 der Mikrometerschraube wird notiert. Nun wird vor dem beweglichen Spiegel eine Planplatte aus Glas in Form eines Objektträgers senkrecht zur optischen Achse positioniert. Die Weißlicht-Interferenzstreifen sind nicht mehr sichtbar. Die Mikrometerschraube wird vorsichtig in Uhrzeigersinn gedreht, bis die Weißlicht-Interferenzstreifen wieder erscheinen (etwas verformt). Die Positition S0,Glas der Mikrometerschraube wird notiert. Die Brechzahl nGlas der Glasplatte läßt sich aus der Beziehung: ⎛ Δx ⎞ nGlas = nLuft ⋅ ⎜ 1 + ⎟ d ⎠ ⎝ (5) wobei nLuft die Brechzal von Luft (in diesem Fall mit ausreichender Genauigkeit nLuft = 1), d die Dicke der Glasplatte und Δx = ( S0 - S0,Glas) / 5 ist. Der ermittelte Wert soll verglichen werden mit tabellierten Werten (siehe z.B. WALCHER). Vorbereitung: Trautwein, Kreibig, Oberhauser, Hüttermann: Physik für Mediziner, Biologen, Pharmazeuten, 5. Auflage 2000, Walter de Gruyter Kap. 18.1 Interferenz von Wellen; Kap. 18.1.1 Interferenzfähigkeit; Kap. 18.1.2 Anwendung der Interferenz: die Interferometrie; Kap. 18.1.3 Holographie. W. Hellenthal: Physik für Mediziner und Biologen, 7. Auflage 2002, Wissenschaftliche Verlagsgesellschaft mbH Stuttgart Kap. 8.3 Wellenoptik; Kap. 8.3.1 Kohärenz und Interferenz. V. Schünemann: Biophysik, 2005, Springer Kap. 4.7 Infrarot-(IR)-Spektroskopie: Absorption von elektromagnetischer Strahlung im Infrarotbereich macht Schwingungen innerhalb von Proteinen sichtbar; Kap. 4.7.1 Intramolekulare Schwingungen werden durch Lichtquanten im Infrarotgebiet angeregt; Kap 4.7.2 Anwendungen der IR-Spektroskopie in der Biologie. B. Nölting: Methods in Modern Biophysics, 2006, Springer Kap. 5.1 Spectrometers and devices; Kap. 5.1.2 Fourier transform infrared (FTIR) spectrometers; Kap. 5.2 Applications; Kap. 7.3 Scanning nearfield optical microscope (SNOM); Kap. 7.3.1 Overcoming the classical limits of optics. Schlagworte: * Interferometer, Zweistrahlinterferenz, Vielstrahlinterferenz * Zeitliche Kohärenz, räumliche Kohärenz * Weißlicht-Interferenz Web-Links • Michelson-Interferometer: Demo http://www.activeart.de/dim-shops/demo/interferometer • FT-IR-Spektroskopie: http://www.ir-spektroskopie.de/spec/ftir-prinzip/ • Interferenz: http://micro.magnet.fsu.edu/optics/lightandcolor/interference.html • Interferenz von zwei Wellen (Amplitude, Wellenlänge, Phase): http://micro.magnet.fsu.edu/primer/java/scienceopticsu/interference/waveinteractions/index.html • Interferenz von zwei Wellen: http://www.phy.ntnu.edu.tw/java/waveSuperposition/waveSuperposition.html • Anwendungsbeispiel Differential Interference Contrast (DIC) Mikroskopie: http://micro.magnet.fsu.edu/primer/virtual/dic/index.html