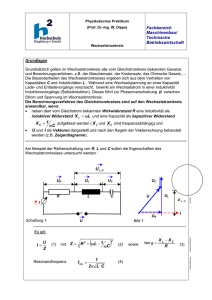
E 4 Spule und Kondensator im Wechselstromkreis

E 4 Spule und Kondensator im Wechselstromkreis
1.
Aufgaben
1.
Die Scheinwiderstände einer Spule und eines Kondensators sind in Abhängigkeit von der Frequenz zu bestimmen und gemeinsam in einem Diagramm
darzustellen.
2.
Aus der Frequenzabhängigkeit der Scheinwiderstände von Spule und Kondensator sind die Induktivität und der ohmsche Widerstand der Spule sowie
die Kapazität des Kondensators zu bestimmen.
3.
An einer Reihenschaltung aus Spule und Kondensator sind bei einer bestimmten Frequenz die Teilspannungen zu messen und das Zeigerdiagramm
darzustellen. Der Betrag der resultierenden Spannung ist anzugeben.
4.
Die Resonanzkurve I/U=f(f) des Reihenschwingkreises ist aufzunehmen und
grafisch darzustellen. Die Parameter Resonanzfrequenz f0, Resonanzmaximum (I/U)max und Bandbreite )f sind zu ermitteln und mit rechnerischen
Werten zu vergleichen.
2.
Grundlagen
2.1 Literatur:
[1] bis 10. Aufl.: E.5.0.1.; E.5.0.2.; E.5.0.4.;
ab 11. Aufl.: E.1.0.3 und Physik-Lehrbücher
2.2 Wechselspannung und Wechselstrom
Bei der Spannungserzeugung in Generatoren und bei der elektronischen
Schwingungserzeugung in Oszillatorschaltungen spielen sinusförmige Wechselspannungen und -ströme in der Technik und im Haushalt eine wichtige Rolle. Im
Wechselstromkreis sind die Spannung und die Stromstärke harmonische (d. h.
sinusförmige) Funktionen der Zeit:
(1)
1
E4
Wechselstromkreis
U0, I0 - Amplituden (Scheitelwerte) von Spannung und Strom, T = 2Bf - Kreisfrequenz (f - Frequenz), nU, nI - Nullphasenwinkel von Spannung und Strom.
Effektivwerte
Meist werden für Spannung und Stromstärke anstelle der Scheitelwerte die
Effektivwerte angegeben. Der Effektivwert Ieff ist der zeitlich quadratische Mittelwert eines Wechselstromes und entspricht derjenigen Gleichstromstärke, die an
einem Widerstand R den gleichen Leistungsumsatz P erzeugt. Für die an R in
Wärme umgesetzte momentane Leistung P(t) gilt für nU = nI = 0 (d. h. Spannung
und Stromstärke in Phase)
(2)
Der zeitliche Mittelwert von sin2(Tt) über eine Periodendauer T ist ½ und die über
eine Periodendauer gemittelte Leistung entsprechend
(3)
Der Vergleich mit
(4)
liefert für den Effektivwert der Stromstärke
(5)
analog gilt für den Effektivwert der Spannung
(6)
Die Netzspannung im Haushalt hat einen Effektivwert Ueff = 220 V und demnach
einen Scheitelwert von U0 = 311 V. Drehspul- und Digitalmessgeräte zeigen i.a.
Effektivwerte an.
2
Wechselstromkreis
E4
2.2.1 Spule und Kondensator im Wechselstromkreis
Befinden sich induktive und kapazitive Widerstände im Wechselstromkreis, treten
gegenüber ohmschen Widerständen folgende Besonderheiten auf:
a) Die Wechselstromwiderstände von Spule und Kondensator sind frequenzabhängig.
Der induktive Widerstand einer idealen Spule (ohmscher Widerstand R=0)
ist der (Kreis-)Frequenz des Wechselstromes direkt proportional, Proportionalitätskonstante ist die Induktivität L der Spule:
(7)
Diese Beziehung ist aus dem Induktionsgesetz ableitbar.
Der kapazitive Widerstand des idealen Kondensators mit der Kapazität C
ist dagegen der Kreisfrequenz umgekehrt proportional:
(8)
Diese Beziehung erhält man durch Differentiation der Definitionsgleichung
der Kapazität Q = C U.
b)
Spulen und Kondensatoren bewirken eine Phasenverschiebung zwischen
Spannung und Strom. Beim ohmschen Widerstand mit dem Wirkwiderstand
R sind Strom und Spannung in Phase und elektrische Energie wird in Wärme
umgesetzt. Ein rein induktiver Widerstand (ideale Spule) bewirkt, dass die
Spannung der Stromstärke um 90o vorauseilt, beim rein kapazitiven Widerstand (idealer Kondensator) eilt die Spannung der Stromstärke um 90o nach
(Abb. 1). Daraus folgt, daß an der (idealen) Spule und am (idealen) Kondensator im zeitlichen Mittel keine Leistung umgesetzt wird (Blindleistung,
Blindwiderstände). Sie stellen Speicher für magnetische oder elektrische
Energie dar.
Die Phasenverschiebung n (= nU - nI) zwischen Spannung und Stromstärke hat
zur Folge, dass Widerstände im Wechselstromkreis nicht einfach algebraisch
addiert werden können.
3
E4
Wechselstromkreis
Abb. 1:
Phasenverschiebung
zwischen Strom und Spannung im Wechselstromkreis
Effektiv ist die Behandlung von Wechselstromkreisen in komplexer Schreibweise
(Gaußsche Zahlenebene, Aufspaltung einer Größe in Real- und Imaginärteil), wie
auch in [1].
Die geometrische Entsprechung, das sogenannte Zeigerdiagramm, lässt sich
jedoch auch ohne Kenntnis der komplexen Zahlenrechnung darstellen und verstehen. Im Zeigerdiagramm werden Widerstände durch Zeiger dargestellt, deren
Längen den Beträgen proportional sind und deren Winkel zur Abszisse die durch
die Widerstände bewirkten Phasenverschiebungen zwischen Strom und Spannung
ausdrücken. Die Addition von Widerständen (in Reihenschaltungen) bzw. von
Leitwerten (in Parallelschaltungen) erfolgt analog zur Vektorrechnung.
Bei einer Reihenschaltung aus Spule, Kondensator und ohmschem Widerstand
(Abb. 2a) wird als Bezugsgröße der ohmsche Widerstand positiv an der Abszisse
aufgetragen, der Betrag des induktiven Widerstandes positiv an der Ordinate und
der des kapazitiven Widerstandes negativ an der Ordinate aufgetragen (Abb. 2b).
Der Gesamtwiderstand (Scheinwiderstand Z) ergibt sich durch geometrische
Addition zu
4
Wechselstromkreis
E4
Abb. 2a: Reihenschaltung von
R, L und C
Abb. 2b: Zeigerdiagramm
für Widerstände
(9)
Der Winkel n zwischen Zeiger von Z und Abszisse entspricht dem Phasenwinkel,
um den Strom und Spannung im Wechselstromkreis gegeneinander verschoben
sind. Nach Abb. 2b ergibt sich
(10)
Im Gegensatz zur idealen Spule (ohmscher Widerstand = 0) muss bei der realen
Spule neben dem induktiven Widerstand TL der ohmsche Widerstand RL der
Spulenwicklung als zur Induktivität in Reihe geschaltet berücksichtigt werden.
Der Scheinwiderstand Z der realen Spule ergibt sich nach (9) bzw. Abb. 2b zu
(11)
Bei der Reihenschaltung von R, L und C ist RL und R zu addieren.
5
E4
Wechselstromkreis
Beim realen Kondensator kann wegen nichtidealer Isolation ein Verlustwiderstand auftreten, der durch einen parallel zur Kapazität C geschalteten ohmschen
Widerstand RC berücksichtigt wird. In der Regel ist jedoch der Verlustwiderstand
RC so groß, dass er vernachlässigt werden kann und Gleichung (8) gilt.
Unter Berücksichtigung des besonderen Verhaltens von Wechselstromwiderständen ((a) und b) unter 2.2.1) gilt für den Wechselstromkreis ebenfalls das
Ohmsche Gesetz, es lautet bei Verwendung der Scheitelwerte von Strom und
Spannung
(12)
und gilt bei konstanter Frequenz und konstanter Temperatur. Anstelle der Scheitelwerte können auch die Effektivwerte (s. 2.2) eingesetzt werden.
Wechselspannungen und -ströme lassen sich ebenfalls in einem Zeigerdiagramm
darstellen, wie Abb. 3 für die Reihenschaltung von R, L und C zeigt. Auf der
Abszisse wird der durch alle drei Bauelemente in gleicher Stärke fließende Strom
I und der Spannungsabfall am ohmschen Widerstand UR aufgetragen. UL wird
positiv und UC negativ an der Ordinate aufgetragen. Durch vektorielle Addition
ergibt sich die Gesamtspannung U, die der an die Reihenschaltung angelegten
Spannung entspricht. Die algebraische Summe der Spannungsabfälle an R, L und
C kann dagegen erheblich größer als die angelegte Spannung sein.
Abb. 3:
Zeigerdiagramm für Spannungen
6
Wechselstromkreis
E4
2.3 Elektrische Schwingungen - Reihenschwingkreis
Die Reihenschaltung von Spule, Kondensator und ohmschem Widerstand stellt
einen elektrischen Schwingkreis dar (Abb. 2a). Schließt man diese Reihenschaltung bei aufgeladenem Kondensator kurz, so führt die Anordnung eine freie
gedämpfte elektrische Schwingung mit der Eigenkreisfrequenz T0 aus. Bei der
Entladung des Kondensators über die Spule wird in dieser eine Spannung induziert, die den Kondensator erneut (aber mit umgekehrter Polarität) auflädt. Die
elektrische Feldenergie des Kondensators und die magnetische Energie der Spule
wandeln sich periodisch ineinander um.
Wird dieser Schwingkreis an eine Wechselspannungsquelle der Spannung U
angeschlossen, so führt er erzwungene elektrische Schwingungen mit der Frequenz der Spannungsquelle aus. Die Stromstärke I ergibt sich nach (9) und (12)
zu
(13)
Nach (13) wird bei einer bestimmten Frequenz die Stromstärke maximal,
wenn TL - 1/TC = 0 ist, sich also induktiver und kapazitiver Widerstand kompensieren. Die Stromstärke wird dann nur durch den ohmschen Widerstand begrenzt.
Die Spannungen an Spule und Kondensator können weit über der angelegten
Spannung liegen, kompensieren sich aber wegen unterschiedlicher Vorzeichen.
Diesen Fall nennt man Resonanz und die zugehörige Kreisfrequenz - die Resonanzfrequenz - ist identisch mit der Eigenkreisfrequenz des Schwingkreises
(14)
Diese Beziehung nennt man Thomsonsche Schwingungsgleichung.
Die Frequenzabhängigkeit des Stromes I(f) (Abb. 4) zeigt ein charakteristisches
Verhalten mit einem ausgeprägten Maximum. Die Frequenzlage des Maximums
ist gemäß (14) durch die Werte von L und C festgelegt. Das drückt sich bei der
7
E4
Wechselstromkreis
erzwungenen Schwingung im Maximalstrom Imax = U/R und in der Bandbreite )f
("Abstimmschärfe")
(15)
der Stromresonanzkurve aus. Die Bandbreite )f ist das Frequenzintervall zwischen den beiden Stellen in der Resonanzkurve mit I = Imax/%2 = 0,707 Imax (Abb.
4). Die Dämpfung bestimmt auch die Resonanzüberhöhung r, das ist das Verhältnis der Spannung im Resonanzfall an der Induktivität UL0 bzw. am Kondensator
UC0 zur Spannung U der Wechselspannungsquelle:
(16 a)
Mit UL0 = Imax T0L bzw. UC0 = Imax/T0C und U = ImaxR folgt
(16 b)
Mechanische Schwingungsvorgänge zeigen analoge Erscheinungen wie Eigenschwingung, erzwungene Schwingung, Resonanz und Dämpfung.
Abb. 4:
Amplitudenresonanz
eines Reihenschwingkreises
8
Wechselstromkreis
3.
E4
Hinweise zur Versuchsdurchführung und -auswertung
zu Aufgabe 1:
Es ist die Schaltung nach Abb. 5 aufzubauen (Kontrolle durch den Betreuer). Die
Handhabung des Funktionsgenerators wird in der Platzanleitung erklärt.
Für die Spule sind Ueff und Ieff sind im Frequenzbereich 20...200 Hz in Schritten
von 10 Hz zu messen und daraus der Scheinwiderstand Z zu berechnen. Anschließend ist die Messung analog mit dem Kondensator C durchzuführen.
Abb. 5:
Schaltung zu Aufgabe 1
ZL und ZC sind in Abhängigkeit von der Frequenz f in einem Diagramm darzustellen.
zu Aufgabe 2:
Zur Ermittlung der Induktivität L der Spule trägt man (ausgehend von Gleichung
(11)) ZL2 über T2 auf. Aus dem Anstieg der erhaltenen Geraden lässt sich die
Induktivität L und aus dem Absolutglied der ohmsche Widerstand der Spule RL
berechnen. RL wird zum Vergleich mit einem Multimeter direkt bestimmt.
Zur Bestimmung der Kapazität C des Kondensators trägt man gemäß Gleichung
(8) 1/Z über T auf und kann aus dem Anstieg der Geraden die Kapazität C ermitteln.
9
E4
Wechselstromkreis
zu Aufgabe 3:
Es ist die Schaltung nach Abb. 6 aufzubauen (Kontrolle).
Abb. 6:
Schaltung zu Aufgabe 3
Bei einer bestimmten Frequenz (s. Platzanleitung) sind die Spannungen an der
Spule USp und am Kondensator UC zu messen. USp setzt sich gemäß Abb. 6 aus UL
und URL (Spannung an Induktivität bzw. ohmschem Widerstand der Spule) zusammen. Zunächst sind UL und URL mit Hilfe der folgenden Beziehungen aus den
Größen USp, L und RL zu berechnen:
Der Betrag der Spannung U ist zu errechnen und mit der gemessenen Eingangsspannung zu vergleichen.
Das Zeigerdiagramm für die Spannungen ist zu zeichnen. Die Teilspannungen
sind anzugeben.
zu Aufgabe 4:
Der Schwingkreis ist nach Abb. 7 mit C 1 aufzubauen (wegen des hohen ohmschen Widerstandes der Spule ist kein zusätzlicher ohmscher Dämpfungswiderstand notwendig). Für verschiedene Frequenzwerte ist die Spannung U und der
10
Wechselstromkreis
E4
Strom I zu messen und der Quotient I/U zu bilden. Die Schrittweite für f wird in
der Platzanleitung angegeben. Es ist eine grafische Darstellung I/U=f(f) anzufertigen (der I/U(f)-Verlauf gleicht dem I(f)-Verlauf. I/U(f) ist darzustellen,
weil die Ausgangsspannung des Funktionsgensgenerators etwas last- und frequenzabhängig ist.) und daraus die Resonanzfrequenz f0, Maximalstrom (I/U)max
und Bandbreite )f zu ermitteln. Diese Werte sind mit den nach (14) und (15)
berechneten zu vergleichen.
Abb. 7:
Reihenschwingkreis
4.
Schwerpunkte für die Versuchsvorbereitung
-
Amplitude, Effektivwerte von Wechselstrom und -spannung, induktiver und
kapazitiver Widerstand, Phasenverschiebung, Resonanzfrequenz, Scheinwiderstand, Blindwiderstand, Wirkwiderstand, Zeigerdiagramm
Ohmsches Gesetz für Wechselstrom, Induktionsgesetz, Definitionsgleichung
der Kapazität, Thomsonsche Schwingungsgleichung
-
11