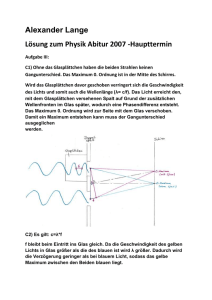
Elektronenbeugung

Teil 1:
Elektronenbeugung
1. Theorie
In den ersten beiden Jahrzehnten des zwanzigsten Jahrhunderts wurde klar, dass
das klassische Bild von Teilchen als kleine elastische Kugeln nicht für die Beschreibung der Physik der Atome ausreichend ist. So konnte im klassischen Bild die Existenz diskreter Spektrallinien bei der Lichtemission von Atomen nicht befriedigend erklärt werden. In Analogie zu den Teilcheneigenschaften des Lichts postulierte DE
BROGLIE 1923, dass Materieteilchen wie Elektronen sich wie Wellen mit der Wellenlänge

h
h

p mv
(1)
(h : PLANCKsches Wirkungsquantum, p : Impuls, m : Masse und v : Geschwindigkeit
des Teilchens)
verhalten.
DAVISSON und GERMER zeigten 1927, dass man mit Elektronen die gleichen Beugungsbilder an Kristallen erzeugen kann wie mit Röntgenstrahlen. THOMPSON erhielt
analog zur DEBYE-SCHERRER-Methode ähnliche Beugungsbilder an Kristallpulver.
In dem nun durchzuführenden Versuch wird die Beugung an einer polykristallinen
Graphitfolie untersucht, die wie Kristallpulver ebenfalls aus einer großen Anzahl zufällig orientierter Mikrokristalle besteht.
Bei der Elektronenbeugung am Kristallgitter gilt wie bei der Röntgenbeugung die
BRAGGsche Bedingung (s. a. Abb. 1):
2d sin   n
(2)
(d : Netzebenenabstand, : Reflexionswinkel, n : zugehörige Beugungsordnung)
Abb. 1: Geometrie der Beugung von Elektronen an einem Kristall.
Fallen nun Elektronenstrahlen auf die Graphitfolie, so sind aufgrund der willkürlichen
Anordnung der Mikrokristalle immer solche zu finden, die Glg. (2) erfüllen. Alle von
diesen Kristalliten ausgehenden gebeugten Strahlen liegen auf Kegelmänteln, deren
1
gemeinsame Achse durch die Einfallsrichtung der Elektronen gegeben ist. Die im
Versuchsaufbau realisierte Beugungsgeometrie ist schematisch in Abb. 2 für eine
Reflexion an einem ausgewählten Kristallit dargestellt.
Abb. 2: Schematische Darstellung der Versuchsanordnung.
Wie man sieht, stellt der Leuchtschirm der Röhre einen Schnitt durch die erwähnten
Kegel dar, so dass die gebeugten Elektronenstrahlen als konzentrische Kreise um
den ungebeugten Elektronenstrahl erscheinen.
Aus Abb. 2 lässt sich folgende Beziehung ableiten:
tan  2i  
Ri
L
(3)
(Ri : Durchmesser des Kreises auf dem Leuchtschirm,
L : Abstand zwischen Leuchtschirm und Probe)
B
B
Der Index i bezeichnet den betrachteten Reflex. Da für kleine Winkel näherungsweise
tan  2   sin  2   2sin 
(4)
gilt, folgt mit Glg. (2) für die hier betrachtete erste Beugungsordnung
Ri 
L
 .
di
(5)
2. Versuchsaufbau und -durchführung
Abb. 3 zeigt eine Skizze des verwendeten Versuchsaufbaus. Er besteht im Wesentlichen aus einer evakuierten Elektronenröhre, die mit einem Fluoreszenzschirm zur
Visualisierung der Elektronen ausgestattet ist. Die aus der Glühkathode austretenden
Elektronen werden durch eine Anode beschleunigt. Zur optimalen Fokussierung des
Elektronenstrahls werden jeweils zwei Kathoden und Anoden verwendet. Die Elek-
2
tronen werden an der in der zweiten Anode integrierten Graphitfolie gebeugt und
gelangen schließlich auf den Schirm.
Zu Beginn des Experiments werden die Spannungen an den beiden Netzteilen wie
folgt eingestellt:
WEHNELT-Zylinder (G1): -25 V,
Vorbeschleunigungsspannung (G2): + 300 V (als Fixspannung am Netzteil),
Anodenhochspannung (G3): bis + 10 kV (variabel),
Fokussierspannung (G4): + 250 V,
Heizspannung: 6,3 V.
B
B
B
B
B
B
B
B
Abb. 3: Skizze des Versuchsaufbaus.
Für die kinetische Energie Ekin der Elektronen gilt:
B
B
Ekin 
1
m  v2  e U
2
(6)
(e : Elementarladung, U : Spannung)
Damit ergibt sich für die DE BROGLIE-Wellenlänge mit Glg. 1:

h
2emU
3
(7)
Abb. 4: Aufbau des Kristallgitters von Graphit.
Auf dem Fluoreszenzschirm bilden sich Interferenzringe aus, aus deren Radien Ri
sich mit Hilfe von Glg. (5) und (7) die beiden Gitterkonstanten d1 und d2 (s. Abb. 4)
bestimmen lassen.
B
B
B
B
B
B
3. Aufgabenstellung
Messen Sie die zu den Gitterkonstanten d1 und d2 gehörigen Radien R1 und R2
auf dem Fluoreszenzschirm für verschiedene (mindestens fünf) Beschleunigungsspannungen U (G3) aus.
B
B
B
B
B
B
B
B
B
B
4. Auswertung
Berechnen Sie jeweils  nach Glg. (7) und tragen Sie Ri gegen  auf. Bestimmen
Sie aus den Steigungen der Geraden die Gitterkonstanten d1 und d2. Der Abstand
L zwischen Präparat und Leuchtschirm beträgt 127 ± 3 mm.
B
B
B
4
B
B
B
Teil 2:
Der lichtelektrischer Effekt
5. Einleitung - Historische Bedeutung
Ende des 19. Jahrhunderts galt die Physik als nahezu vollständig. Fast alle beobachteten physikalischen Effekte waren im Rahmen der klassischen Physik verstanden und nur wenige Beobachtungen konnten noch nicht erklärt werden. Physik hatte
damals den Ruf wenig zukunftsträchtig zu sein. Doch wie so häufig war auch diese
Zukunftsprognose falsch, denn die wenigen noch nicht verstandenen Phänomene
sollten den Weg zu einer Revolution in unserem Verständnis der Natur führen und
der Quantenmechanik der Weg ebnen.
Eine der nicht verstandenen Beobachtungen betraf die Licht-Materie Wechselwirkung. Klassisch erwartete man folgendes:
Durch das elektrische Wechselfeld des Lichtes (elektromagnetische Welle) werden
die Elektronen im Atom zu (erzwungenen) Schwingungen wachsender Amplitude
angeregt. Nach einiger Zeit haben sie ausreichende Energie, das Atom zu verlassen. Bei geringer Lichtintensität (die Amplitude der elektrischen Feldstärke ist klein)
ist der Energieübertrag an die Elektronen kleiner. Sie haben also nach Überwindung
der Ablösearbeit eine geringere kinetische Energie.
Bei niedrigerer Frequenz des Lichtes schwingen die Elektronen langsamer. Je nachdem, ob mit der Frequenz des Lichtes eine Resonanzstelle für Elektronenschwingungen getroffen ist, geschieht die Energieübertragung mehr oder weniger gut. Je
weiter weg sich die Erregerfrequenz von der Resonanzfrequenz befindet, umso länger dauert es, bis die nötige Energie aufgenommen ist. Alle Elektronen nehmen
gleichmäßig aus dem Feld Energie auf, erreichen also auch alle zugleich die zur Ablösung nötige Energie, werden also nach Ablauf der Energieaufnahmezeit alle auf
einmal ausgelöst.
Bestrahlt man also eine Photokathode mit Licht, so sollte die kinetische Energie der
austretenden Elektronen von der Intensität (Amplitude) des bestrahlenden Lichts abhängen. Die benutzte Lichtwellenlänge (Lichtfrequenz) sollte dabei keine Rolle spielen. Es würde lediglich erwartet werden, dass es bei niedriger Wellenlänge länger
dauert, bis die ersten Elektronen die Photoelektrode verlassen. Die tatsächlichen
Beobachtungen waren jedoch gänzlich andere. Man fand, dass:




die kinetische Energie der Elektronen linear mit der Frequenz des bestrahlenden Lichts anwächst. (Resonanzen werden nicht beobachtet!),
es eine maximale Wellenlänge des Lichtes gibt, oberhalb derer keine Elektronen mehr emittiert werden,
die Maximalwellenlänge vom Material der Photokathode abhängt und
die Freisetzung der Elektronen bereits wenige Nanosekunden nach der Bestrahlung beginnt und genauso schnell nach dem Abschalten des Lichts wieder aufhört.
5
Im Jahre 1905 gelang Albert EINSTEIN dann mit Hilfe des PLANCKschen Strahlungsgesetzes die Erklärung dieses Effekts. Für diese Arbeit (nicht für die bis dahin sehr
umstrittene Relativitätstheorie) bekam er 1921 den Nobelpreis. Bis heute gilt der
lichtelektrische Effekt als eines der Schlüsselexperimente zur Entwicklung der
Quantenmechanik.
6. Theorie
Albert EINSTEIN nahm an, dass das Licht aus einem Strom von Teilchen (Photonen)
besteht, eine Annahme, die im krassen Gegensatz zur bisherigen Betrachtungsweise
des Lichts als Welle stand. Die Energie der Teilchen setzte er mit E  h an, wobei
  c  , die Frequenz der bestrahlenden Lichts ist. Die Lichtgeschwindigkeit ist c und
die Wellenlänge des Lichts ist 
Die kinetische Energie Ekin der herausgeschlagenen Elektronen ergibt sich dann aus
der Photonenenergie minus der Austrittsarbeit WA

h
h

p mv
(8)
Ist die Photonenenergie kleiner als die Austrittsarbeit, so erhält man negative Werte
für die kinetische Elektronenenergie. In diesem Fall werden keine Elektronen emittiert. Die Schwellfrequenz, ab der Elektronen emittiert werden, beträgt also:
WA

h
(9)
Gleichung (8) zeigt, dass die kinetische Energie linear mit der Lichtfrequenz ansteigt.
Da das Licht wie ein Teilchen betrachtet wird, kann man das Auftreffen der Lichtquanten auf die Anode als einen Stoß betrachten, bei dem die Energie der Lichtteilchen auf die Elektronen übertragen wird. Daher werden die Elektronen innerhalb weniger Nanosekunden freigesetzt. Die Austrittsarbeit ist eine Materialkonstante. Beispielwerte finden sich in Tabelle 1:
Tabelle 1: Elektronen-Austrittsarbeit für
einige Elemente
Element
Austrittsarbeit WA in
eV
Li
Na
K
Rb
Cs
Cu
Ag
Au
Ni
Pt
2,93
2,36
2,29
2,26
1,95
4,53
4,63
5,38
5,53
5,64
6
7. Versuchsaufbau und -durchführung
Der Versuchsaufbau ist in Abb. 5 dargestellt. Eine vereinfachte schematische Darstellung des Aufbaus ist in Abb. 6 gegeben.
Abb. 5: Versuchsaufbau.
Abb. 6: Schematische Darstellung der Versuchsanordnung.
Mit Hilfe einer Quecksilberdampflampe wird Licht erzeugt. Das von dieser Quecksilberdampflampe emittierte Licht basiert auf einer elektrischen Entladung von verdünntem Quecksilbergas. Dabei werden verschiedene elektronische Zustände des
Quecksilbers durch Stöße im Entladungskanal angeregt. Durch spontane Emission
fallen die Elektronen in niedrigere Energiezustände und schließlich in den Grundzustand. Dabei senden sie Licht aus, dessen Wellenlänge charakteristisch für die
Energiedifferenzen der einzelnen Zustände ist. Die Quecksilberdampflampe emittiert
daher ein ganzes Spektrum verschiedener Wellenlängen (s. Tabelle 2).
7
Tabelle 2: Wichtige
Emissionswellenlängen einer
Quecksilberdampflampe/nm
579,1
577,0
546,1
491,6
435,8
407,8
404,7
365,0
334,2
312,6
Mit Hilfe von Frequenzfiltern wird nun dafür gesorgt, dass nur eine ausgewählte
Wellenlänge in die Photozelle fällt. Eine Blende sorgt dafür, dass das Licht auf die
Kathode K und nicht auf die ringförmige Anode der Photozelle trifft.
Solange noch kein Licht auf die Elektrode K trifft, sind die Elektroden K und A elektrisch neutral, die Spannung zwischen diesen beiden Elektroden ist Null. Beim Auftreffen des Lichts lösen sich die ersten Elektronen aus Elektrode K. Abhängig von
der Photonenenergie und der Ablösearbeit des Elektrodenmaterials besitzen sie eine
bestimmte Anfangsgeschwindigkeit und damit kinetische Energie. Die ersten Elektronen werden von der Elektrode A kaum abgestoßen, da diese noch fast neutral ist.
Die nachfolgenden Elektronen (mit gleicher kinetischer Anfangsenergie wie die ersten Elektronen) werden von der nun zunehmend negativen Elektrode A abgestoßen,
sie erreichen diese aber noch. Aufgrund der Ladungstrennung (die Elektrode K wird
immer stärker positiv, Elektrode A wird immer stärker negativ) wächst die Spannung
zwischen beiden Elektroden. Schließlich ist die Abstoßung der später ausgelösten
Elektronen durch Elektrode A so stark, dass diese Elektronen nicht mehr dorthin gelangen können. Die Ladungstrennung hat eine Sättigung und damit die Spannung einen stabilen Endwert erreicht, der ein Maß für die kinetische Energie der Elektronen
ist. Es gilt:
U
Ekin
e
(10)
Diese Spannung wird mit einem hochohmigen Voltmeter gemessen. Abhängig von
der Frequenz der eingestrahlten Lichts werden sich verschiedene Spannungen einstellen.
8. Aufgabenstellung
Messen Sie die Photospannung für die fünf unterschiedlichen Lichtwellenlängen.
8
9. Auswertung
1. Bestimmen sie aus den gemessenen Photospannungen die kinetische Energie der Elektronen.
2. Tragen Sie anschließend die kinetische Energie gegen die Lichtfrequenz auf.
3. Bestimmen Sie aus dieser Auftragung die Austrittsarbeit des Kathodenmaterials. Um welches Material handelt es sich?
4. Bestimmen Sie aus der Steigung der Auftragung das PLANCKsche Wirkungsquantum.
5. Vergleichen Sie die erhaltenen Werte mit den Literaturdaten und diskutieren
Sie mögliche Messfehler.
10.
Literatur
1. H. R. HERTZ, Ueber einen Einfluss des ultravioletten Lichtes auf die electrische
Entladung, Annalen der Physik und Chemie 31, 983 (1887).
2. W. HALLWACHS, Ueber den Einfluss des Lichtes auf electrostatisch geladene
Körper, Annalen der Physik und Chemie 33, 301 (1888).
3. A. EINSTEIN, Über einen die Erzeugung und Verwandlung des Lichtes
betreffenden heuristischen Gesichtspunkt, Ann. Phys. 17, 132 (1905).
9