absatz preis Uv = + ⋅ +
Werbung

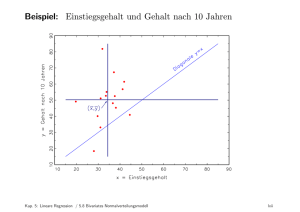
Um ein einfaches lineare Regressionsmodell aufzustellen, stehen uns folgende Variablen zur Verfügung: • • • Land, Absatz, Preis. Dia Variable „Land“ interessiert uns nicht so sehr, da wir uns im Endeffekt nur für den Absatz im gesamten Bundesgebiet interessieren. Wir unterstellen eine lineare Abhängigkeit des Absatzes vom Preis. Vermutlich werden wir bei einem geringen Preis viele Produkteinheiten verkaufen, während unser Absatz bei einem hohen Preis eher gering sein wird. Der Absatz variiert mit den verschiedenen Preisen und wird als zufällige Größe angesetzt. Das Regressionsmodell lautet dann folgendermaßen: absatzv = α + β ⋅ preisv + U v Wir gehen davon aus, dass ein mittlerer Absatz existiert, der manchmal über- und manchmal unterschritten wird. Es gibt einen „Grundabsatz“ α , der bei einem Preis von null abgesetzt würde. Dieser „Grundabsatz“ ist in diesem Fall nur eine theoretische Größe, die praktisch keine Bedeutung haben wird. Zu dem hypothetischen „Grundabsatz“ addieren wir den preisbedingten Absatz (bzw. wir subtrahieren, wenn er negativ ist). Im Gegensatz zur empirischen Regression berücksichtigen wir hier auch die Residuen U v . Diese Fehler sind unabhängige Zufallsvariablen und entsprechen an unterschiedlichen Stellen beobachteten Replikaten des allgemeinen Fehlers. Wir unterstellen, dass die Residuen bei null zentriert sind und die gleiche Varianz haben. Ferner sollen die Fehler voneinander unabhängig sein. Damit ist unser einfaches lineares Regressionsmodell zunächst vollständig beschrieben. Nun kann es mit der Schätzung der Koeffizienten weitergehen!