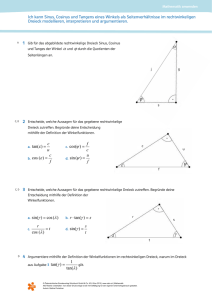
6) = 30°

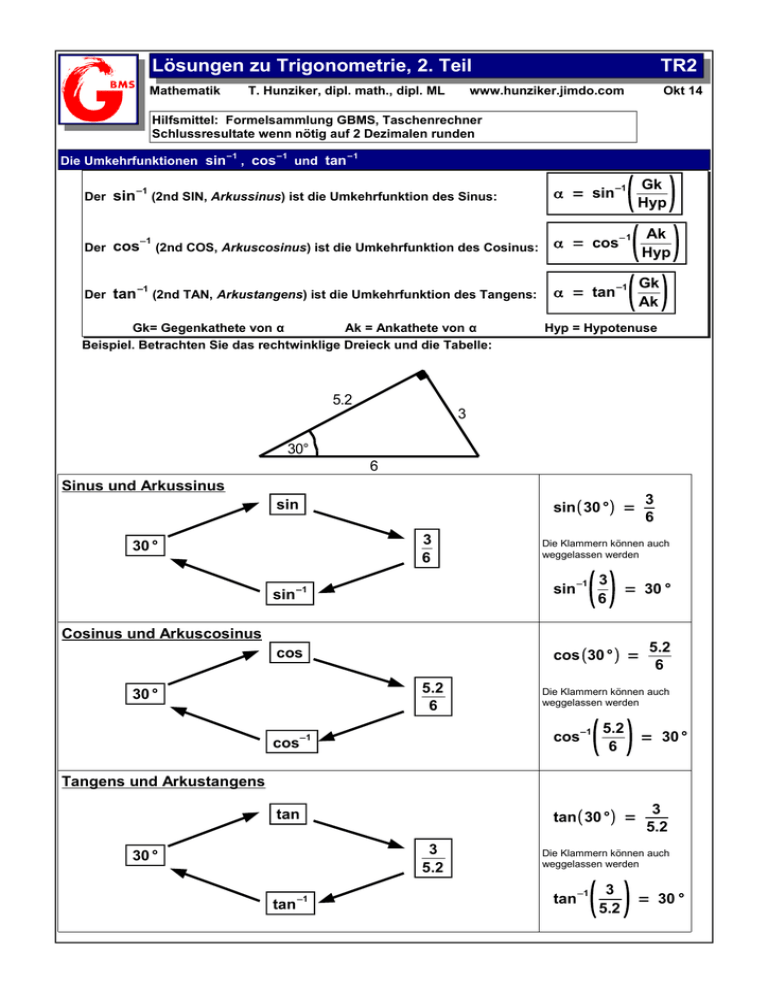
Lösungen zu Trigonometrie, 2. Teil
TR2
Mathematik
Okt 14
T. Hunziker, dipl. math., dipl. ML
www.hunziker.jimdo.com
Hilfsmittel: Formelsammlung GBMS, Taschenrechner
Schlussresultate wenn nötig auf 2 Dezimalen runden
−1
Die Umkehrfunktionen sin
−1
, cos
und tan
−1
α = sin−1
( )
( )
( )
Gk
Hyp
Der
sin−1 (2nd SIN, Arkussinus) ist die Umkehrfunktion des Sinus:
Der
Ak
−1
cos−1 (2nd COS, Arkuscosinus) ist die Umkehrfunktion des Cosinus: α = cos Hyp
Der
tan−1 (2nd TAN, Arkustangens) ist die Umkehrfunktion des Tangens:
Gk= Gegenkathete von α
Ak = Ankathete von α
Beispiel. Betrachten Sie das rechtwinklige Dreieck und die Tabelle:
5.2
α = tan−1
Gk
Ak
Hyp = Hypotenuse
3
30°
6
Sinus und Arkussinus
sin
3
6
sin( 30° ) =
3
6
30°
Die Klammern können auch
weggelassen werden
()
3
6
sin
sin−1
cos
cos(30° ) =
−1
= 30 °
Cosinus und Arkuscosinus
5.2
6
30°
Die Klammern können auch
weggelassen werden
( )
5.2
6
cos
cos−1
tan
tan( 30° ) =
−1
5.2
6
= 30°
Tangens und Arkustangens
3
5.2
30°
−1
tan
3
5.2
Die Klammern können auch
weggelassen werden
tan−1
( )
3
5.2
= 30 °
Runden Sie Schlussresultate auf 2 Dezimalen.
Aufgabe 1
Eine Leiter der Länge 7.5 m lehnt in der Höhe 6.6 m an einer senkrechten Wand.
Bestimmen Sie ihren Neigungswinkel α.
( )=
sin α = 6.6
7.5
→ α = sin−1 6.6
7.5
61.64 ° = α
7.5
6.6
a
Aufgabe 2
Berechnen Sie die fehlenden Seiten und Winkel der rechtwinkligen Dreiecke ABC (90°-Winkel bei C):
a
a) a = 6 cm, b = 2.5 cm
c
c = √ 62 + 2.5 2
c = 6.5 cm
( )
β = tan−1
2.5
6
b
B
A
b=2.5
C
a=6
C
b) b = 39.3 cm, c = 65.5 cm
a = √ 65.52 −39.3 2
a = 52.4 cm
α = cos−1
= 22.62 °
α = 90 ° − β = 67.38 °
( )
39.3
65.5
a
A
b
a
c=65.5
= 53.13 °
β = 90 ° − α = 36.87 °
Aufgabe 3
Das Dreieck ABC ist gleichschenklig (a=b). Berechnen Sie alle fehlenden Seiten und Winkel, sowie
den Flächeninhalt des Dreiecks.
α = sin−1
c
= x = √ 13 2−12 2 = 5 cm
2
→ c = 10 cm
β =
c⋅h
=
2
=
C
67.38 °

( =α)
b
γ = 180° – α – β
Flächeninhalt:
F =
( )
12
13
67.38 °
a = 13 cm, h = 12 cm
γ = 45.24°

A
2
60 cm
h =12
c
x
a=13

B
Aufgabe 4
Welche Steigung in Grad (auf 2 Dezimalen genau) hat eine Strasse mit einer Steigung von
a) 5%
−1
tan
( )
5
100
d) 200%
63.43°
b) 10%
=
c) 100%
5.71°
2.86 °
45°
Skizze:
e) p%
α = tan−1
( )
p
100
p
α
100
B
Aufgabe 5
Von folgendem Drachenviereck soll der Flächeninhalt berechnet werden:
D
sin 56 ° =
3.7
c
m
5.8
A 56°
cm
y
x
z
3.7
Flächeninhalt:
x = √ 3.72 −z 2 = 2.069cm
AC⋅BD
2
( x+ y)⋅2z
F=
2
y = √5.8 2 −z 2 = 4.922cm
F=
F=
z = (sin 56°)∙3.7 = 3.067 cm
C
z
7
3.
B
6.99⋅6.13
2
F = 21.45 cm2
Aufgabe 6
Ein Turmdach hat die Form einer regelmässigen quadratischen
Pyramide mit der Grundkante a = 4.28 m und der Höhe h = 6.45 m.
Bestimmen Sie den Neigungswinkel β einer Dachfläche, sowie
die Länge s und den Neigungswinkel α einer Seitenkante.
x=
a
= 2.14 m
2
tan β =
6.45
2.14
β = tan−1
y = PQ : 2 = 3.026 m
s = √ y +h
2
s
2
h
s = √ 3.026 2 +6.45 2
( )
6.45
= 71.65 °
2.14

s = 7.12 m
PQ = Diagonale des
Quadratss
PQ = √ 4.28 2 + 4.282 = 6.053 m
P
α = tan−1
(
6.45
3.026

x
y
Q
a
a = 4.28 m
)
α = 64.86 °
Aufgabe 7
a) Berechnen Sie den Winkel, den die
Raumdiagonale eines Würfels
mit einer Würfelkante bildet.
b) Berechnen Sie den spitzen Winkel, unter dem sich
zwei Raumdiagonalen eines Würfels schneiden.
B
Wähle Würfelkante = 1
Dann gilt:
α
AB = √ 12 + 12 +12
M
1
β
√2
AB = √3 ≈ 1.732
AM =
0.5
α
1
Wähle z.B. Kantenlänge = 1.
Dann gilt:
(√ )
α = tan−1
2
= 54.74 °
1
sin β =
A
Gk
0.5
=
Hyp 0.866
β = sin−1
(
0.5
0.866
)
= 35.26 °
α = 2⋅β = 70.53 °
√ 3 ≈ 0.866
2
Aufgabe 8
Zürich hat eine geographische Breite von 47.3°. Erdradius = 6370 km.
a) Welchen Umfang hat der Breitenkreis, auf dem Zürich liegt?
Resultat auf km runden.
Zürich
Breitenkreis
x
6370
x = ( cos 47.3 ° )⋅6370 = 4319.88 km
cos 47.3 ° =
47.3°
Umfang: u = 2 r π = 2 x π
u = 2⋅4319.88⋅π =
27'143 km
Ansicht von der Seite:
b) Mit welcher Geschwindigkeit v bewegt sich Zürich infolge der
Erddrehung auf dem Breitenkreis (siehe Abbildung rechts)?
Resultat auf ganze km/h runden.
Zürich
s
Weg
=
t
Zeit
Geschwindigkeit: v =
v
=
63
7
0
x
47.3°
x
27'143 km
km
= 1131
24 h
h
Aufgabe 9
Gegeben: ein regelmässiges 10-Eck mit der Seitenlänge s
Gesucht: der Flächeninhalt A des 10-Ecks, in Abhängigkeit von s
C
h
36°
A
tan 18° =
s
2
h
h⋅tan18 ° =
h =
s
2
18°
|: tan 18°
A ABC =
B
2
AABC =
s
4⋅tan18 °
Flächeninhalt des 10-Ecks:
Flächeninhalt des Dreiecks ABC:
s
⋅h
2
2
|⋅h
s
2⋅tan18 °
A ABC =
s
s2
10 s2
A 10 = 10⋅A ABC = 10⋅
=
4⋅tan 18 °
4⋅tan 18 °
| h einsetzen
s
s
⋅
2 2⋅tan18 °
A 10 =
5⋅s2
2⋅tan18 °
oder
A 10 = 7.694 s
oder
2
A10 =
2.5 s2
tan 18°