Das Modell der monopolistischen Konkurrenz
Werbung

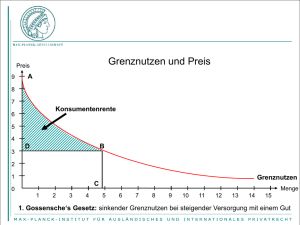
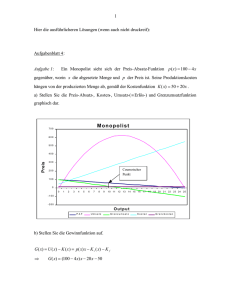
© Prof. Dr. C.C. von Weizsäcker 1 Das Modell der monopolistischen Konkurrenz © Prof. Dr. C.C. von Weizsäcker Der Anbieter sucht sich nun den optimalen, d.h. gewinnmaximierenden Preis. Er tut dies genau wie der Monopolist. Die bekannte Ableitung geht wie folgt, wobei G i den Gewinn bezeichnet: Gi = Umsatz − Kosten Die Wirtschaftstheorie verfügt über ein relativ einfaches Modell des Wettbewerbs mit heterogenen Gütern. Da die meisten Märkte solche mit heterogenen Gütern sind, ist dieses Modell für die Realität von größere r Relevanz als das Modell der vollkommenen Konkurrenz. Das Modell wurde das erste Mal entwickelt von Edward Chamberlin. Er gab der Marktform des heterogenen Polypols auch den Namen „monopolistische Konkurrenz“. Wir entwickeln das Modell unter Verwendung einiger vereinfachender Annahmen. = p ix i − k i ( Ableitung und Nullsetzung: dG dx (4) pi = ai − b i xi ) = a − bx x −f − g x i i i i i i i Es gibt eine große Anzahl von Anbietern, z.B. Friseurläden in einer Stadt, die zueinander in Konkurrenz stehen. Im ersten Schritt unterstellen wir die Anzahl der Anbieter, n, als fix. Später betrachten wir Marktzutritt und Marktaustritt. Wir betrachten einen beliebig herausgegriffenen Anbieter i. Dieser verlangt den Preis pi von seinem Kunden für eine Einheit seines Produkts. Er sieht sich konfrontiert mit einer PreisAbsatz-Funktion, die wir schreiben können (1) 2 i = a − 2b x − g = 0 i i i i i a − gi xi = i 2b i , woraus für den gewinnmaximierenden Preis p*i folgt: xi wobei die abgesetzte Menge ist. Die Bestimmungsfaktoren für die von dem Anbieter i nicht beeinflußbaren Werte ai und bi werden wir später diskutieren. (5) Anbieter i habe folgende Kostenfunktion a − g i ai + g i p* = a − b i = i i i 2b 2 i pi (2) Ki = f i + g ix i ai Die Kosten hängen also linear von der Produktionsmenge ab (= konstante Grenzkosten Gk i = gi ). Die Fixkosten fi > 0 führen dazu, daß der Anbieter mit der Ausbringung fallende Durchschnittskosten beobachtet. Das ist, wie der erfahrene Geschäftsmann weiß, in der Wirklichkeit fast immer der Fall. Die Durchschnitts -kosten d i sind ja Cournot-Punkt p*i (3) di = f +g x f i = i i i = i +g i x x i i i K x gi und damit offensichtlich mit steigendem xi fallend. xi* xi © Prof. Dr. C.C. von Weizsäcker 3 Der gewinnmaximierende Preis ist das arithmetische Mittel aus ai und gi , d.h. liegt auf der Mitte zwischen ai und gi . Nun kommt der Konkurrenzaspekt des Modells ins Spiel. Der Absatz von Anbieter i geht mit steigendem Preis pi vor allem deshalb zurück, weil die Kunden zu Konkurrenten abwandern. Wir erklären den Absatz eines Anbieters also aus der Preisdifferenz zwischen diesem Anbieter und anderen Anbietern. Am einfachsten machen wir das in der Form, daß wir den Abstand des Preises pi vom Durchschnittspreis p aller Anbieter zur erklärenden Größe für den Absatz xi machen. Damit wäre die Preisabsatzfunktion zu schreiben: (6) Wir betrachten nun die Bildung des Durchschnittspreises p auf dem gesamten Markt. Wir bezeichnen mit p$ den Durchschnitt der gewinnmaximierenden Preise p1*, p2*, p3*,..., pn*, also p* + p*2 +K+ p*n p$ = 1 n Gemäß der Formel (9) für den gewinnmaximierenden Preis pi *, i = 1, 2, ..., n, ergibt sich: pi = p + h i − b ix i p$ = p + h1 + g1 + p + h 2 + g2 +K+p + h n + g n 2n Wir haben den bisherigen Wert ai somit erklärt durch (8) a i = p + hi Dabei kann hi interpretiert werden als Produktdifferenzierungsvorteil des Anbieters i. Dieser Produktdifferenzierungsvorteil kann z.B. auf Standortvorteilen beruhen: Der Kunde zieht einen Friseurladen vor, der in seiner Nachbarschaft liegt. Der Wert hi ist der Preisabstand pi − p , bei dem der Anbieter i keinen Absatz mehr findet. Der optimale Preis pi * kann nunmehr bestimmt werden als (9) a + gi p + hi + gi p* = i = i 2 2 Der Durchschnittspreis aller Anbieter (10) 4 des optimalen Preises pi * nicht berücksichtigt. Dieser Nichtrück-sichtnahme auf die Rückwirkung des eigenen Handelns auf einen allgemeinen Marktparameter entspricht die Annahme im Modell der vollkommenen Konkurrenz, daß der Anbieter seinen Einfluß auf den Marktpreis vernachlässigt. pi − p = h i − b ix i oder (7) © Prof. Dr. C.C. von Weizsäcker p + p +L+ p n p= 1 2 n p h g + + 2 2 2 (11) p$ = wobei h + h +K+ h n h= 1 2 n g + g +K+ g n g= 1 2 n die Durchschnittswerte für die Produktdifferenzierungsvorteile ( h ) bzw. für die Grenzkosten ( g ) darstellen. Wir können uns jetzt vorstellen, daß sich aus einem beliebig vorgegebenen Anfangspreisniveau p( 0 ) mittels der einzelwirtschaftlichen Gewinnmaximierung in der nächsten Periode ein neues Preisniveau p$ = p (1) ergibt: p (1) = wird ja auch vom Preis pi beeinflußt. Da aber die Anzahl n der Anbieter groß ist, ist die Rückwirkung von pi auf p vernachlässigbar klein. Sie wird deshalb beim Festsetzen p (0 ) h + g + 2 2 © Prof. Dr. C.C. von Weizsäcker © Prof. Dr. C.C. von Weizsäcker 5 und so weiter für die folgenden Perioden Schließlich wird ein Gleichgewicht bei normalen Gewinnen erreicht. Sind die Gewinne zuerst unzureichend, kommt es zu Marktaustritt. Dadurch steigen die Gewinne der verbleibenden Anbeiter. Wir können diesen Prozeß modellmäßig abbilden. p (1) h + g + 2 2 p (2 ) h + g p ( 3) = + 2 2 M M M p (2 ) = Es sei (14) Es ist leicht zu sehen, daß dieser Prozeß gegen den Gleichgewichtswert p* konvergiert, der gegeben ist durch die Gleichung (12) 6 p* h + g p* = + 2 2 f + f +K+f n f= 1 2 n der durchschnittliche Wert der Fixkosten. Wir unterstellen, daß dieser Wert sich nicht verändert, wenn sich die Zahl der Anbieter verändert. Dasselbe soll für g gelten. In unserem vereinfachten Modell hängt der Gesamtabsatz im Markt (15) A = x1 + x 2 + K+ x n woraus durch Umformung folgt: (13) nicht vom Preisniveau ab: der Absatz des einzelnen Anbieters schrumpft ja nicht, wenn sein Preis pi und der Durchschnittspreis p um den gleichen Betrag angehoben werden (siehe Gleichung (6)). Die auf die Produkteinheit umgelegte Fixkostenbelastung k ergibt sich im Markt als die Summe der Fixkosten geteilt durch A, also p* = h + g Das gleichgewichtige Preisniveau auf diesem Markt ist die Summe aus durchschnittlichen Grenzkosten und durchschnittlichen Produktdifferenzierungs-vorteilen der im Markt befindlichen Anbieter. (16) k= nf A p$ Sie steigt proportional mit n, der Zahl der Anbieter, da A und f von n unabhängig sind. 45o-Linie h+g Gleichgewichtspunkt h +g 2 p* p Die durchschnittliche Marge m = Preis minus Grenzkosten = p − g muß die Fixkosten pro Stück finanzieren. Sie ist im Gleichgewicht (17) gleich dem durchschnittlichen Produktdifferenzierungsvorteil. Mit steigendem n, d.h. steigender Zahl der Anbieter, wird der durchschnittliche Produktdifferenzierungs-vorteil h kleiner werden. Wenn z.B. der Produktdifferenzierungsvorteil einfach ein Standortvorteil ist, so nimmt dieser mit steigender Ladendichte ab. Es gilt also (18) Wir betrachten nun Markteintritt und Marktaustritt. Wenn in einem Markt gute Gewinne gemacht werden können, werden zusätzliche Anbieter in den Markt kommen. Dadurch wird für jeden einzelnen Anbieter der Absatz kleiner, und die Gewinne schrumpfen. m =p−g = h dm <0 dn © Prof. Dr. C.C. von Weizsäcker 7 Der gleichgewichtige Wert von n, der Zahl der Anbieter, ist da gegeben, wo m = k gilt. Dort reicht die Marge gerade, um die auf die Stückzahl umgelegten Fixkosten zu decken. Ist m > k , so entsteht ein Gewinn, der zu Marktzutritt, also wachsendem n führt. m,k k m n* n Ist m < k , so entstehen Verluste, also Marktaustritt, also sinkendes n. Der gleichg ewichtige Wert für n entspricht dem Schnittpunkt der k -Kurve und der m -Kurve.