Materiewellen, Teilchen als Wellenpaket

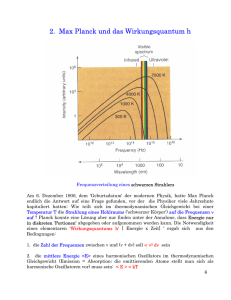
31
Materiewelle wird durch Wellenfunktionen beschrieben
Freies Teilchen V
0 V Potenzial mit gegebenem Impuls p und fester Energie E p2
2m
mit p p Wellenfunktion durch monocharomatische ebene Welle
ψ r t ψ0 exp ik r iω k t = ohne Welle
(3.13)
de Broglie
k
p
E
ω
(3.14)
2m
2m
p2
k2
(3.15)
Analogie zum elektromagnetischen Feld im Vakuum
E
E 0 exp ikr aus
iω k t = ebene Welle für jede Komponente
div E 0 folgt die Bedingung kE 0
0
Die ebene Welle ist unendlich ausgedehnt.
Zu festem Zeitpunkt
y
k
ϕ = ϕ +4 π
0
x
ϕ= ϕ + 2 π
0
Wellenfronten
ϕ = kr − ωt
ϕ=ϕ
0
Abbildung 3.6: Skizze
Übungen Wellenfronten:
Ebenen mit konstanter Phase, ∞-ausgedehnt (z. B. ϕ k r iωt
2π)
(3.16)
32
Abstand Wellenfront mit ϕ ϕ0 und ϕ ϕ0 2π ist
Wellenfront wandert in Richtung von k mit der Phasengeschwindigkeit
∞-Ausdehnung
v phas
2π
λ
ω
k
(3.17)
Idealisierung nicht real
Wahrscheinlichkeitsinterpretation der Wellenfunktion
Elektromagnetisches Feld
Wellenbild:
Pointingvector
S
ε0 xE 2
Energiestromdichte
Energie
Flache Zeit
Teilchenbild:
S
N N ω
Zahl der Protonen
Fläche Zeit
N
ω Energie des Photons
∝ E 2 : Die Anzahl der am Spalt zur Zeit registrierten Photonen ist proportional zum
elektrischen Feld.
Übertragung auf Materialwellen:
ψ r t 2 d 3 r
(3.18)
ψ r t d 3 r 1
(3.19)
ist die Wahrscheinlichkeit, das Teilchen zur Zeit t im Volumenelement d 3 r dx dy dz zu finden.
Sinnvoll nur für ein Ensemble von Teilchen.
Wellenpakete
Eine monochromatische ebene Welle kann kein Teilchen darstellen, dass sich in einem bestimmten
Raumbereich befindet (Lokalisierung).
Beschreibung durch eine Überlagerung von monochromatischen ebenen Wellen Wellenpaket.
ψ x t 1
2π ∞
dk exp i kx ωt ψ̃ k (3.20)
∞
Hier nun eine Dimension betrachtet, der dreidimensionale Fall ist strukturgleich. ψ̃ k : Anzahl und
Phase der am Paket beteiligten m, ebene Wellen im k-Intervall k k dk.
33
Typisches Beispiel: Gauß sches Wellenpaket
ψ̃ k 2σ20
π !
1
4
exp
σ20 k k0 2
c exp σ20 k k0 2
(3.21)
ψ (k)
1
G0
k
0
Abbildung 3.7: Skizze
c
2σ20
π !
1
4
Normierungskonstante
dk ψ̃ k 2 2π
∞
(3.22)
1
(3.23)
k0 : mittlerer Wellenvektor, A k um k0 lokalisiert.
1
σ0 :
Maß für die Breite der Gauß schen Verteilung
Entwicklung der Dispersion
ω k "
ω k0 dω
# dk$% k& k 0
vg
ω0 vg k k 0 vg : Gruppengeschwindigkeit
β: Dispersionsparameter
ψ x t ('
c
2π k0 1 d2ω
k k k0 2 dk2 0
β k k0 ∞
∞
2
2
dk exp )*
σ2 k k0 (3.24)
(3.25)
2
+
34
exp ikx exp ,-
i ) ω0 vg k k0 Übungen Gauß sches Integral
c
exp ) i k0 x ωt 2
/
σ2 iβt
+
exp β k j k0 x vg t 2
4 σ2 iβt 0!
2
+ t.
(3.26)
Wahrscheinlichkeitsverteilung
ψ x t 2 2
2
2
/ 4c 2 2 exp 2σσ4x βv2gtt2 1!
2 σ βt
2
2
/ 4c 2 2 exp 23
2 x vβgt 2
2 G βt
σ 1 σ t 54
2
(3.27)
(3.28)
4
ψ
t=0
ψ (x, 0)|2
ψ (x, t)| 2
zeitliche
σ
0
2 β2 2
G + G2 t
Entwicklung
vg t
Abbildung 3.8: Evolution eines quantenmechanischen Wellenpaketes
σ0 : anfängliche Breite
Das Maximum des Wellenpaketes bewegt sich mit der Gruppengeschwindigkeit.
Das Wellenpaket verbreitert sich (zerfließen). Der Bereich mit einer nennenswerten Wahrscheinlichkeit, ein Teilchen zu finden, wird mit der Zeit immer größer (diffusive Bewegung,
z. B. ...)
typische Verbreiterungszeit
Typische Zeit zum Auseinanderlaufen
τ
β
σ2
β
1 d2ω
2 dk2
(3.29)
(3.30)
35
Photonen:
ω k
β 0 keine Verbreiterung τ ∞
Massebehaftetes Teilchen:
ω
τ
2m
β
σ2
β
k2
∂2 ω
∂k4
m
(3.31)
2m
2mσ2
(3.32)
Je schwerer das Objekt und je größer die anfängliche Ausdehnung, je geringer das Auseinanderlaufen.
Makroskopisches Objekt: m 1g
groß gegenüber Weltalter
σ0
1 cm
Mikroskopisches Objekt: Elektronen, σ 0
10
13
τ 1027 sec
cm
τ 10
26
sec.
Orts-Impuls Unschärferelation
Gegeben P x : Wahrscheinlichkeitsdichte Variable x (Ereignis)
Wir wählen als Ereignisbereich x
67)*
∞ ∞+
Für Wahrscheinlichkeitsdichte gilt die Normierungsbedingung
∞
dxP x 1
∞
Betrachte Gauß sche Wahrscheinlichkeitsdichte
P x 1
exp α x x0 N
2
∆x =
x0
Normierungsfaktor durch Normierungsbedingung gegeben
1
2α
36
1
α x x0 1
exp
N
2
1
N
∞
#∞
$%
αx2 dx exp
&
π
α
98
N
(3.33)
π
a
ā: Erwartungswert oder Mittelwert von x̄
∞
x̄ 9 x "
∞
∞
dx P x x
∞
∞
∞
x0
% & u# $
α x x0 2 x
1
dx exp
N
1
dx x0 exp
N
∞ exp ∞
α x x0 α x x0 N
2
2
∞
#
du 1
∞
1
exp αu2 u
N
$%
&
:
0
x0
(3.34)
∆x: Schwankungsquadrat, “Breite” der Verteilung
∆x x x̄2 ∞
1
2
N
#∞
dx exp
dx P x x x0 α x x0 $%
Gradstein, Ryzlik
α 1
8
π 2α
π
α
1
2α
2
2
x
3 ; 461 :
∆x 1
2α
x0 2
(3.35)
&
π
α
1
2α
(3.36)
Anwendung auf das Gauß sche Paket
1. Im Impulsraum
ψ̃ k P k <
c exp
αk
∆k
2. Im Ortsraum
σ2 k k0 9 ψ̃ k 2 = c 2 exp 2σ2 k k0 2
2
2σ von Zeit unabhängig
1 1 2σ
∆p > ∆k 2αk
2σ
(3.37)
37
P x t = ψ x t 2
α exp
x vg t 2σ2 1 2
τ
t2
ψ (x, 0)|2
ψ (x, t)| 2
∆x (t)
∆x(t) = 0
τ
mσ2
x0 = vg t
αx
∆x
1
1
2σ2
1
2αx
t2
τ
1
8
? @ A
1
σ2 1
t2
τ2
σ8 1 t2
τ2
(3.38)
Produkt aus Orts- und Impulsunschärfe
σ8 1 ∆x∆p
∆x ∆p
B 2
8
1
2
t2 τ2 2σ
t2
τ2
Heisenberg sche Unschärferelation
Am Anfang maximale Schärfe; Auseinanderfließen
Erhöhung der Unschärfe.
(3.39)
(3.40)