Übungsblatt 1 - Universität der Bundeswehr München

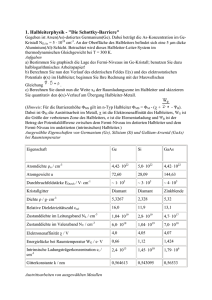
Institut für Physik
Werner-Heisenberg-Weg 39
85577 München / Neubiberg
Fakultät für Elektrotechnik
Universität der Bundeswehr
München / Neubiberg
Prof. Dr. H. Baumgärtner
Übungen: Dr.-Ing. Tanja Stimpel-Lindner, Büro 0118 / G. 37, Tel.: (089) 6004 3192, [email protected]
Physik 2 (B.Sc. EIT)
7. Übungsblatt
X. Festkörperphysik II – Elektronen im metallischen Festkörper
Die Fermi-Verteilung f(W, T) und die Definition des Fermi-Faktors F lauten
f(W, T) =
e
1
W − WF
k B ⋅T
, F=
+1
⎧1, W < WF
.
⎨
⎩0, W > WF
Weiterhin gilt für die Anzahl der freien Elektronen im dreidimensionalen Elektronengas n(W, T) = D(W) ⋅ f(W,T) pro Volumenelement.
D(W) beschreibt dabei die Zustandsdichte in diesem Gas; es gilt
⎛2⋅m
D(W) = 4 ⋅ π ⋅ ⎜
⎜
⎝
h2
3
e
⎞2
⎟
⎟
⎠
⋅
W.
Zur Bearbeitung der folgenden Aufgaben empfiehlt sich ein Studium der folgenden Literatur:
„Physik“ von P.A.Tipler, Seiten 1335 - 1352
Spektrum – Akademischer Verlag, Heidelberg
________________________________________________________________________________________________
Aufgaben
a) Berechnen Sie die Dichte freier Elektronen in Silber und in Gold unter der Annahme eines freien Elektrons pro Atom.
b) Berechnen Sie die Fermi-Energie bei T = 0 K für Kupfer (die Dichte der freien Elektronen in Kupfer bei T = 0 K beträgt 8,47⋅1022 cm-3).
c) Zeigen Sie, dass die Fermi-Dirac-Verteilung f(W, T) für T → 0 in den Fermi-Faktor F übergeht.
d) Schätzen Sie den Anteil freier Elektronen in Kupfer ab, die sich (i) bei Zimmertemperatur und (ii) bei T =1000 K in angeregten Zuständen
oberhalb der Fermi-Energie befinden.
e) Betrachten Sie ein Modell für ein Metall, in dem das Gitter aus positiven Ionen als Behälter für ein klassisches Elektronengas mit n Elektronen pro Volumeneinheit betrachtet wird. Im thermischen Gleichgewicht ist dabei die mittlere Elektronengeschwindigkeit null, und bei
Anlegen eines elektrischen Feldes E werden die Elektronen auf die Driftgeschwindigkeit v beschleunigt. Mit der Relaxationszeit τ aufgrund
der Elektron-Gitter-Stöße der Elektronenmasse m lautet die Bewegungsgleichung der Elektronen
m⋅
dv
dt
+
m
⋅ v = −e ⋅ E .
τ
i) Lösen Sie die Gleichung für die Driftgeschwindigkeit in der Richtung des angelegten elektrischen Feldes.
ii) Verifizieren Sie das Ohmsche Gesetz, und berechnen Sie den spezifischen Widerstand in Abhängigkeit von m, e, n und der
Relaxationszeit τ.
1
XI. Festkörperphysik III – Elektronen im Halbleiter
Zur Bearbeitung der folgenden Aufgaben benötigen Sie nur Ihre Vorlesungsmitschrift und Ihren
Übungsordner der Vorlesung Experimentalphysik II
________________________________________________________________________________________________
In dem folgenden Diagramm ist der spezifische Widerstand der Materialien Silizium, Germanium und Gallium-Arsenid in Abhängigkeit von
der Dotierkonzentration gegeben.
Aufgaben
f) Die Energielücke zwischen dem Valenz- und dem Leitungsband in Silizium beträgt bei Zimmertemperatur 1,14 eV. Wie groß ist die
maximale Wellenlänge eines Photons, das ein Elektron vom oberen Teil des Valenzbandes in den unteren Teil des Leitungsbandes anregen
kann? Was gilt für Germanium?
g) Wie groß ist die Beweglichkeit μn der Elektronen bzw. μp der Löcher in Silizium und in Germanium, wenn das Silizium- bzw. das
Germaniumsubstrat eine konstante n- bzw. p-Dotierung von i) ND/A = 1⋅1016 cm-3, ii) ND/A = 1⋅1017 cm-3, iii) ND/A = 1⋅1018 cm-3, iv) ND/A =
1⋅1019 cm-3, v) ND/A = 1⋅1020 cm-3 besitzt?
h) Tragen Sie μn und μp in Abhängigkeit von der Dotierkonzentration ND bzw. NA für beide Elemente graphisch auf! Was schließen Sie aus
den sich ergebenden Kurvenverläufen?
i) Wird ein Silizium- oder ein Germaniumatom durch ein Arsenatom ersetzt, dann ist ein Elektron der fünf Valenzelektronen des Arsens nur
schwach am Arsenrumpf gebunden. Dieses Elektron sieht damit ein einfach geladenes, anziehendes Ladungszentrum. Die Verhältnisse
ähneln daher denen beim Wasserstoff. Wenn sich ein Elektron in einem Kristall bewegt, lässt sich der Einfluß der anderen Atome
folgendermaßen berücksichtigten: ε0 wird durch εr⋅ε 0 ersetzt und me durch die effektive Masse me* des Elektrons. Für Silizium ist εr = 12,
und die effektive Masse beträgt 0,2⋅me. Für Germanium ist εr = 16, und die effektive Masse beträgt 0,1⋅me. Schätzen Sie im Bohrschen
Atommodell den Bohr-Radius des freien Elektrons des Arsenatoms in Silizium und in Germanium ab!
j) Wie hoch muß man Silizium mit Arsen dotieren, damit sich die Grundzustands-Orbitale der schwach gebundenen Arsenelektronen im Kristall berühren? Was gilt wieder für Germanium?
k) Silizum (Germanium) sei nun so stark mit Arsen dotiert, dass sich die Grundzustands-Orbitale der ungebundenen Arsenelektronen im
Kristall überlappen. Was passiert mit den möglichen Energiezustanden dieser Elektronen im Kristall?
l) Wo liegt bei dieser extremen Arsendotierung das Fermi-Niveau und wie verhält sich die elektrische Leitfähigkeit des so hoch dotierten
Siliziums (Germaniums)?
2
Musterlösung
a) Mit einem freien Elektron pro Atom ist die Anzahldichte der freien Elektronen:
N
n=ρ⋅ A .
mMol
Darin bezeichnet ρ die Dichte des betrachteten Metalls und mMol seine molare Masse. NA ist
die Avogadro-Konstante.
Silber hat die Dichte ρ = 10,5 g⋅cm-3 und die molare Masse mMol = 107,87 g⋅mol-1. Damit
ergibt sich eine Dichte freier Elektronen von n = 5,86⋅1022 cm-3. Für Gold ergibt sich
(ρ = 19,3 g⋅cm-3, mMol = 196,97 g⋅mol-1) n = 5,90⋅1022 cm-3.
b) Die Fermi-Energie im dreidimensionalen Fall bei T = 0 K lässt sich mit der folgenden
Formel berechnen:
2
h2 ⎛ 3 ⋅ N Z ⎞ 3
(*)
WF =
⋅⎜
⎟
8 ⋅ m ⎝ π ⋅V ⎠
Darin bezeichnet h das Plancksche Wirkungsquantum und m die Elektronenmasse. NZ gibt die
Anzahl besetzbarer Zustände im Betrachteten Volumen V im Energieintervall (0, WF]. Bei
T = 0 K besetzen alle vorhandenen freien Elektronen N im Metall genau diese und nur diese
Zustände.
Für die Konzentration freier Elektronen in Kupfer gilt somit bei T = 0 K:
N N
n = = Z = 8,47 ⋅ 10 22 cm − 3 .
V
V
Für Kupfer ergibt sich daraus WF = 7,04 eV.
Herleitung der Beziehung (*)
Im dreidimensionalen Elektronengas ist die Anzahl der freien Elektronen dN pro Volumenelement dV gegeben durch die Beziehung:
dN
n=
= D(W) ⋅ f(W, T) .
dV
D(W) beschreibt die Zustandsdichte. Das ist die Anzahl der besetzbaren Zustände dNZ pro
Volumenelement dV im Energieintervall [W, W + dW] im freien Elektronengas und es gilt:
2
dN Z
⎛ 2 ⋅ m ⎞3
D(W) =
= 4 ⋅π ⋅ ⎜ 2 ⎟ ⋅ W .
dV ⋅ dW
⎝ h ⎠
Wie gezeigt geht f(W, T) für T = 0 K in den Fermi-Faktor F über; damit folgt:
2
dN Z
⎛ 2 ⋅ m ⎞3
n(W, T) = D(W) ⋅ F =
⋅ F = 4 ⋅π ⋅ ⎜ 2 ⎟ ⋅ W ⋅ F .
dV ⋅ dW
⎝ h ⎠
Multipliziert man diese Gleichung mit dW und integriert, dann erhält man:
∞
WF
WF
NZ
V
0
0
0
(da der Fermi-Faktor für W > WF null wird, reicht es, die Integration nur bis WF auszuführen).
Konkret ergibt die Integration:
∫ n(W, T) ⋅ dW = ∫ n(W, T) ⋅ dW = ∫ D(W) ⋅ dW =
3
2
3
WF
N
⎛ 2 ⋅ m ⎞3 2
n(W, T) = D(W) ⋅ F = Z = 4 ⋅ π ⋅ ⎜ 2 ⎟ ⋅ ⋅ W 2
V
⎝ h ⎠ 3
.
0
Setzt man die Integrationsgrenzen ein und löst die Gleichung nach WF auf, dann ergibt sich
die obige Beziehung (*).
c) Die Fermi-Dirac-Verteilung f(W, T) und die Definition des Fermi-Faktors F lauten:
⎧1,W < WF
1
, F =⎨
.
f(W, T) = W −WF
0,
W
W
>
F
⎩
e k B ⋅T + 1
1. Fall W < WF: lim = e
W −W F
k B ⋅T
T →0 K
2. Fall W > WF: lim = e
T →0 K
W −W F
k B ⋅T
= 0 , daraus folgt: F = 1
= ∞ , daraus folgt: F = 0
d)
Die sogenannte Fermi-Temperatur TF wird über die Beziehung WF = kB⋅TF definiert. Die
Fermi-Temperatur von Kupfer beträgt mit WF = 7,04 eV rund TF = 81700 K. Würde man
Kupfer auf diese Temperatur bringen und annehmen, dass der Kupferkristall eine solche
Temperatur übersteht, würden alle (100%) freien Kupferelektronen in energetischen
Zuständen oberhalb der Fermi-Energie sitzen. Für Temperaturen T << TF gleicht die zu T
gehörende Fermi-Verteilung f(W, T) der Fermi-Verteilung f(W, T = 0 K) = F für T = 0 K.
Führt man nun dem Kupferkristall durch Erwärmung auf eine Temperatur T die mittlere
thermische Energie W = kB⋅Τ zu, werden nur die Elektronen im Energieintervall [WF –
kB⋅T, WF] in höhere Energiezustände oberhalb der Fermi-Energie angeregt. Somit kann der
Anteil der Elektronen, die bei einer Temperatur T über das Fermi-Niveau angeregt werden,
folgendermaßen abgeschätzt werden:
100 % 100 %
x
.
=
=
WF
k B ⋅ TF k B ⋅ T
Damit folgt:
T
x = 100 % ⋅
TF
und somit ergibt sich x = 0,367 % (T = 300 K) bzw. x = 1,22 % (T = 1000 K).
e,i) Bei der zu lösenden Differentialgleichung
m
m ⋅ v&(t) + ⋅ v(t) = −e ⋅ E
τ
handelt es sich um eine inhomogene Differentialgleichung erster Ordnung. Diese besitzt
genau eine linear unabhängige Lösung.
Zunächst löst man die homogene Differentialgleichung:
m
m ⋅ v&h (t) + ⋅ vh (t) = 0 .
τ
Als Lösungsansatz wählt man:
4
vh (t) = vD ⋅ eα ⋅t .
Damit folgt:
v&h (t) = α ⋅ vD ⋅ eα ⋅t = α ⋅ vh (t) und m ⋅ v&h (t) +
m
τ
⋅ vh (t) = m ⋅ α ⋅ vh (t) +
m
τ
⋅ vh (t) = 0 .
Ein Koeffizientenvergleich liefert sofort α = − 1τ . Nun bestimmt man eine partikuläre
Lösung vp(t) der inhomogenen Differentialgleichung:
m
m ⋅ v& p (t) + ⋅ v p (t) = −e ⋅ E
τ
mit Hilfe der Methode der unbestimmten Koeffizienten. Da die Störfunktion bzw. das
Restglied R(t) = –e⋅E ein Polynom 0-ten Grades ist (eine Konstante), wählt man als Ansatz
für die partikuläre Lösung ebenfalls ein Polynom 0-ten Grades (eine Konstante): vp(t) = A0 =
konst. Damit ergibt sich:
m
m
v& p (t) = 0 und m ⋅ v& p (t) + ⋅ v p (t) = ⋅ A0 = −e ⋅ E .
Es ist also A0 = −
τ ⋅e⋅ E
m
τ
τ
. Die allgemeine Lösung lautet damit:
v(t) = vh (t) + v p (t) = vD ⋅ e
−
t
τ
−
τ ⋅e⋅ E
m
.
Mit der in der Aufgabenstellung gegebenen Nebenbedingung v(t = 0) = 0 folgt vD =
τ ⋅e⋅ E
m
.
Es ergibt sich also:
τ ⋅ e ⋅ E ⎛⎜
−
⎞
τ ⋅e⋅ E
⋅ ⎜ e τ − 1⎟⎟ und lim v(t) = −vD = −
.
t →∞
m
m
⎝
⎠
Nach einer bestimmten Einschwingzeit t >> τ bewegen sich alle Elektronen kollektiv mit der
konstanten Driftgeschwindigkeit –vD. (Das Minuszeichen gibt an, dass sich die Elektronen
entgegengesetzt zur Richtung des elektrischen Feldes E bewegen.) Man erkennt, dass die
Driftgeschwindigkeit direkt proportional zum elektrischen Feld ist, d. h., je höher das
elektrische Feld ist umso höher ist die Driftgeschwindigkeit. Die Proportionalitätskonstante
τ ⋅e
nennt man Beweglichkeit.
μ=
m
v(t) =
t
ii) Bewegen sich die Elektronen mit der konstanten Geschwindigkeit vD durch einen
elektrischen Leiter der Länge L und der Querschnittsfläche A, dann treten in einem
Zeitintervall dt dN = n⋅A⋅vD⋅dt Elektronen durch die Querschnittsfläche A des elektrischen
Leiters (dabei wird eine konstante Elektronendichte n angenommen). Das entspricht der
Ladung dQ = e⋅dN = n⋅A⋅e⋅vD⋅dt (e bezeichnet darin die Elementarladung). Es fließt also
durch den Leiter der elektrische Strom bzw. die elektrische Stromdichte:
n ⋅ A ⋅τ ⋅ e2
n ⋅ τ ⋅ e2
dQ
I
= n ⋅ A ⋅ e ⋅ vD =
⋅ E bzw. j = = n ⋅ e ⋅ vD =
⋅E
I=
m
m
dt
A
Man erkennt, dass die Stromdichte j direkt proportional zum angelegten elektrischen Feld E
n ⋅τ ⋅ e2
ist. Die Proportionalitätskonstante σ =
nennt man elektrische Leitfähigkeit. Damit
m
folgt für den elektrischen Strom: I = A⋅σ⋅E. Der ohmsche Widerstand des elektrischen Leiters
ist durch
5
L
A
gegeben (ρspezifisch bezeichnet den spezifischen Widerstand des Leitermaterials). Außerdem
gilt für das elektrische Feld:
U
E= .
L
Darin bezeichnet U die über den Leiter der Länge L abfallende elektrische Spannung. Damit
folgt für den elektrischen Strom:
A
I = σ ⋅ ⋅U
L
-1
Da außerdem ρspezifisch = σ gilt, folgt U = R⋅I. (j = σ⋅E bzw. U = R⋅I ist das Ohmsche
Gesetz.)
R = ρ spezifisch ⋅
Mit j = σ⋅E = n⋅e⋅vD und vD = μ⋅E folgt σ = n⋅e⋅μ.
f) Die Energie eines Photons der Frequenz f ist W = h⋅f = h⋅c⋅λ-1. Mit W = 1,14 eV (Größe der
Bandlücke im Siliziumkristall zwischen der Valanzbandoberkante und der Leitungsbandunterkante) folgt für die maximale Wellenlänge des Photons λ = 1,09 μm
(1 eV = 1,6022⋅10-19 J).
Germanium hat eine Bandlücke von W = 0,74 eV, und es folgt λ = 1,77 μm.
g, h) Es gilt das Ohmsche Gesetz j = σ⋅E = n⋅e⋅μ⋅E (darin sind σ ist die elektrische Leitfähigkeit und μ die Beweglichkeit). Aus dem auf dem Aufgabenblatt gegebenen Diagramm
ergeben sich für Silizium und Germanium die folgenden spezifischen Widerstände ρspezifisch
als Funktion der Dotierstoffkonzentration NA bzw. ND.
ND/A [cm-3]
1E16
1E17
1E18
1E19
1E20
ρp-Si [Ω⋅cm]
2
0.35
7Ε-2
1Ε-2
1.5Ε-3
ρn-Si [Ω⋅cm]
5.5Ε-1
9Ε-2
3Ε-2
6E-3
9Ε-4
ρp-Ge [Ω⋅cm]
4E-1
5.5E-2
1E-2
3E-3
6E-4
ρn-Ge [Ω⋅cm]
2.5E-1
4E-2
7E-3
2E-3
4Ε-4
Aus der Beziehung ρn(p)-1 = σ = n⋅e⋅μ = ND,A⋅e⋅μn(p) folgen die Werte für die Beweglichkeiten
μn(p) (μn bezeichnet die Elektronenbeweglichkeit, μp die Löcherbeweglichkeit), die im
folgenden Diagramm in Abhängigkeit von ND(A) für Silizium und Germanium dargestellt sind.
6
-1
2200
Löcher- und Elektronenbeweglichkeiten [cm (Vs) ]
2400
2
2600
p-Typ Silizium
n-Typ Silizium
p-Typ Germanium
n-Typ Germanium
2000
1800
1600
1400
1200
1000
800
600
400
200
0
1E16
1E17
1E18
1E19
1E20
-3
Dotierstoffkonzentration ND(A) [cm ]
i) Im Bohrschen Atommodell (vergleiche mit der Musterlösung zum 3. Übungsblatt, Experimentalphysik II) gilt:
h2
r (Z = 1)
= n2 ⋅ 1
≡ rn (Z)
r(n, Z) = n 2 ⋅ 4 ⋅ π ⋅ ε 0 ⋅
2
Z
m⋅Z ⋅e
Für ein das fünfte ungebundene Valenzelektron des Arsen-Atom im Silizium(Germanium)Kristall gilt Z = 1. Da nach dem Bohrschen Radius gefragt ist gilt n = 1. Mit den notwendigen
Ersetzungen (ε0 → ε rel⋅ε0 und m → m*) ergibt sich rAs, Si = 3,17 nm und rAs,Ge = 8,47 nm.
j) Da die Elementarzelle von Silizium(Germanium) kubisch ist, soll die in der folgenden
Skizze dargestellte Annahme über die Lage der Arsen-Atome in der Elementarzelle gemacht
werden.
Arsen-Atom
Elementarzelle des
Silizium(Germanium)-Kristalls
rAs, Si(Ge)
In einem Volumen V = 8⋅rAs, Si(Ge)3 befindet sich genau ein Arsen-Atom. Damit folgt für die
gesuchten Dotierkonzentrationen NAs, Si = 4⋅1018 cm-3 und NAs, Ge = 2⋅1017 cm-3.
k, l) Erhöht man die in (j) berechneten Dotierkonzentrationen, überlappen sich die Bahnen
der Donatorelektronen und spalten aufgrund des Pauli-Verbots im Kristall zu einem
7
sogenannten Störstellenband auf. Das Fermi-Niveau wird in das Leitungsband des
Siliziums(Germaniums) geschoben. Der leichte Anstieg des spezifischen Widerstandes im
Bereich 5⋅1017 ≤ NAs, Si / cm-3 ≤ 5⋅1019 (1⋅1017 ≤ NAs,Ge / cm-3 ≤ 1⋅1018) lässt sich dadurch
erklären, dass in diesem Bereich die Streuung der freien Elektronen an den Störstellen (den
Dotieratomen) stärker zunimmt. Erst bei noch höheren Dotierungen (dann ist das
Störstellenband voll ausgebildet) bzw. Elektronendichten verliert dieser Streumechanismus an
Dominanz, und der spezifische Widerstand sinkt wieder.
8