∆⋅ о о о = Einheit: 1 kg m/s = 1 Ns

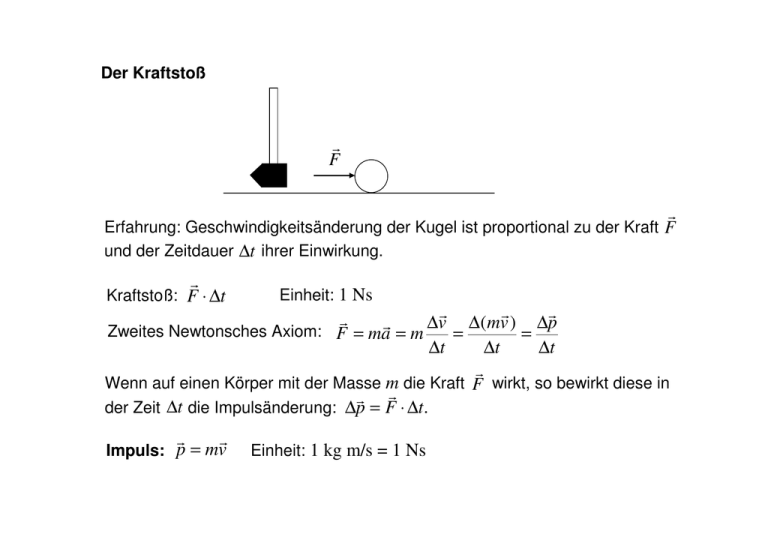
Der Kraftstoß
r
F
r
Erfahrung: Geschwindigkeitsänderung der Kugel ist proportional zu der Kraft F
und der Zeitdauer ∆t ihrer Einwirkung.
r
Kraftstoß: F ⋅ ∆t
Einheit: 1 Ns
r
r
r
r
∆
v
∆
(
m
v
)
∆
p
r
Zweites Newtonsches Axiom: F = ma = m
=
=
∆t
∆t
∆t
r
Wenn auf einen Körper mit der Masse m die Kraft F wirkt, so bewirkt diese in
r r
der Zeit ∆t die Impulsänderung: ∆p = F ⋅ ∆t.
r
r
p
=
m
v
Impuls:
Einheit: 1 kg m/s = 1 Ns
Allgemeinere Form des zweiten Newtonschen Axioms:
r d ( mvr )
Für ∆t → 0 : F =
dt
Wenn die Masse nicht konstant ist, dann muss das zweite Newtonsche Axiom
r
r
r d (mvr )
dv r dm dp
= m +v
=
in der Form F =
angewendet werden.
dt
dt
dt dt
Wenn auf einen Körper mit der Masse m in der Zeit t beliebig viele
r
Kraftstöße F ⋅ ∆t ausgeübt werden, so ist der hierdurch entstehende
r
Impuls p gleich der Summe der Kraftstöße, bzw. das Zeitintegral der
wirkenden Kraft.
r t r
p = ∫ F (t )dt
0
Impulserhaltung
m1
r
v1
r
v2
r
F1
r
F2
m2
m1 m2
r
u1 m
1
m2
r
r
Drittes Newtonsches Axiom: F1 = − F2
r
r
r
r
m1 (u1 − v1 ) = − m2 (u 2 − v 2 )
oder
r
u2
r
r
r
r
∆
p
=
−
∆
p
F1 ⋅ ∆t = − F2 ⋅ ∆t 1
2
r
r
r
r
m1v1 + m2 v2 = m1u1 + m2 u 2
Gesamtimpuls beider Kugeln bleibt erhalten!
Impulserhaltungssatz:
In einem abgeschlossenen System ist die Vektorsumme aller Impulse nach
Betrag und Richtung konstant. Dies gilt auch für nicht reibungsfreie Vorgänge.
Anwendungen: Der Stoß
Grenzfälle:
• Der vollkommen elastische Stoß.
• Der vollkommen unelastische Stoß.
Elastischer Stoß:
• Verformungen der stoßenden Körper werden vollständig rückgängig
gemacht.
• Keine Umwandlung kinetischer Energie z. B. in Wärme, Schall oder
Formänderung.
r
r
m1
r
u1
Es gilt:
v1
v2
m1
m2
m2
r
u2
Energieerhaltung und Impulserhaltung
1
1
1
1
m1v12 + m2 v22 = m1u12 + m2 u 22
2
2
2
2
und
r
r
r
r
m1v1 + m2 v2 = m1u1 + m2 u 2
Zentraler Stoß: Die beiden Körper (z. B. Kugeln) bewegen sich vor und
nach dem Stoß auf derselben Geraden.
r
v1
m1
r
v2
r
u1 m
1
m2
m2
r
u2
Aus Energie- und Impulserhaltung folgt:
Sonderfälle für:
u1 =
2m2 v2 + (m1 − m2 )v1
m1 + m2
u2 =
2m1v1 + (m2 − m1 )v 2
m1 + m2
v2 = 0
2m1
>0
m1 + m2
⇒
u1 =
(m1 − m2 )
2m1
v1 , u 2 =
v1
m1 + m2
m1 + m2
⇒ u 2 hat immer dieselbe Richtung wie v1
Sonderfälle für:
v2 = 0
⇒
(m1 − m2 )
2m1
u1 =
v1 , u 2 =
v1
m1 + m2
m1 + m2
(m1 − m2 )
> 0 ⇒ u1 hat dieselbe Richtung wie v1
1. m1 > m2 ⇒
m1 + m2
r
r
r
u1
v1
u2
m1
m2
m1
m2
2. m1 < m2
⇒
m1
3. m1 = m2
⇒
m1
(m1 − m2 )
< 0 ⇒ u1 hat die entgegengesetzte Richtung wie v1
m1 + m2
r
v1
m2
r
u1
m1
m2
r
u2
(m1 − m2 )
= 0 ⇒ u1 = 0
m1 + m2
r
v1
m2
m1
m2
r
u2
Sonderfälle für:
4. m1 << m2
⇒
m1
m1
r
v1
v2 = 0
⇒
(m1 − m2 )
2m1
u1 =
v1 , u 2 =
v1
m1 + m2
m1 + m2
(m1 − m2 )
≈ −1 ⇒ u1 ≈ −v1 und
m1 + m2
m2
r
v1
r
u1
m1
u2 ≈ 0
m2
r
u1 m
1
kein Energieübertrag
Impulsübertrag auf die Wand: ∆p = m1u1 − m1v1 = m1u1 + m1u1 = 2m1u1
5.
m1 << m2 Stoß ist nicht zentral!
r
Zerlegung von v1 in die Komponenten
r
v1
v
v
v x und v y
v
v y bleibt unbeeinflusst, vrx → −vrx
r
vy
r
u1
kein Energieübertrag auf die Wand
v
Impulsübertrag: 2mv x
Sonderfall:
Beide Kugeln sind vor dem Stoß in Bewegung und haben die gleiche Masse
u1 =
2m2 v2 + (m1 − m2 )v1
= v2
m1 + m2
u2 =
2m1v1 + (m2 − m1 )v 2
= v1
m1 + m2
Die beiden Körper tauschen ihre
Geschwindigkeiten und damit
ihre kinetischen Energien aus.
Unelastischer oder plastischer Stoß:
• keine elastischen Kräfte Körper bleiben nach dem Stoß zusammen
• Formänderungen bleiben vollständig erhalten
Die kinetische Energie bleibt nicht erhalten!
r
r
r
r
r m1 v1 + m 2 v 2
Es gilt Impulserhaltung: m1 v1 + m 2 v 2 = ( m1 + m 2 )u ⇒ u =
( m1 + m 2 )
Umgewandelte kinetische Energie:
Sonderfall: Zentraler Stoß
1
1
1
∆Ekin = m1v12 + m2 v22 − ( m1 + m2 )u 2
2
2
2
 m v + m2 v 2 
1
1
1

= m1v12 + m2 v22 − (m1 + m2 ) 1 1
2
2
2
 ( m1 + m2 ) 
⇒ ∆Ekin
m1m2 (v1 − v2 )
=
2(m1 + m2 )
2
mit
2
m1 = m2 = m und
v1 = v = − v 2
Impulserhaltung: u = 0
Umgewandelte Energie:
∆Ekin
∆Ekin
m 2 ⋅ 4v 2
=
= mv 2
4m
1
= 2 ⋅ mv 2
2
Der Massenmittelpunkt oder Schwerpunkt:
m1
x1
xS
m2
x2
x
Die Koordinate des Massenmittelpunktes xS wird definiert durch:
m1 x1 + m2 x2
m ges
Beispiel: m1 = m2 , x1 = 2cm , x 2 = 6cm xS = 4cm
( m1 + m2 ) x S = m1 x1 + m2 x2 ⇒ x S =
Für N Teilchen, die sich im dreidimensionalen Raum befinden gilt:
N
N
r
r
r
r
r
r
m ges rS = ∑ mi ri mit rS = x S e x + y S e y + z S e z d.h.: m ges xS = ∑ mi xi ,
i =1
i =1
N
Für einen kontinuierlichen Körper:
r
r
m ges rS = ∫ r dm
m ges y S = ∑ mi yi ,
i =1
N
m ges z S = ∑ mi z i
i =1
Beispiel homogener Stab:
y
z
x
x
x=l
dx
dx m ges
dm = m ges
=
dx
l
l
l
m ges
m ges l
m ges  1 2  l
m ges x S = ∫ xdm = ∫ x
dx =
xdx =
x 
∫

l
l 0
l 2 0
0
m ges 1 2 m ges l
l
⇒ m ges x S =
l =
⇒ xS =
l 2
2
2
Beschleunigung des Massenmittelpunktes:
N
r
r
m ges rS = ∑ mi ri
i =1
m ges
r
r
N
d 2 rS N
d 2 ri
r
r
=
m
⇒
m
a
=
m
a
∑
∑
i
ges S
i i
dt 2
dt 2
i =1
i =1
Newton: Resultierende Kraft auf das i-te Teilchen:
r
r
r
r
Fi = mi ai = Fi (intern ) + Fi (extern )
N
N r
N r
r
r
einsetzen: m ges a S = ∑ mi ai = ∑ Fi (intern) + ∑ Fi (extern)
i =1
i =1
i =1
Drittes Newtonsches Axiom: Die internen Kräfte die die Teilchen wechselseitig
aufeinander ausüben heben sich gegenseitig auf!
N r
r
⇒ Fext = ∑ Fi (extern) = m ges a S
i =1
Der Massenmittelpunkt eines Systems bewegt sich unter dem Einfluss der
N
resultierenden äußeren Kraft wie ein Teilchen mit der Masse m ges = ∑ mi .
i =1
Bei einem abgeschlossenen System von Massenpunkten, d.h. einem
System auf das keine äußeren Kräfte wirken, befindet sich der Schwerpunkt
in Ruhe oder er behält seine Geschwindigkeit (nach Betrag und Richtung)
unverändert bei.
Beispiel: Bombe
S
• Der Schwerpunkt ist vor und nach der Explosion in Ruhe.
• Der Gesamtimpuls ist vor und nach der Explosion Null.
Der Schwerpunktsatz und der Impulserhaltungssatz sind gleichwertig!
Beispiel: Unterstützung im Schwerpunkt
P
F1
PS
=
FHilfs
x1
Beispiel:
starrer Körper
und
F2
PS
=
FHilfs x2
⇒ F1 x1 = F2 x2
⇒ m1 x1 = m2 x2
r
r r
FR = F1 + F2
r
− FHilfs
x1
r
F1 = m1 g
S
r
FHilfs
x2
r
F2 = m2 g
r
r r
FR = F1 + F2
Der Körper ist im
r
Gleichgewicht, wenn FR
kompensiert wird.
Weitere Beispiele für die Impulserhaltung:
• Ein Mensch springt von einem ruhig am Ufer liegenden Boot an Land.
Das Boot bewegt sich nach hinten.
• Fortbewegung eines Tintenfisches: Er stößt Wasser aus und bewegt sich
in die Gegenrichtung.
• Bewegung von Raketen: Verbrannter Treibstoff erhält einen rückwärts
gerichteten Impuls, die Rakete einen gleich großen Impuls nach vorne.
• Bewegung von Propellerflugzeugen: Die Luft erhält einen Impuls nach
hinten, das Flugzeug einen gleich großen Impuls nach vorne.
• Rückstoß beim Abschießen eines Gewehres
• Bewegung eines Menschen auf der Erde.
Impulserhaltungssatz

3. Newtonsches Axiom
Übungen
• Gibt es dreidimensionale Körper, die an ihrem Massenmittelpunkt keine Masse
enthalten?
• Ein Kind springt von einem kleinen Boot an Land. Sein Zwilling springt über
einen Graben. Welche Aussage stimmt?
a) Das Kind muss mit mehr Energie springen als sein Zwilling.
b) Sein Zwilling muss mehr Energie aufbringen als es selbst.
c) Beide müssen gleich viel Energie aufbringen.
•
Betrachten Sie einen vollkommen unelastischen Stoß zwischen zwei
Kugeln gleicher Masse. Wann ist der Verlust an kinetischer Energie größer?
a) Wenn sich die beiden Kugeln jeweils mit dem Geschwindigkeitsbetrag
v/2 nähern.
b) Wenn eine Kugel ruht und die andere den Geschwindigkeitsbetrag v hat.
c) Der Verlust an kinetischer Energie ist in beiden Fällen gleich groß.
• Ein Pendelgewicht schwingt hin und her. Welche Aussage
stimmt?
a) Sein Impuls ist zeitlich konstant.
b) Sein Impuls ändert sich.
• Das Bild zeigt ein Geschoss unmittelbar nach dem Zerbrechen
in drei
Stücke. Wie schnell war das Geschoss in dem Moment, bevor es
zerbrochen ist?
(v1 + v2 + v3 ) / 4 ?
v 2 = 2v1
v3
m
m
(v1 + v2 + v3 ) / 3 ?
v3 / 4 ?
v3 / 3 ?
2m
v1
v3 ?