B-Feld um
Werbung

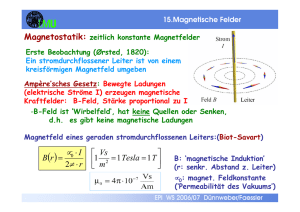
19. Vorlesung EP III Elektrizität und Magnetismus 19. Magnetische Felder (Magnetostatik) Versuche: Feldlinienbilder (B-Feld um Einzeldraht, 2 Drähte, Spule) Kraftwirkung von Strömen Drehspulinstrument Fadenstrahlrohr EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Magnetostatik: zeitlich konstante Magnetfelder Ein stromdurchflossener Leiter ist von einem kreisförmigen Magnetfeld umgeben (Ørsted, 1820) Bewegte Ladungen (elektrische Ströme) erzeugen magnetische Kraftfelder: B-Feld - B-Feld ist ‘Wirbelfeld‘, hat keine Quellen oder Senken - es gibt keine magnetische Ladung (Ampère’sches Gesetz) In einer Spule addieren sich die Felder benachbarter Drähte vektoriell. Es ergibt sich eine im Vergleich zum Einzeldraht höhere Feldliniendichte im Inneren der Spule, die annähernd homogen ist. Mit Eisenfeilspänen läßt sich das magnetische Kraftfeld sichtbar machen. EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Stabmagnete (Permanentmagnete) EP WS 2007/08 Dünnweber/Faessler Magnetische Kraft zwischen zwei stromdurchflossenen Leitern I1 r F F I2 x r r anziehende Kraft für parallele I1 , I2 (abstoßende für antiparallele r r I ,I ) 1 2 F= µ0 I ⋅I ⋅x⋅ 1 2 2π r mit „magnetischer Feldkonstante“ V ⋅s N µ 0 = 4π ⋅10 −7 2 = A ⋅ m A In Analogie zur Elektrostatik definiert man eine Feldstärke µ I B= 0 ⋅ 2π r Die B-Feldstärke nennt man „magnetische Induktion“. Sie hat die Einheit V ⋅s m 2 = T(" Tesla" ) EP WS 2007/08 Dünnweber/Faessler H = B/µ0 heißt „magnetische Feldstärke“, Einheit A m (Manchmal wird auch B als magnetische Feldstärke und H als magnetische Erregung bezeichnet.) Im Beispiel zweier stromdurchflossener Leiter (s.o.): B= µ 0 I1 ⋅ 2π r (B-Feld um I1 im Abstand r) →F = B · I2 · x (Kraft auf Leiter 2) r Allgemein ist die Kraft auf einen Leiter im B-Feld für B senkrecht r auf Leiterstrecke x : F=B·I·x (Obige Beziehungen gelten im Vakuum und in guter Näherung auch in Luft, in Materie (→nächste Vorlesung) ist B = µrelativ · BVakuum) EP WS 2007/08 Dünnweber/Faessler Kraft zwischen parallelen, stromdurchflossenen Leitern r ∆F ∆x = I ⋅B µ0 ⋅ I B(r ) = 2π ⋅ r µ0 ⋅ I 2 ∆F =± ∆x 2π r Kraft F ist anziehend, wenn Ströme parallel, abstoßend, wenn Ströme entgegengesetzt Basiseinheit 1 Ampere: (alternative Definition zu 1A = 1 C/s) Wenn 2 parallele Leiter im Abstand r=1 m von je 1 A durchflossen werden, dann wirkt eine Kraft von 2.10-7 N pro Meter. EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Magnetfeld einer (langen) Spule: N B = µ0 ⋅ I ⋅ L N = Windungszahl, L = Spulenlänge Magnetisches Dipolfeld: - Feldlinien zeigen vom Nord- zum Südpol - Bezeichnung aufgrund der Ausrichtung der Kompassnadel (Nordpol der Kompassnadel zeigt nach Norden) - Dipolfeld wie bei Spule EP WS 2007/08 Dünnweber/Faessler EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Richtung des Magnetfeldes r r r sind B und H(= B / µ 0 ) Vektoren. Ihre Richtung ergibt sich aus der „RechteHand-Regel“. (Der Strom r r I oder j hat dieselbe r Richtung wie der Leiter l ). Richtung der Kraft auf stromdurchflossenen Leiter r r r F = I⋅ l x B I r l r r r d.h. F steht senkrechtrauf l und B (im Fall der Skizze zeigt F in die Zeichenebene) EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Auf einen stromdurchflossenen Leiter der Länge l wirkt im Magnetfeld eine Kraft F: r r r dF = I ⋅ dl × B EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Verwendung zur Strommessung: Amperemeter: Drehspulinstrument (Galvanometer) EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Kraft auf Ladung in elektr. u. magnet. Feldern: Lorentz-Kraft: ( r r r r F = Q⋅ E + v×B ↑ Ladung ) ↑ Geschwindigkeit d. Ladung beachte: die von der mit v bewegten Ladung erzeugten Felder werden bei E, B nicht mitgezählt. Lorentzkraft auf Ladung ∆Q: r ∆ F = ∆Q ⋅ v ⋅ B Aus ∆Q ⋅ v = I ⋅ ∆x falls Geschwindigkeit v senkrecht zum B-Feld folgt Lorentzkraft pro 1m Leiter: r ∆F ∆x = I ⋅B EP WS 2007/08 Dünnweber/Faessler 19. magnetische Felder Ablenkung von Elektronenstrahlen im Magnetfeld (Fadenstrahlröhre): -> im Magnetfeld B werden Elektronen auf einer Kreisbahn abgelenkt Kräftegleichgewicht: FZ = FL damit: v 02 ⇒ m ⋅ = e ⋅ v0 ⋅ B R e v = 0 m R ⋅B Ablenkradius: oder: e 2 ⋅U = 2 2 m R ⋅B m ⋅ v0 R= e⋅B Umlauffrequenz: ω = v0 v0 e ⋅ B = R m (Zyklotronfrequenz) EP WS 2007/08 Dünnweber/Faessler