Das Magnetische Feld eines stromdurchflossenen Kreisringes…

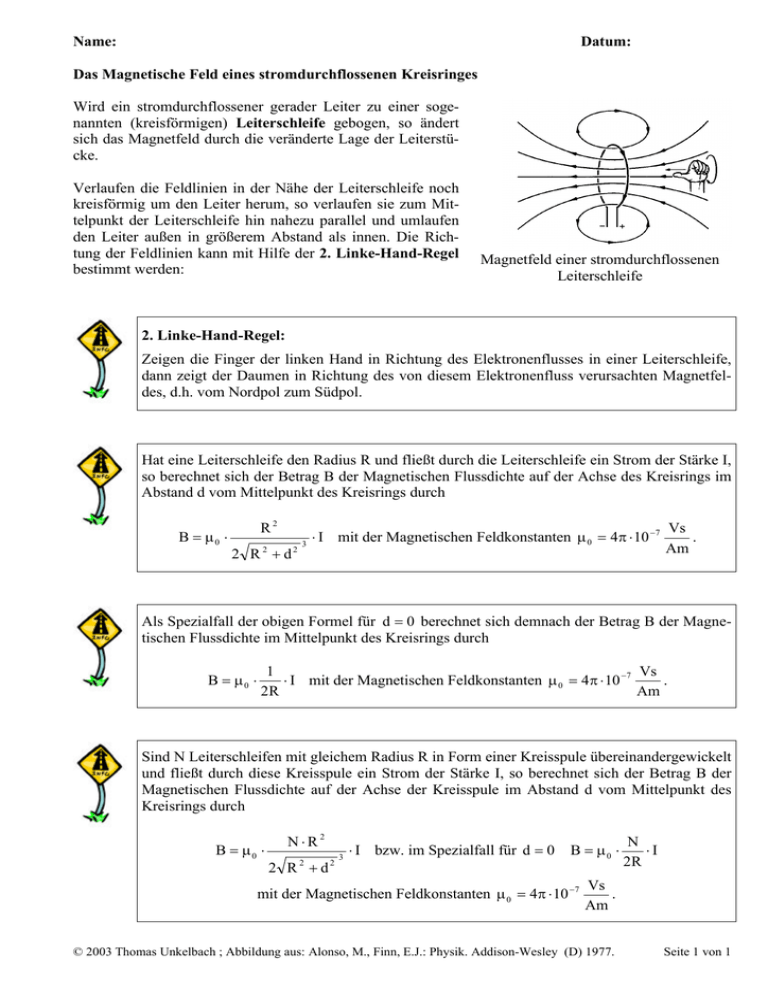
Name:
Datum:
Das Magnetische Feld eines stromdurchflossenen Kreisringes
Wird ein stromdurchflossener gerader Leiter zu einer sogenannten (kreisförmigen) Leiterschleife gebogen, so ändert
sich das Magnetfeld durch die veränderte Lage der Leiterstücke.
Verlaufen die Feldlinien in der Nähe der Leiterschleife noch
kreisförmig um den Leiter herum, so verlaufen sie zum Mittelpunkt der Leiterschleife hin nahezu parallel und umlaufen
den Leiter außen in größerem Abstand als innen. Die Richtung der Feldlinien kann mit Hilfe der 2. Linke-Hand-Regel
bestimmt werden:
Magnetfeld einer stromdurchflossenen
Leiterschleife
2. Linke-Hand-Regel:
Zeigen die Finger der linken Hand in Richtung des Elektronenflusses in einer Leiterschleife,
dann zeigt der Daumen in Richtung des von diesem Elektronenfluss verursachten Magnetfeldes, d.h. vom Nordpol zum Südpol.
Hat eine Leiterschleife den Radius R und fließt durch die Leiterschleife ein Strom der Stärke I,
so berechnet sich der Betrag B der Magnetischen Flussdichte auf der Achse des Kreisrings im
Abstand d vom Mittelpunkt des Kreisrings durch
B = µ0 ⋅
R2
2 R 2 + d2
3
⋅ I mit der Magnetischen Feldkonstanten µ 0 = 4π ⋅ 10 −7
Vs
.
Am
Als Spezialfall der obigen Formel für d = 0 berechnet sich demnach der Betrag B der Magnetischen Flussdichte im Mittelpunkt des Kreisrings durch
B = µ0 ⋅
1
Vs
⋅ I mit der Magnetischen Feldkonstanten µ 0 = 4π ⋅ 10 −7
.
2R
Am
Sind N Leiterschleifen mit gleichem Radius R in Form einer Kreisspule übereinandergewickelt
und fließt durch diese Kreisspule ein Strom der Stärke I, so berechnet sich der Betrag B der
Magnetischen Flussdichte auf der Achse der Kreisspule im Abstand d vom Mittelpunkt des
Kreisrings durch
B = µ0 ⋅
N⋅R2
2 R 2 + d2
3
⋅ I bzw. im Spezialfall für d = 0
B = µ0 ⋅
mit der Magnetischen Feldkonstanten µ 0 = 4π ⋅ 10 −7
N
⋅I
2R
Vs
.
Am
© 2003 Thomas Unkelbach ; Abbildung aus: Alonso, M., Finn, E.J.: Physik. Addison-Wesley (D) 1977.
Seite 1 von 1