3. Vorlesung

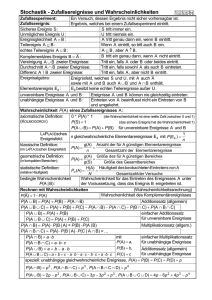
Grundbegriffe
Zufallsexperiment
Verknüpfungen
Das Verknüpfen von Ereignissen entspricht den Operationen mit Mengen.
unter gleichen Bedingungen zumindest gedanklich
beliebig oft wiederholbarer Vorgang
Menge der möglichen Versuchsausgänge ist bekannt
konkreter Ausgang ist ungewiss (zufällig)
Ereignis A ∪ B (Vereinigung) tritt ein,
wenn mindestens eins der Ereignisse A,
B eintritt.
Grundraum/
Ereignisraum Ω
Menge aller möglichen einander ausschließenden
Versuchsausgänge
Elementarereignis ω
jede einelementige Teilmenge von Ω
Ereignis
Menge von Versuchsausgängen/Elementarereignissen,
Teilmenge von Ω
Ereignis A ∩ B (Durchschnitt) tritt ein,
wenn beide Ereignisse A, B eintreten.
Ereignis A \ B (Differenz) tritt ein,
wenn A eintritt, B nicht eintritt.
Ein Ereignis A tritt ein, wenn der beobachtete Versuchsausgang ω ein Element
von A ist.
Das Ereignis Ω ist das sichere Ereignis, das stets eintritt.
Die leere Menge ∅ bezeichnet das unmögliche Ereignis, das nie eintritt.
SS 2016
Prof. Dr. J. Schütze, FB GW
3.1
Wkt.1
1
Verknüpfungen
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
2
Wkt.1
4
Rechenregeln für Mengenverknüpfungen
Die Mengenoperationen Vereinigung und Durchschnitt entsprechen den
Operationen der Aussagenlogik und folgen deren Gesetzen:
∩ entspricht 'und' bzw. logischem Symbol ∧,
∪ entspricht 'oder' bzw. logischem Symbol ∨.
Komplementärereignis A tritt genau dann ein,
wenn A nicht eintritt.
Es gelten folgende Gesetze:
Zwei Ereignisse A, B heißen unvereinbar
oder disjunkt, wenn sie keine gemeinsamen
Elementarereignisse besitzen, A ∩ B = ∅.
Ereignis A zieht Ereignis B nach sich,
wenn A ⊆ B gilt.
Kommutativität:
A ∩ B = B ∩ A, A ∪ B = B ∪ A
Assoziativität:
( A ∩ B) ∩ C = A ∩ ( B ∩ C )
( A ∪ B) ∪ C = A ∪ ( B ∪ C )
Distributivität:
A ∩ ( B ∪ C ) = ( A ∩ B) ∪ ( A ∩ C )
A ∪ ( B ∩ C ) = ( A ∪ B) ∩ ( A ∪ C )
Regeln von de Morgan
A∪ B = A∩ B
3.2
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
3
SS 2016
A∩ B = A∪ B
Prof. Dr. J. Schütze, FB GW
Wahrscheinlichkeitsbegriffe
Wahrscheinlichkeitsbegriffe
Empirisches Gesetz der großen Zahlen
‚Zufall' von Ereignissen misst man, indem man den Ereignissen sinnvoll
eine Zahl zuordnet, die der Chance ihres Eintretens entspricht.
Diese Zahl nennt man Wahrscheinlichkeit.
Beispiel 1
Eine bestimmte Sorte von Energiesparlampen erreicht in bisherigen Beobachtungen
mit einem Anteil von 10% die Brenndauer von 4000 h nicht.
Man sagt, die Wahrscheinlichkeit, dass die Brenndauer < 4000 ist, liegt bei 0.10.
Solche Aussagen beruhen auf der Analyse der Brenndauern in der Vergangenheit.
Die beobachtete relative Häufigkeit wird als (geschätztes) Maß für die
Wahrscheinlichkeit des Ausfalls vor 4000 h genommen.
Relative Häufigkeiten (beobachtet) beziehen sich auf den Anteil in der Stichprobe,
Wahrscheinlichkeiten (Modell) beziehen sich auf die Grundgesamtheit.
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
5
Voraussetzungen:
nur endlich viele Elementarereignisse
alle mit gleicher Chance (z.B. idealer Würfel)
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
6
Permutationen ohne Wiederholung
Für n verschiedene Objekte gibt es genau
n!
Definition
Wahrscheinlichkeit für Eintreten des Ereignisses A ⊆ Ω
Möglichkeiten der Anordnung, wenn jedes Element genau einmal verwendet wird.
Kombinationen ohne Wiederholung
Aus einer n-elementigen Menge verschiedener Objekte werden k ausgewählt
ohne Wiederholung
ohne Berücksichtigung der Reihenfolge.
Anzahl der Elementarereignisse von A A
=
Anzahl der Elementarereignisse von Ω Ω
Wahrscheinlichkeiten nach Laplace können somit durch Auszählen
der Elementarereignisse berechnet werden.
Für komplizierte Sachverhalte braucht man kombinatorische Formeln.
Man erhält für die Anzahl solcher k-elementigen Teilmengen
3.3
Prof. Dr. J. Schütze, FB GW
Nachteil: die Folge der hn stabilisiert sich nicht immer zu einem Grenzwert
Zählprinzip
Menge M enthalte m verschiedene, Menge N enthalte n verschiedene Elemente.
Dann enthält M × N genau m·n verschiedene Elemente (geordnete Paare).
Laplace: 1749-1824
SS 2016
Dieser experimentelle Zugang zur Bestimmung von Wahrscheinlichkeiten
liefert 'nur' Schätzwerte (im realen Experiment ist n stets endlich).
Bezeichnung: Experimentelle/ statistische Wahrscheinlichkeit
Kombinatorische Formeln (Auswahl)
Wahrscheinlichkeit nach Laplace
P ( A) =
Wird ein Zufallsexperiment zur Beobachtung eines Ereignisses A n-mal
unter gleichen Bedingungen wiederholt, dann stabilisieren sich die
relativen Häufigkeiten
1
hn ( A) = ⋅ (Anzahl des Auftretens von A)
n
für n → ∞
zu einem Grenzwert, der Wahrscheinlichkeit P(A).
Wkt.1
7
n
n!
genau   =
Möglichkeiten.
k
k
!(
n
− k )!
 
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
8
Geometrische Berechnung von Wahrscheinlichkeiten
Interpretation
Nicht immer liegen nur endlich viele Elementarereignisse vor.
Interpretation der Wahrscheinlichkeit
Beispiel 2
• Wahrscheinlichkeit p als Chance des Eintretens eines zufälligen Ereignisses:
0≤p≤1
Gesucht ist Wahrscheinlichkeit, auf einer kreisförmigen Schießscheibe zufällig ins
Schwarze zu treffen. Voraussetzung ist, dass die Scheibe überhaupt getroffen wird.
Die Scheibe bestehe aus 10 konzentrischen Kreisen mit gleichem Zuwachs der
Radien, die kleinste davon ist der schwarzer Kreis.
• Wert p sagt nichts über den Ausgang eines konkreten Versuchs
• In langen Versuchsserien unter gleichen Bedingungen stabilisiert sich der Anteil
der Experimente, in denen A eintritt,
daraus ergibt sich die Möglichkeit der Näherung der Wahrscheinlichkeit von A
durch die relative Häufigkeit
Die Ergebnismenge Ω ist hier die Menge aller Punkte der Scheibe, also
überabzählbar unendlich, damit ist ein Auszählen von Ereignissen nicht möglich.
Die Berechnung der Wahrscheinlichkeit nach Laplace funktioniert also nicht.
Ausweg: Man setzt die Fläche A des gesuchten Ereignisses
ins Verhältnis zur Fläche der Ergebnismenge und erhält
Fläche A = r 2 ⋅ π, Gesamtfläche G = (10r ) 2 ⋅ π
A
r 2π
1
P ( A) = =
=
G 100r 2 π 100
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
9
Axiomatischer Wahrscheinlichkeitsbegriff
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
10
Wkt.1
12
Wahrscheinlichkeitsbegriffe
Die folgenden Axiome gehen zurück auf Kolmogorov.
Sie sind verträglich mit der Laplace- und der statistischen Wahrscheinlichkeit,
und sie gelten auch bei Modellen mit unendlich vielen Versuchsausgängen.
(1) Wahrscheinlichkeit nach Laplace-Modell
Voraussetzungen:
nur endlich viele Elementarereignisse
alle mit gleicher Chance (z.B. idealer Würfel)
Axiom 1
Jedem zufälligen Ereignis A ⊆ Ω ist eine Zahl P(A) zugeordnet mit
0 ≤ P ( A) ≤ 1 , die man Wahrscheinlichkeit von A nennt.
(2) Statistische/experimentelle Wahrscheinlichkeit
1
P( A) ≈ ⋅ ( Anzahl des Auftretens von A) für n → ∞
n
Axiom 2
Das sichere Ereignis hat die Wahrscheinlichkeit 1.
P (Ω ) = 1
(3) Axiomatische Definition der Wahrscheinlichkeit nach Kolmogorov
Axiom 3
Für disjunkte Ereignisse A1 ∩ A2 = ∅ gilt
P ( A1 ∪ A2 ) = P ( A1 ) + P ( A2 )
Bei einer unendlichen Ergebnismenge ist Axiom 3 auf unendlich viele paarweise
disjunkte Mengen zu erweitern:
∞  ∞
Die nach Laplace-Modell berechneten bzw. experimentell gewonnenen
Wahrscheinlichkeiten sind konform zu den Axiomen von Kolmogorov.
P   Ai  =  P( Ai )
 i=1  i =1
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
11
SS 2016
Prof. Dr. J. Schütze, FB GW
Rechnen mit Wahrscheinlichkeiten
Bedingte Wahrscheinlichkeit und Unabhängigkeit
Beispiel 3
Rechengesetze
Sicheres Ereignis Ω
Unmögliches Ereignis Ø
Monotonie
Additionssatz
Spezialfall: disjunkte
Ereignisse
Spezialfall: Ω diskret
Komplementäres Ereignis
Differenz
Lostrommel enthalte 500 Lose, davon seien 200 weiß, die restlichen 300 blau.
Unter den weißen Losen seien 10 Gewinne, unter den blauen seien 20 Gewinne.
Welche Losfarbe würden Sie nach dieser Kenntnis ziehen?
P (Ω) = 1
P (∅) = 0
A ⊂ B → P ( A) ≤ P ( B )
P ( A ∪ B ) = P ( A) + P ( B ) − P ( A ∩ B )
W: zufällig gezogenes Los weiß
B: zufällig gezogenes Los blau
G: zufällig gezogenes Los ist ein Gewinn
P ( A ∪ B ) = P ( A) + P ( B ), falls A ∩ B = ∅
P ( A) = Σ P (ω)
ω∈A
P ( A) = 1 − P ( A)
P ( A \ B ) = P ( A) − P ( A ∩ B )
P(G) = 30/500 = 0.06
Nur weiße Lose
Nur blaue Lose
G∩W : Los ist weiß und ein Gewinn
G∩B :
P(G∩W) = 10/500 = 0.02
P(G∩B) = 20/500 = 0.04
P(B) = 300/500 = 0.6
P(W) = 200/500 = 0.4
3.4
Gewinnchance P (G ∩ W ) = 10 / 500 = 0.05
P (W )
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
13
Bedingte Wahrscheinlichkeit
Los ist blau und ein Gewinn
Gewinnchance
200 / 500
SS 2016
Prof. Dr. J. Schütze, FB GW
P (G ∩ B ) 20 / 500
=
= 0.06
P( B)
300 / 500
Wkt.1
14
Totale Wahrscheinlichkeit
Aus den bedingten Wahrscheinlichkeiten erhält man die Gewinnwahrscheinlichkeit
P (G ) = P (G ∩ W ) + P (G ∩ B ) = P (G / W ) ⋅ P (W ) + P (G ∩ B ) ⋅ P ( B )
Bedingte Wahrscheinlichkeit eines Ereignisses A unter der Bedingung B
P( A ∩ B)
P( A / B) =
P( B)
= 0.05 ⋅ 0.4 + 0.067 ⋅ 0.6 = 0.06
Satz der totalen Wahrscheinlichkeit
Dabei ist A, B ⊆ Ω und P ( B ) > 0
Ω = B1 ∪ B2 ∪ ... ∪ Bn , alle Bk seien paarweise disjunkt
Dann gilt
Interpretation
Die Berechnung einer bedingten Wahrscheinlichkeit bedeutet die Einschränkung
der gesamten Ergebnismenge Ω auf die durch die Bedingung definierte
Teilmenge B der gesamten Ergebnismenge Ω .
Gewinnchance unter der Bedingung ‚blau‘:
Gewinnchance unter Bedingung ‚weiß‘:
SS 2016
Gewinnchance ohne Farbinfo
P (G ∩ B )
P (G / B ) =
= 0.06
P( B)
P (W ∩ B )
P (G / W ) =
= 0.05
P( B)
Prof. Dr. J. Schütze, FB GW
Wkt.1
15
n
P ( A) =  P ( A / Bk ) ⋅ P ( Bk )
k =1
Bedeutung des Satzes
Das Ereignis A kann zunächst in Subpopulationen Bk beobachtet werden,
der Satz der totalen Wahrscheinlichkeit ermöglicht daraus die Berechnung der
Wahrscheinlichkeit für die Gesamtpopulation.
Es erfolgt dabei eine Wichtung der Subpopulationswahrscheinlichkeiten mit dem
Anteil der Subpopulation an der Gesamtpopulation.
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
16
Bedingte Wahrscheinlichkeit
Totale Wahrscheinlichkeit
Beispiel 4
Eine Fußballmanschaft spielt mit 2 Stürmern A und B.
Von Stürmer A kommen 50% aller Schüsse auf das Tor, Trefferwahrscheinlichkeit 70% .
Von Stürmer B kommen 40% aller Schüsse auf das Tor, Trefferwahrscheinlichkeit 80% .
Die restlichen Spieler R haben eine Trefferwahrscheinlichkeit von 30%.
Alternativ:
Berechnung mit Pfaddiagramm
a) Mit welcher Wahrscheinlichkeit ist ein Schuss auf das Tor ein Treffer?
b) Mit welcher Wahrscheinlichkeit wurde ein Treffer von Stürmer B erzielt?
Ergebnismenge Ω : alle Schüsse auf das Tor
Ereignis T :
Schüsse auf das Tor, die ein Treffer sind
Ereignisse A, B, R: Schüsse auf das Tor von Stürmer A, B bzw. vom Rest
P(A) = 0.5
P(B) = 0.4
P(R) = 0.1
Aufbau eines Pfaddiagramms
Wahrscheinlichkeiten nach einem Knoten summieren sich stets zu 1.
Pfad symbolisiert den Durchschnitt der Ereignisse, die er durchläuft.
Pfadwahrscheinlichkeit = Produkt der Wahrscheinlichkeiten entlang des Pfads, z.B.
P( A) ⋅ P (T / A) = P( A ∩ T )
P(T/A) = 0.7 Trefferwahrscheinlichkeit von A
P(T/B) = 0.8 Trefferwahrscheinlichkeit von B
P(T/R) = 0.3 Trefferwahrscheinlichkeit von R
Wahrscheinlichkeit eines Endereignisses =
Summe aller Pfadwahrscheinlichkeiten zu diesem Endereignis, z.B.
P(T ) = P (T / A) ⋅ P( A) + P(T / B) ⋅ P( B) + P(T / C ) ⋅ P(C )
Satz der totalen Wahrscheinlichkeit
P (T ) = P (T / A) ⋅ P ( A) + P (T / B ) ⋅ P ( B ) + P (T / R ) ⋅ P ( R )
P (T ) = 0.7 ⋅ 0.5 + 0.8 ⋅ 0.4 + 0.3 ⋅ 0.1 = 0.7
SS 2016
Prof. Dr. J. Schütze, FB GW
Im Beispiel
Wkt.1
17
Bayessche Formel
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
18
Bayessche Formel
Veränderte Fragestellung:
Ein Tor wurde erzielt.
Mit welcher Wahrscheinlichkeit kam
der Schuss von Stürmer B?
Satz (Bayessche Formel)
Ω = B1 ∪ B2 ∪ ... ∪ Bn , alle Bk seien paarweise disjunkt
Dann gilt
P ( Bi / A) =
Einschränkung der Grundgesamtheit
auf die Schüsse mit Torerfolg T (Kreis)
Ereignis ist nun ‚Schüsse von B , die zu
einem Tor führten‘ (gelbe Fläche).
P (T / B ) ⋅ P ( B )
P (T / A) ⋅ P ( A) + P (T / B ) ⋅ P ( B ) + P (T / R ) ⋅ P ( R )
0.8 ⋅ 0.4
0.8 ⋅ 0.4
P( B / T ) =
=
= 0.457
0.7 ⋅ 0.5 + 0.8 ⋅ 0.4 + 0.3 ⋅ 0.1
0.7
P( B / T ) =
Prof. Dr. J. Schütze, FB GW
P ( A / Bi ) ⋅ P ( Bi )
P ( A / Bi ) ⋅ P ( Bi )
= n
P ( A)
 P( A / Bi ) ⋅ P( Bi )
i =1
Die gesuchte Wahrscheinlichkeit P(B/T) ist der Anteil des gelben Segments an der
Fläche T.
SS 2016
P (T ) = 0.7 ⋅ 0.5 + 0.8 ⋅ 0.4 + 0.3 ⋅ 0.1 = 0.7
Wkt.1
19
Bedeutung des Satzes
Es erfolgt in gewissem Sinn die Umkehr von Ursache-Wirkungs-Beziehungen.
Man kennt die Wahrscheinlichkeit P(Wirkung / Ursache), mit der eine Ursache
eine bestimmte Wirkung nach sich zieht.
Oft fragt man dann bei Vorliegen einer Wirkung, mit welcher Wahrscheinlichkeit
eine bestimmte Ursache vorgelegen hat, d.h. man sucht P(Ursache / Wirkung).
So wird in der Medizin oft aufgrund einer Wirkung (Testergebnis, Befund) auf das
Vorhandensein einer Krankheit geschlossen.
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
20
Bayessche Formel
Bedingte Wahrscheinlichkeit und Diagnoseverfahren
Diagnostische Tests
Berechnung nach Bayes mit Pfaddiagramm
P (T / B ) ⋅ P ( B )
=
P (T )
P (T / B ) ⋅ P ( B )
P (T / A) ⋅ P ( A) + P (T / B ) ⋅ P ( B ) + P (T / R ) ⋅ P ( R )
Diagnostische Tests können i.a. Kranke und Gesunde nicht perfekt trennen.
Es liegt dann folgende Situation vor:
P( B / T ) =
Diagnose krank
DK
Diagnose gesund DG
krank K
gesund G
richtig positiv
falsch positiv
falsch negativ
richtig negativ
Die falsch negativen Fälle sind die nicht entdeckten Kranken.
Die falsch positiven Fälle sind die Gesunden, die der Test als krank einstuft.
Bedingte Wahrscheinlichkeiten liefern Kenngrößen zur Bewertung eines Tests,
Sensitivität, Spezifität (in Phase der Testkonstruktion)
positiv prädiktiver Wert, negativ prädiktiver Wert (in Phase der Anwendung)
P(B/T) erhält man, indem man das Verhältnis der Pfadwahrscheinlichkeit des
Pfades nach T über B zur Summe aller Pfadwahrscheinlichkeiten nach T
berechnet.
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
21
SS 2016
Prof. Dr. J. Schütze, FB GW
Bedingte Wahrscheinlichkeit und Diagnoseverfahren
Sensitivität und Spezifität
Entstehen eines Diagnoseverfahrens
Ereignisse und Wahrscheinlichkeiten
Ein bestimmter Parameter sei bei Erkrankten (im Mittel) deutlich erhöht.
Ziel: Festlegen eines Schwellwerts, bei Überschreitung Diagnose ‚Krank‘
Wie brauchbar ist das Verfahren?
G: gesund, K: krank, DK: Diagnose krank, DG: Diagnose gesund
Verteilung des Parameters in einer großen Gruppe Kranker und Gesunder:
Diagn. Gesund
Diagn. Krank
Fehldiagnosen
0.4
y 0.4
y
0.3
0.3
P(K)
P(DK/K)
P(DG/G)
Brauchbarkeit des Tests in Anwendungsphase (nach Bayes-Formel)
positiv prädiktiver Wert Anteil der Kranken unter ‚Diagnose krank‘
P(K/DK)
P ( K / DK ) =
Gesunde
0.0
0.0
15
15
16
16
17
17
18
18
Kranke
19
19
20
20
Schwellwert
21
21
Sensitivität ⋅ Prävalenz
Sensitivität ⋅ Prävalenz + (1 − Sensitivität) ⋅ (1 − Prävalenz)
negativ prädiktiver Wert Anteil der Gesunden unter ‚Diagnose gesund‘
22
22
P (G / DG ) =
xx
Falsch negative Falsch positive
22
Prävalenz Wahrscheinlichkeit für Auftreten der Krankheit
Sensitivität Anteil richtiger Diagnose unter den Kranken
Spezifität Anteil richtiger Diagnose unter den Gesunden
0.2
0.2
0.1
0.1
Wkt.1
P(G/DG)
Spezifität ⋅ (1 − Prävalenz)
Spezifität ⋅ (1 − Prävalenz) + (1 − Sensitivität) ⋅ Prävalenz
Anteile der Fehldiagnosen sind stark von Prävalenz abhängig!
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
23
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
24
Positive und negative Vorhersagewahrscheinlichkeit
Positive und negative Vorhersagewahrscheinlichkeit
Beispiel 5
0,03
Ω
0.97
0.03
0.97
0.99
DK
Kenngrößen in Anwendungsphase
0.01
DG
P(K/DK) für das Vorliegen der Krankheit,
wenn der Test positiv ist (PPV)
0.02
0.98
SS 2016
DK
G
DG
Wkt.1
25
Unabhängigkeit von Ereignissen
DK
DG
Zu berechnen sind (nach Bayes)
P(K/DK) bzw. P(G/DG)
P ( DK / K ) ⋅ P ( K )
P ( DK / K ) ⋅ P ( K ) + P ( DK / G ) ⋅ P (G )
0.99 ⋅ 0.03
=
= 0.60
0.99 ⋅ 0.03 + 0.02 ⋅ 0.97
d.h. nur 60% mit Diagnose Krank
sind auch wirklich krank,
40% der Fälle mit Diagnose Krank
sind Fehldiagnosen!
P ( DG / G ) ⋅ P (G )
P ( DG / G ) ⋅ P (G ) + P ( DG / K ) ⋅ P ( K )
0.97 ⋅ 0.98
=
= 0.999
0.97 ⋅ 0.98 + 0.01 ⋅ 0.03
d.h. 99.9% mit Diagnose Gesund
sind wirklich gesund,
0.1% der Kranken wird übersehen
SS 2016
Prof. Dr. J. Schütze, FB GW
3.5
Wkt.1
26
Wkt.1
28
A, B sind unabhängig, wenn
P ( A / B ) = P ( A / B ) = P ( A)
z.B. sind die Ereignisse
A: Proband hat Blinddarmentzündung
B: Proband hat Glaukom
vermutlich unabhängig.
Nach Definition der bedingten Wahrscheinlichkeit ist
P( A ∩ B)
, somit muss gelten P ( A) ⋅ P ( B ) = P ( A ∩ B )
P( A / B) =
P( B)
Definition
Der Begriff der Unabhängigkeit ist mathematisch fassbar über die bedingte
Wahrscheinlichkeit.
A, B sind stochastisch unabhängig, wenn gilt
P(A / B): Wahrscheinlichkeit, dass jemand Blinddarmentzündung bekommt, wenn er
ein Glaukom hat
P ( A ∩ B ) = P( A) ⋅ P( B)
Multiplikationssatz
P( A ∩ B) = P( A / B) ⋅ P( B)
P ( A ∩ B ) = P( A) ⋅ P( B), falls A, B unabhängig
P(A / B ): Wahrscheinlichkeit, dass jemand Blinddarmentzündung bekommt, wenn er
kein Glaukom hat
Prof. Dr. J. Schütze, FB GW
0.02
G
P(G) = 0.97, P(K) = 0.03
P(DK/K) = 0.99
P(DK/G) = 0.02
Unabhängigkeit von Ereignissen
Anschauliche Vorstellung über Unabhängigkeit der Ereignisse A, B:
Ereignis B hat keinen Einfluss darauf, ob Ereignis A eintritt oder nicht
SS 2016
DG
P (G / DG ) =
P(G/DG)für das Nichtvorliegen der Krankheit,
wenn der Test negativ ist (NPV)
Prof. Dr. J. Schütze, FB GW
0.01
P ( K / DK ) =
Wahrscheinlichkeiten im Pfaddiagramm
Ω
DK
0.98
P(G) = 0.97, P(K) = 0.03,
P(DK/K) = 0.99 (Sensitivität), folglich P(DG/K) = 0.01 (falsch negativ)
P(DK/G) = 0.02 (falsch positiv), folglich P(DG/G) = 0.98 (Spezifität)
K
0.99
K
Ein Diagnoseverfahren erkennt 99% der Erkrankten als krank, aber auch 2%
aller Gesunden werden als krank eingestuft.
Die Wahrscheinlichkeit für das Auftretens der Krankheit schätzt man in der
untersuchten Population mit 3%. Wie brauchbar ist das Verfahren?
Wkt.1
27
SS 2016
Prof. Dr. J. Schütze, FB GW
Rechnen mit Wahrscheinlichkeiten
Rechnen mit Wahrscheinlichkeiten
P ( A ∩ B ) , falls P(B)>0
P( B)
P ( A / B ) = P ( A)
P( A ∩ B) = P ( A / B) ⋅ P( B)
Beispiel 6
Ein idealer Würfel wird zweimal nacheinander gewürfelt.
Ereignis A: beim ersten Wurf fällt eine 6
Ereignis B: beim zweiten Wurf fällt eine 6
Sind A und B unabhängig?
Bedingte Wahrscheinlichkeit
Ergebnisraum bei zweimaligem Würfeln Ω = {(1,1),(1,2),...(1,6),(2,1),(2,1),...(2,6),...(6,6)}
Satz der totalen Wahrscheinlichkeit
Ω = B1 ∪ B2 ∪ ... ∪ Bn , paarweise disjunkt
P ( A) =  P ( A / Bk ) ⋅ P ( Bk )
somit
Bayessche Formel
Ω = B1 ∪ B2 ∪ ... ∪ Bn , paarweise disjunkt
P( Bi / A) =
Unabhängigkeit
Multiplikationssatz
P ( A ∩ B ) = P((6,6)) = 1 / 36
Andererseits ist
P( A / B) =
A = {(6,1),(6,2),...(6,6)}
P( A ∩ B) = P ( A) ⋅ P( B), falls A, B unabh.
n
k =1
P( A / Bi ) ⋅ P ( Bi )
n
 P( A / B ) ⋅ P( B )
k
k
k =1
B = {(1,6),(2,6),...(6,6)}
folglich ist
P ( A) = P ( B ) = 1/ 6
Wegen P ( A ∩ B ) = P ( A) ⋅ P( B ) sind die Ereignisse unabhängig.
SS 2016
Prof. Dr. J. Schütze, FB GW
3.6
Wkt.1
29
SS 2016
Prof. Dr. J. Schütze, FB GW
Wkt.1
30