17.12.2015 Röntgen- und Synchrotronstrahlung - Delta

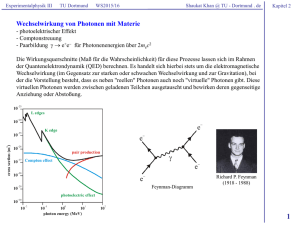
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
2.19 Emission, Absorption und Streuung von Röntgenstrahlung
1895 W. C. Röntgen entdeckt die "X-Strahlen"
1901 der erste Physik-Nobelpreis
1913 W. Coolidge entwickelt die Röntgenröhre
1912 Röntgenbeugung an Kristallen durch
M. v. Laue, W. H. Bragg, W. L. Bragg u.a.
Wilhelm Conrad Röntgen
(1845-1923)
Ein Elektronenstrahl wird elektrostatisch auf einige 10 keV
beschleunigt und trifft auf eine Anode aus einem schweren
Material (Kupfer, Wolfram). Dadurch entstehen zwei Arten
von kurzwelliger Strahlung:
- Bremsstrahlung aufgrund der Abbremsung
(jede Beschleunigung einer Ladung bewirkt
elektromagnetische Strahlung, vgl. Elektrodynamik.
- charakteristische Röntgenstrahlung aufgrund von
Übergängen zwischen inneren Schalen der Anodenatome.
William Lawrence Bragg
(1890-1971)
William Henry Bragg
(1862-1942)
Kurzwelliges Ende der Bremsstrahlung: Elektronenenergie = Photonenenergie
e  U  h   h
c
min

min 
hc
e U
Max von Laue
(1879-1960)
1
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Form des Bremsstrahlspektrums
I

1 

 1
2 
  min 
Charakteristische Röntgenlinien
Übergänge im Bohrschen Atommodell
idealisiert für H-ähnliche Atome
realistisch für schwerere Atome
(S: Abschirmfaktor)
Linienspektrum
"Schalen"
n 1
n2
n3
n4

K
L
M
N
 1
1 
E  R  Z 2   2  2 
 n1 n2 
1
2  1
E  R  Z  S    2  2
 n1 n2
nach
von
n1  1
n2  2
K
n1  1
n2  3
Kß

n1  2
n2  3
L
n1  2
n2  4
Lß
n1  3
n2  4
M
n1  3
n2  5
M



Frequenz
Energie
Wellenlänge
Bezeichnung

Bragg-Bedingung
n    2d  sin 
d: Abstand der Gitterebenen
n: Beugungsordnung
2
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Absorption von Röntgenstrahlung
Die Wechselwirkung von Photonen mit Materie ist für viele Bereich
der Physik von Interesse. Im Röntgenbereich gibt es folgende Effekte,
die eine Absorption von Photonen bewirken:
- Photoeffekt: das Photon wird absorbiert, ein Elektron wird emittiert.
Das Atom kehrt über Fluoreszenz oder Emission von Auger-Elektronen
in den Grundzustand zurück.
- Compton-Streuung: das Photon streut an einem (fast freien) Elektron
der äußeren Atomhülle und verliert einen Teil seiner Energie.
Das Elektron wird dabei emittiert.
- Rayleigh-Streuung: bei nicht allzu hoher Photonenenergie (einige 10 keV)
streut das Photon am gesamten Atom, ohne Energie zu verlieren.
- Paarbildung: oberhalb einer Photonenenergie von 1,055 MeV (2 x me)
entsteht in der Umgebung eines Atoms ein Elektron-Positron-Paar.
Bei sehr hohen Photonenenergien (Gamma-Strahlung) erzeugen die Teilchen
Bremsstrahlung, die weitere e+e-Paare erzeugen (elektromagnetischer Schauer).
Absorptionskoeffizient
Die einfallende Strahlungsleistung wird durch Streuung und Absorption nach einer Schichtdicke x verringert
dP    P  dx

P( x)  P(0)  e x
(    s  a )
(Streuung + Absorption)
a  n   a
a
  ka  


P( x)  P(0)  e k a  x
Absorptionskoeffizient = Anzahldichte · Absorptionsquerschnitt
 a   1
m
n  13
m
m3
    m 2
m
ka: Massenabsorptionskoeffizient
ka 
a
n  a
a


 n  mAtom mAtom
m3
m2
k a  

m  kg kg
3
Experimentalphysik III
TU Dortmund
Differenzieller und
totaler Wirkungsquerschnitt
 tot 
d
4 d  d
WS2015/16
N
Shaukat Khan @ TU - Dortmund . de

1
s
n
1
m 2s

nS  V

1
 m3
3
m
d
 
d
m2
sr

Kapitel 2

sr
Teilchen/s in  = Flussdichte × Zahl der Streuzentren × diff. Wirkungsquerschnitt × Raumwinkel
Photoeffekt
Kinetische Energie des emittierten Elektrons = Photonenenergie  Austrittsarbeit
Ekin  h   Wa
Ek ist das Energieniveau des Elektrons vor der Emission, Eion ist die Energie des ionisierten Atoms
Absorptionsquerschnitt (empirisch):
 a  Z 4  3
Zusätzlich treten aber bei bestimmten Wellenlängen Sprünge auf. Wenn man die Wellenlänge kontinuierlich
verkleinert, steigt bei den sogenannten Absorptionskanten der Absorptionsquerschnitt sprunghaft an. Dies
ist immer dann der Fall, wenn die Photonenenergie für einen weiteren Übergang eines Elektrons in eine
höhere Schale ausreicht, d.h. die Wellenlängen der Absorptionskanten entsprechen denen der
charakteristischen Röntgenlinien.
Moseleysches Gesetz
 1 1
2
h   R  Z eff
  2  2 
 n1 n2 
R = Rydberg-Konstante in Energie-Einheiten
mit Korrektur der reduzierten Masse
Zeff = Z – S = um die Abschirmwirkung
korrigierte Kernladungszahl
Historisch wurde dieses Gesetz verwendet um die damals
unbekannte Kernladung einiger Elemente zu bestimmen.
Die Absorptionskanten sind nach den Hauptquantenzahlen der
beteiligten Elektronen benannt (K-Kante, L-Kante usw.), die
z.T. deutlich in eine Feinstruktur aufspalten (z.B. LI, LII LIII).
Henry Moseley
1887 -1915
4
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Compton-Effekt
Photon-Elektron-Streuung.
Klein-Nishina-Theorie im Rahmen der Quantenelektrodynamik.
Grenzfall für kleine Photonenenergie: Thomson-Streuung
d 1 2
 re 1  cos 2 
d 2
8
 T    re2  6,652 10 29 m 2
3

     2c  sin 2


2
mit
differenzieller und totaler
Thomson-Wirkungsquerschnitt
mit
c 
Joseph J. Thomson
(1856 - 1940)
e2
re 
 2,818 10 15 m
2
4   0  me c
h
m0  c
Arthur Compton
(1892 - 1962)
(klassischer Elektronenradius)
Compton-Streuformel
Paarbildung
Wirkungsquerschnitt steigt über 1,022 MeV stark an,
Berechnung aufwändig, hängt von Abschirmungseffekten
innerhalb des Atoms ab.
(Wikipedia, Dscraggs)
5
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Anwendung von Röntgenstrahlung
Spektroskopie
EXAFS - extended X-ray absorption fine structure
NEXAFS - near-edge x-ray absorption spectroscopy
Die Streuung der Materiewelle des beim Photoeffekt auslaufenden
Elektrons an den umliegenden Atomen bewirkt eine Feinstruktur der
Absorptionskante, deren Analyse Aufschluss über die Lage der Atome
zueinander gibt.
Abbildung
Photonen:
einfacher Schattenwurf, Phasenkontrast, Holografie
Abbildung mit Spiegeln (unter streifendem Einfall),
Linsen (Luft in Be, Brechungsindex < 1) oder Zonenplatten
Elektronen:
fokussierte Photoelektronen (Linsen wir im Elektronenmikroskop)
Diffraktion (Beugung)
z.B. Proteinkristallografie
6
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
2.20 Quellen für Vakuum-Ultraviolett- und Röntgenstrahlung
- Röntgenröhre (seit 1913)
- Synchrotronstrahlungsquellen (seit ~1970)
- Hohe Laser-Harmonische (seit ~1990)
- Freie-Elektronen-Laser (seit 2000)
Brillanz = Photonenzahl
pro Zeit (s)
pro Quellgröße (mm2)
pro Raumwinkel (mrad2)
pro Energieintervall (0,1%bw)
Spitzenbrillanz = Brillanz im zeitlichen
Maximum eines Strahlungspulses
Fortschritte:
- Röntgenröhre mit Glühkathode
- Röntgenröhre mit rotierender Anode
- Synchrotronstrahlungsquellen
- Wiggler und Undulatoren
- Freie-Elektronen-Laser
Synchrotronstrahlung
Abstrahlung elektromagnetischer Wellen durch relativistische Elektronen aufgrund einer Kreisbeschleunigung.
Hohe Intensität durch starke relativistische Verschiebung des Strahlungskegels in Vorwärtsrichtung.
7
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Beschleunigung von Elektronen auf relativistische Energien (typisch GeV)
Beschleunigung durch elektrische Feld einer Hochfrequenzwelle (GHz)
- Elektronenerzeugung mit elektrostatischer Vorbeschleunigung
- weitere Vorbeschleunigung meist in einem Linearbeschleuniger
(Röhre mit Irisblenden, um die Phasengeschwindigkeit der HF-Welle
auf die Elektronengeschwindigkeit (≈ c) zu verlangsamen.
- Beschleunigung auf GeV-Energien meist in einem Synchrotron
(ringförmige Magnetanordnung mit HF-Resonatoren, wobei die
Magnetfelder synchron mit dem Energiezuwachs ansteigen, damit die
Elektronen auf derselben Bahn bleiben)
- anschließend Injektion in einen Speicherring (ringförmige Maschine
ähnlich einem Synchrotron, wobei die Elektronenenergie konstant bleibt
und HF-Resonatoren nur die Synchrotronstrahlungsverluste kompensieren.
Erste Beobachtung von Synchrotronstrahlung 1947 in einem
Elektronensynchrotron bei General Electric in Schenectady/NY
- daher der Name. Praktisch nutzbare Synchrotronstrahlung wird
aber nicht in Synchrotrons, sondern in Speicherringen erzeugt.
Eigenschaften der Strahlung
Mittlerer Energieverlust eines Elektrons pro Umlauf
(360 Grad mit konstantem Biegeradius R)

E 4 GeV 4
EkeV   88,5
Rm

8
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Eigenschaften von Synchrotronstrahlung
Welche Eigenschaften von Interesse sind, hängt von der Anwendung ab z.B.
- Intensität (Leistung, Pulsenergie, Photonenzahl etc)
- Winkelverteilung
- spektrale Verteilung
- weitere Eigenschaften wie Pulsdauer, Polarisation, etc.
a) Strahlung aus Dipolmagneten
Energieverlust eines Elektrons der Energie E bei einem Umlauf mit konstantem Biegewinkel R

E 4 GeV 4
E1 keV   88,5
Rm

Leistung bei gegebenem Strahlstrom I:
P  ne
E1 I  T E1
E

I 1
T
e T
e

PW  E1 eV   I A
Winkelverteilung
- horizontal: ein Fächer, dessen Winkel dem Biegewinkel des Magneten entspricht (typisch 5–20 Grad)
- vertikal: typischer Wert der Standardabweichung
2
(hängt im Detail von der Wellenlänge ab)   1  me  c


Spektrale Verteilung: breites Spektrum
(weil kein periodischer Vorgang) mit Maximum im keV-Bereich.
Die sog. "kritische Energie", die das Spektrum
E3
in zwei gleich große Leistungsbeiträge teilt, ist
E 
krit
R
E
9
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
b) Strahlung aus Wigglern und Undulatoren
Wiggler und Undulatoren sind Anordnungen von abwechselnd gepolten
Dipolmagneten, in denen die Elektronen eine sinusförmige Bahn verfolgen.
Der Abstand zwischen zwei gleichartigen Dipolen heißt Undulatorperiode.
Der Unterschied zwischen Wiggler und Undulator ist etwas unscharf:
Ein typischer Wiggler hat ein hohes Magnetfeld, so dass die Strahlung der
aufeinanderfolgende Bögen wenig überlappt. Damit unterscheidet sich ein
Wiggler von Dioplmagneten nur in der Intensität ~ Zahl der Bögen.
Ein typischer Undulator hat ein niedriges Magnetfeld, so dass sich die Strahlung der flachen Bögen stark überlappt.
Das elektrische Feld am Ort des Beobachters ist periodisch . Dadurch entsteht ein Linienspektrum mit der
Grundwellenlänge
2

U  K
1 
2
2 2 



mit
K  93,4  U m  B0 T
 
1
NU
und ungeradzahligen Harmonischen /3, /5 usw. auf der Undulatorachse. Bei Beobachtungswinkeln ≠ 0 werden
auch die geradzahligen Harmonischen sichtbar und alle Linien sind rotverschoben. Die Linienbreite mit mit der
Zahl der Undulatorperioden NU ab
Leistung von Wigglern/Undulatoren bei gegebenem Strahlstrom I:


PW  7.26  E 2 GeV 2  I A K 2  NU / cm
Winkelverteilung von Strahlung aus Undulatoren
- horizontal und vertikal
 
1
NU 

Brillanz  N 2
10
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Bauformen von Wigglern und Undulatoren
Permanentmagnete
- Magnetfeld an der Oberfläche bis ca. 1,6 T, gekühlt auch höher)
- oft Hybridbauweise: Eisenpole mit Permanentmagneten dazwischen
- Magnetfeld auf der Strahlachse wird durch mechanische Abstandsänderung eingestellt
Elektromagnete
- Spulen mit Eisenjoch (an der Oberfläche bis ca. 1,8 T)
- supraleitende Magnete (bis 10 T)
Typische spektrale Verteilungen der Synchrotronstrahlung auf einer doppelt-logarithmischen Skala:
Dipolmagnete (bend), supraleitende Dipole (WLS),
Wiggler (W125) sowie die erste, dritte und fünfte
Harmonische von Undulatoren (U41 etc).
11
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Typische Synchrotronstrahlungquelle
- Elektronenquelle, Vorbeschleuniger (Linearbeschleuniger), Hauptbeschleuniger (Synchrotron), Speicherring;
Strahlenenergie: einige 100 MeV bis 8 GeV (SPring8/Japan); Strahlstrom: einige 100 mA
- Speicherring: Umfang 10 m (Helios 2, Singapur) bis 2,3 km (PETRA III, Hamburg);
Vakuumkammer: Edelstahl, Aluminium oder Kupfer; Ultrahochvakuum
Magnete: Dipole (Kurve), Quadrupole (Fokussierung), Sextupole (Fokussierung), kleine Dipole (Bahnkorrektur)
Hochfrequenz-Resonatoren: einige 10 bis 100 kW
Wiggler und Undulatoren: Permanentmagnete oder Elektromagnete (normal- oder supraleitend)
- Strahlauslassrohre ("beamlines") mit gekrümmten Spiegeln und Gitter- oder Kristall-Monochromatoren
BESSY in Berlin-Adlershof
12
Experimentalphysik III
TU Dortmund
WS2015/16
Shaukat Khan @ TU - Dortmund . de
Kapitel 2
Freie-Elektronen-Laser (FEL)
Neuartige Röntgenquelle mit extremer Spitzenbrillanz, bestehend aus Linearbeschleuniger und langem Undulator
- Prinzip in den 1970er Jahren publiziert (John Madey, SLAC)
- erste FELs im Infrarotbereich
- FELs für kurze Wellenlängen: FLASH in Hamburg, FERMI@Elettra in Trieste/Italien
- erster Röntgen-FEL 2009 LCLS in Menlo Park/USA, 2010 SACLA in Hyogo/Japan
- weitere FELs in Bau, z.B. Europ. XFEL in Hamburg, SwissFEL in Villigen/Schweiz, PAL-FEL in Pohang/Korea
- sehr kurze Elektronenpakete, kleiner Strahlquerschnitt  hohe Elektronendichte ermöglicht FEL-Prozess
- FEL-Prozess verstärkt Licht und erzeugt kohärente Strahlung (extrem hohe Intensität ~ Elektronenzahl 2):
elektrisches Feld der Strahlung bewirkt in einem Undulator eine periodische Anordnung der Elektronen
("microbunching"), die zur kohärenten Abstrahlung führt
FEL nach dem SASE-Prinzip (self-amplified spontaneous emission), bei dem kein extern zugeführter Lichtpuls vom FEL
verstärkt wird, sondern die Strahlung im ersten Teil des langen Undulators als Synchrotronstrahlung entsteht und auf die
Elektronen zurückwirkt, so dass sich diese im Abstend der Wellenlänge anordnen und kohärent strahlen.
numerische Simulation des MicrobunchingProzesses. Der Abstand zwischen den Maxima
der Elektronendichte beträgt eine Wellenlänge
der FEL-Strahlung
13