3. Vektoren - ITP, TU Berlin

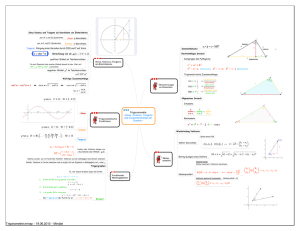
3. Vektoren
3.1
Definition, Einheitsvektoren, Komponenten, Rechenregeln, Vektorraum
Neben skalaren (Zahlen mit Maßeinheit wie Masse, Energie, Druck usw.) werden in der
Physik vektorielle Größen ("Pfeile" mit Richtung und Länge) verwendet: Ortsvektor,
Geschwindigkeit, Verschiebung, Kraft, Feldstärke usw.
† Bahnkurve einer Kanonenkugel mit Ortsvektor, Momentangeschwindigkeit und
Schwerkraft (Skizze V)
† Verschiebungsvektor: r1 + r12 = r 2 (Skizze V)
Grafisch werden Vektoren durch frei verschiebbare Pfeile "von A nach B" veranschaulicht,
Vektoren sind also Größen, die Betrag und Richtung besitzen.
Vereinbarung zur Schreibweise: Vektoren unterstrichen, a, Betrag (Länge) des Vektors a ohne
Unterstrich, a = a .
Im dreidimensionalen Raum sind drei Zahlen (Betrag und zwei Winkel → sphärische
Koordinaten r bzw. ϕ und q; Skizze V) zur eindeutigen Bestimmung eines Vektors
ausreichend. Im kartesischen Koordinatensystem werden die senkrechten Projektionen auf die
Koordinatenachsen verwendet (Komponenten des Vektors):
x = r cos ϕ sin θ,
y = r sin ϕ sin θ,
z = r cos θ.
Definition: Vektoren im dreidimensionalen Raum sind geordnete Zahlentripel, die sich auf
ein Koordinatensystem beziehen
⎛x⎞
⎛ a1 ⎞
⎜ ⎟
⎜ ⎟
r = ⎜ y ⎟ , a = ⎜ a 2 ⎟ usw.
⎜z⎟
⎜a ⎟
⎝ ⎠
⎝ 3⎠
1
Bem.: geordnete Zahlentripel
Zahlentripel sind genau dann Vektoren, wenn sie sich bei Drehung des Koordinatensystems
gemäß a ' = D a transformieren ( D - Drehmatrix, vergleiche 4. Vorlesung).
Ein Zahlentripel aus Temperatur, Druck und Volumen eines Gases bildet beispielsweise
keinen Vektor.
In der linearen Algebra werden Vektoren ohne Bezug auf ein Koordinatensystem ad hoc als
(geordnetes) n-Tupel von Zahlen definiert, für die bestimmte Rechenregeln gelten.
Definition:
⎛ a1 ⎞
⎜ ⎟
a =⎜ M ⎟=
⎜a ⎟
⎝ n⎠
n
∑a e ∈ℜ
i
i
n
oder C n , d.h., die Zahlen ai sind reell oder komplex.
i =1
Die Vektoren werden als Elemente eines, zunächst endlichdimensionalen, Vektorraums
aufgefasst (vgl. Vorlesung Lineare Algebra).
• Komponentendarstellung von Vektoren
a = a1 e1 + a 2 e 2 + a 3 e3 Komponentendarstellung von a bzgl. e1, e2, und e3.
Für Vektoren sind die Addition und die Multiplikation mit einer Zahl definiert: Vektoren
werden addiert ("Kräfteparallelogramm, Addition ist kommutativ) und mit Zahlen
multipliziert, indem man ihre Komponenten addiert bzw. mit Zahlen multipliziert.
• Einheitsvektoren (EHV) sind Vektoren vom Betrag (der Länge) 1: Für einen beliebigen
Vektor a mit Betrag a ist
e=
1
a
a
der Einheitsvektor in Richtung von a. Einheitsvektoren sind besonders gut zur Kennzeichnung
von Richtungen geeignet. Im dreidimensionalen Raum lassen sich Koordinatensysteme
bequem durch drei Einheitsvektoren
2
⎛ 1⎞
⎛ 0⎞
⎛ 0⎞
⎜ ⎟
⎜ ⎟
⎜ ⎟
e x = e1 = ⎜ 0 ⎟ , e y = e 2 = ⎜ 1 ⎟ bzw. e z = e3 = ⎜ 0 ⎟
⎜ 0⎟
⎜ 0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
festlegen (Rechtssystem, Dreibein, Skizze V).
Aus der Vorlesung lineare Algebra die Begriffe lineare Unabhängigkeit von Vektoren, Basis
und die Axiome des linearen Vektorraums wiederholen.
3.2
Produkte von Vektoren
Es gibt zwei physikalisch sinnvolle Möglichkeiten für einfache Vektorprodukte: das
sogenannte innere und das äußere Produkt zweier Vektoren.
3.2.1 Skalarprodukt (inneres Produkt)
- Physikalische Motivation: Die bei Verschiebung eines Körpers K um Δr durch eine durch
eine in seinem Schwerpunkt angreifende Kraft F verrichtete Arbeit ist proportional zu
⎧ F cos ϕ
ΔA ~ ⎨
⎩ Δr
(Kraft F zieht Körper K in Richtung Δr , ϕ ist der Winkel zwischen den beiden Vektoren F
und Δr , F cos ϕ ist also die senkrechte Projektion des Vektors F auf den Vektor Δr , Skizze
V) . Wir definieren
ΔA = F Δr cos ϕ =: F ⋅ Δr , für infinitesimal kleine Verschiebung dr schreiben wir dA = F ⋅ dr .
Allgemein ist das Skalarprodukt aus den Vektoren a und b die Zahl
n
a ⋅ b := a b|| = a || b = a b cos (eingeschlossenen Winkels) = ∑ a i bi , es gilt
i =1
b
a
= .
b|| a ||
3
• Skalarprodukt in Komponentenschreibweise, Summenkonvention
Mit Hilfe der senkrecht aufeinander stehenden EHV in x, y und z-Richtung (kartesisches
Koordinatensystem)
⎛ 1⎞
⎛ 0⎞
⎛ 0⎞
⎜ ⎟
⎜ ⎟
⎜ ⎟
e x = e1 = ⎜ 0 ⎟ , e y = e 2 = ⎜ 1 ⎟ bzw. e z = e3 = ⎜ 0 ⎟
⎜ 0⎟
⎜ 0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
haben wir
a = a1 e1 + a 2 e 2 + a 3 e3 ,
also
3
⎧0, i ≠ j
a ⋅ b = ( a1 e1 + a 2 e 2 + a 3 e3 ) ⋅ ( b1 e1 + b 2 e 2 + b 3 e3 ) = ... ei ⋅ e j = ⎨
... = a1b1 + a 2 b 2 + a 3b3 = ∑ a i bi
i =1
⎩1, i = j
Summenkonvention
Zur Vereinfachung der Schreibweise hat Einstein vorgeschlagen, über doppelt vorkommende
Indices von 1 …. n zu summieren, ohne das Summenzeichen anzugeben:
3
a ⋅ b = ∑ a i bi = a i bi .
i =1
Bequem ist auch die Einführung des Kronecker-Symbols
⎧ 0, i ≠ j
δij := ei ⋅ e j = ⎨
.
1
,
i
=
j
⎩
Dann haben wir statt der ganzen Schreiberei oben einfach
a ⋅ b = a i ei ⋅ b k e k = a i b k ei ⋅ e k = a i b k δik = a i b i .
4
†
Überzeugen Sie sich von der Richtigkeit der Relationen
δii = δ nn = 3 , δij δ jk = δik , c k a i a j b k δij = a 2 (c ⋅ b) .
• Weitere ausgewählte Eigenschaften des Skalarprodukts
- a ⋅ b = b ⋅ a , speziell gilt e ⋅ e = 1 für alle EHV.
- Betrag, Norm, Länge des Vektors a : a ≡ a := a ⋅ a
im R 3
=
a12 + a 22 + a 32
- Orthogonalität: Zwei Vektoren a und b heißen orthogonal, wenn a ⋅ b = 0 .
3.2.2 Vektorprodukt (Kreuzprodukt, äußeres Produkt)
- Physikalische Motivation: Geladenes Teilchen im Magnetfeld
Aus dem Experiment ergibt sich, das die auf das Teilchen
wirkende → Lorentz-Kraft FL betragsmäßig proportional zu
q
⎧
FL ~ ⎨
⎩ v B⊥ = v ⊥ B
(Skizze aus V)
und senkrecht zu beiden Vektoren v und B gerichtet ist (senkrecht auf der von v und B
aufgespannten Ebene steht; rechte Handregel üben). Dabei bezeichnen q die Ladung, v die
Geschwindigkeit des Teilchens, B die magnetische Induktion und ⊥ die Komponenten der
Vektoren senkrecht zum jeweiligen Partner.
5
†
Weitere Beispiele:
Drehmoment M = r × F , Drehimpuls L = r × p .
- Allgemeine Definition des Vektorprodukts aus zwei Vektoren a und b:
a × b = a b sin( des eingeschlossenen Winkels) e .
(Skizze aus V)
Hier ist e der senkrecht auf a und b stehende EHV (Rechtssystem, rechte Hand Regel). Der
Betrag des Vektorprodukts ist gleich der Fläche des durch a und b definierten
Parallelogramms
a × b = a b sin ϕ
(zeigen).
• Vektorprodukt in Komponentendarstellung
EINSCHUB: 4. Matrizen und Determinanden
Eine Matrix A ist ein Schema von m × n Zahlen aij bestehend aus i = 1, 2, ... , n Zeilen und
j = 1, 2, ... , m Spalten
⎛ a11 a12 L a1n ⎞
⎜
⎟
⎜ a 21 a 22 L a 2 n ⎟
.
A = (a ij ) = ⎜
M
M
M
M ⎟
⎜
⎟
⎜a
⎟
⎝ m1 a m 2 L a mn ⎠
(Matrix "vom Typ m × n")
Im Folgenden seien die Matrixelemente aij reelle Zahlen sowie m und n endlich.
6
4.1
Rechenregeln
Gleichheit von zwei Matrizen: A = B , wenn aij = bij für alle i, j.
Summe zweier Matrizen gleichen Typs: C = A + B mit cij = aij + bij für alle i, j,
wobei A + B = B + A → Addition von Matrizen kommutativ.
Multiplikation einer Matrix mit einer Zahl: α A = (α a ij ) (alle Elemente mit α multiplizieren).
T
T
Die zu A transponierte Matrix A mit a ij = a ji entsteht durch Vertauschung der Zeilen und
Spalten von A .
Offensichtlich können Vektoren als Matrizen aufgefasst werden, z.B. im R3
⎛ a1 ⎞
⎜ ⎟
T
Spaltenvektor a = ⎜ a 2 ⎟ Zeilenvektor a = (a1 , a 2 , a 3 )
⎜a ⎟
⎝ 3⎠
4.2
Multiplikation von Matrizen
Sei A = (a ij ) eine Matrix vom Typ mA × nA und B = (b ij ) eine Matrix vom Typ mB × nB .
Nur wenn A genauso viele Spalten wie B Zeilen hat (nA = mB), ist das Produkt beider
Matrizen definiert, wobei gilt
C = A × B = (c ij ) , c ij = a ik b kj Summenkonvention!
Also werden paarweise die Elemente der i-ten Zeile von A mit den Elementen der k-ten Spalte
von B multipliziert und addiert. M.a.W.: Das Matrixelement cij ist das Skalarprodukt aus dem
i-ten Zeilenvektor von A und dem j-ten Spaltenvektor von B . Die Produktmatrix hat mA
Zeilen und nB Spalten.
7
Im Gegensatz zur Addition ist die Multiplikation von Matrizen i.a. nicht kommutativ!
⎛ 3 6⎞
⎛ 3⎞
⎛ 3⎞
⎟⎟
A = (1 2), B = ⎜⎜ ⎟⎟ , A ⋅ B = (3 + 8) = (11) , B ⋅ A = ⎜⎜ ⎟⎟ ⋅ ( 1 2 ) = ⎜⎜
1×1−Matrix
⎝ 4 8⎠
⎝ 4⎠
⎝ 4⎠
■
2×2−Matrix
Für nichtquadratische Matrizen verhindert oft schon die Bedingung n A ≠ n B die
Vertauschbarkeit. Dennoch kommutieren auch quadratische Matrizen i.a. nicht.
⎛1 2⎞
⎛ 5 6⎞
⎟⎟ , B = ⎜⎜
⎟⎟
A = ⎜⎜
⎝ 3 4⎠
⎝ 7 8⎠
■
⎛ 5 + 18 10 + 24 ⎞ ⎛ 23 34 ⎞
⎛ 5 + 14 6 + 16 ⎞ ⎛ 19 22 ⎞
⎟⎟
⎟⎟ = ⎜⎜
⎟⎟ , B ⋅ A = ⎜⎜
⎟⎟ = ⎜⎜
A ⋅ B = ⎜⎜
⎝ 7 + 24 14 + 32 ⎠ ⎝ 31 46 ⎠
⎝15 + 28 18 + 32 ⎠ ⎝ 43 50 ⎠
Da multiplikativ vertauschbare Matrizen etwas Besonderes sind, definiert man:
Def.: Die Matrizen A und B heißen vertauschbar (kommutieren), wenn
[A, B] := A ⋅ B − B ⋅ A = 0
gilt.
2
n
- Potenzen A ,..., A können nur für quadratische Matrizen A gebildet werden. Dabei gilt
∞
A := A ⋅ A = (a ik a kj ) , e := ∑
2
A
n =0
1 n
d At
At
A usw. (Beachte: e = Ae )
dt
n!
Das Skalarprodukt zweier Vektoren lässt sich als Matrixmultiplikation darstellen, z.B.
T
T
a = (a 1 , a 2 , a 3 ) = A , b = (b1 , b 2 , b 3 ) = B , a ⋅ b = a i b i = A ⋅ B = A ⋅ B .
8
4.3
Determinante einer quadratischen n × n - Matrix
Determinante der quadratischen Matrix A ist die Zahl
Def.: Det ( A ) ≡ A =
a11
a12
a 21
a 22 L a 2 n
M
L a1n
M
M
M
:= a11 A11 − a12 A12 + a13 A13 − / + ... a1n A1n
a n1 a n 2 L a nn
mit den Unterdeterminanten Aik . Aik ist die Determinante n-1 ten Grades, die aus der
Determinante von A durch Streichung ihrer i-ten Zeile und ihrer k-ten Spalte entsteht. Diese
rekursive Definition führt die eine Determinante n-ten Grades auf eine Summe von
Determinanten n-1 -ten Grades zurückführt. Falls n = 1, ist die Determinante das
Matrixelement selbst.
■
Nach dieser Definition berechnet sich z.B. die Determinante einer quadratischen
Matrix 3-ten Grades wie folgt
a 11
a 12
a 13
a 21
a 22
a 23 = a 11
a 31
a 32
a 33
a 22
a 23
a 32
a 33
− a 12
a 21 a 23
a 31
a 33
+ a 13
a 21
a 22
a 31
a 32
=
= a 11 (a 22 a 33 − a 23a 32 ) − a 12 (a 21a 33 − a 23a 31 ) + a 13 (a 21a 32 − a 22 a 31 ) .
Für derartige Determinanten 3. Ordnung (und nur für diese!) ist die häufig verwendete
Sarrus´sche Regel gültig:
a 11 a 12
a 21 a 22
a 31 a 32
a 13
a 23
a 33
a 11 a 12
a 21 a 22
a 31 a 32
Terme mit positivem (negativem) Vorzeichen entstehen aus dem wie oben erweiterten
Schema durch Produktbildung entlang und parallel zur Haupt- (Neben-) Diagonalen
(durchgezogene bzw. unterbrochene Linien), man verifiziert leicht das obige Ergebnis.
9
ZURÜCK ZU KAPITEL 3:
• Vektorprodukt in Komponentendarstellung
Das Vektorprodukt von a , b œ R3 ist der Vektor (Komponentendarstellung)
e1
e2
e3
c = a × b = a1
b1
a2
b2
a3 =
b3
= e1
a2
b2
a
a3
− e2 1
b1
b3
a
a3
+ e3 1
b1
b3
a2
= e1 (a 2 b 3 − a 3b 2 ) − e 2 (a1b 3 − a 3b1 ) + e3 (a1b 2 − a 2 b1 )
b2
Beachte, dass a × b ⊥ a , b und a × b = − b × a gilt.
Zur weiteren Vereinfachung der Schreibweise können wir das ε- oder Levi-Civita-Symbol
verwenden
⎧ + 1, wenn i, j, k zyklisch zu 1,2,3 (123, 231, 312)
⎪
ε ijk := ei ⋅ (e j × e k ) = ⎨− 1, wenn i, j, k antizyklisch zu 1,2,3 (213, 132, 321) .
⎪ 0, ansonsten (z.B. mindesten zwei gleiche Indices)
⎩
Man findet dann
3
c = a × b = ∑ ε ijk a i b j e k = ε ijk a i b j e k oder ci = (a × b)i = ε ijk a j b k
i , j,k
10