Probeklausur (14.7.2010) - qoqi.physik.uni
Werbung

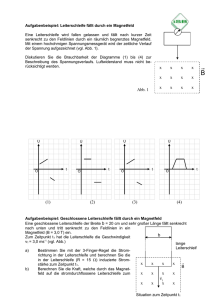
Experimentalphysik für Naturwissenschaftler 2 Universität Erlangen–Nürnberg SS 2010 Probeklausur (14.7.2010) Aufgabe 1: Wetterballon (8 Punkte) In einem Wetterballon werden 10 m3 Helium bei einer Umgebungstemperatur von 15◦ C gefüllt. Beim Aufsteigen dehnt sich das Volumen aus. Bei einer bestimmten Höhe hat er das Doppelte seines Ausgangsvolumen erreicht und platzt. Berechnen Sie die Höhe h, bei der der Ballon platzt. Die atomare Masse von Helium beträgt mHe = 6, 64 · 10−24 g. Hinweis: Sie Helium als ein ideales Gas und verwenden Sie die barometrische Höhenformel: p(h) = Betrachten mgh p0 ·exp − kB T ; nehmen Sie an, dass die Temperatur unabhängig von der Höhe h konstant ist; kB = 1, 38·10−23 J/K. Lösung: p 1 V1 = p21 V2 gh Barometrische Höhenformel: p2 = p1 · exp − mHe = kT 1 kT → h = − mHe g · ln 2 → h = 42325m Ideale Gasgleichung: p 1 V1 T1 = p 2 V2 T2 → p2 = p1 2 → 1 2 gh = exp − mHe → ln kT 1 2 gh = − mHe kT Aufgabe 2: Zustandsänderungen (8 Punkte) Skizzieren Sie in einem p-V-Diagramm qualitativ den Verlauf für folgende reversible Zustandsänderungen: a) isotherm, b) isobar, c) isochor, und d) adiabatisch. Berechnen Sie für alle vier Fälle jeweils ∆U , ∆Q und ∆W . Lösung: a) Isotherme im pV-Diagramm ∆U = n · RCV ∆T = 0 RV V VA ∆W = − VAE P dV = −nRT VAE dV V = n · R · T ln( VE ) 1. HS: ∆U = ∆Q + ∆W → ∆Q = −∆W b) Isobare ist horizontale Gerade im p-V-Diagramm. ∆W = −P ∆V = −P (V2 − V1 ) = −n · R · ∆T = −n · R · (T2 − T1 ) ∆U = n · CV · ∆T = n · CV · (T2 − T1 ) ∆Q = ∆U − ∆W = n · CV · (T2 − T1 ) + n · R · (T2 − T1 ) = (CV + R) · n · (T2 − T1 ) = CP · n · (T2 − T1 ) 1 c) Isochore ist eine vertikale Gerade im p-V-Diagramm. ∆W = 0 ∆U = n · CV · ∆T = n · CV · (T2 − T1 ) ∆Q = ∆U d) Adiabate im pV-Diagramm ∆Q = 0 ∆U = n · CV · ∆T = n · CV · (T2 − T1 ) ∆W = ∆U Aufgabe 3: Ideales Gas und Maxwell-Boltzmann-Verteilung (8 Punkte) a) Durch was zeichnet sich ein ideales Gas aus? Nennen Sie mindestens drei Annahmen. b) Was beschreibt die Maxwell-Boltzmann-Verteilung? Wie sieht ihr charakteristischer Verlauf aus und wie ändert sich dieser, wenn die Temperatur des Gases geändert wird? Lösung: a) • (ausdehnungslose) Massenpunkte • identische Teilchen • keine Fernwechselwirkung zwischen den Teilchen • Wechselwirkung nur durch elastische Stöße, entweder mit der Wand oder untereinander • Bewegung ist statistisch verteilt, so dass Gesamtimpuls Null ist b) Die Maxwell-Boltzmann-Verteilung beschreibt die Geschindigkeitsverteilung der Moleküle in einem idealen Gas. Für den Betrag der Geschwindigkeiten gilt der Verlauf wie in der Skizze gezeigt. Die Kurven starten dabei im Nullpunkt, d.h. bei f (v = 0) = 0, wobei für höhere Temperaturen sich das Maximum der Kurven zu höheren Geschwindigkeiten verschiebt. Der Flächeninhalt unter den Kurven ist dabei konstant (Normierung), so dass, wenn die Kurven breiter werden, das Maximum kleiner wird. 2 Aufgabe 4: Silvesterparty (8 Punkte) Viele Menschen zelebrieren am Silvesterabend die Tradition des Bleigießens, um in die Zukunft blicken zu können. Der Brauch funktioniert wie folgt: In einem Edelstahllöffel werden M = 15g Blei erwärmt, bis es gerade vollständig geschmolzen ist. a) Welche Wärmemenge müssen Sie zuführen, wenn sich das Blei anfänglich auf Raumtemperatur T0 = 20◦ C befindet und der vordere Teil des Löffels (m = 5g) stets auf der Temperatur des Bleis ist? Welcher Anteil davon ist Schmelzwärme? b) Anschließend wird das Blei in ein Gefäß mit MW = 100g Wasser (Temperatur T0 ) gegossen. Welche Temperatur T haben Wasser und Blei nach vollständigen Wärmeausgleich? Hinweis: Vernachlässigen Sie die Erwärmung des Löffelstiels und sonstige Wärmeabgabe an die Umgebung; ZahkJ kJ kJ lenangaben: spezifische Wärmekapazitäten: cP b = 0, 13 kg·K , cEdelstahl = 0, 50 kg·K und cW asser = 4, 19 kg·K . kJ ◦ Spezifische Schmelzwärme von Blei: LP b = 25 kg . Schmelztemperatur von Blei: TP b = 327 C Lösung: a) Blei und Löffel müssen erwärmt werden. Zusätzlich muss das Blei geschmolzen werden: ∆Q = cP b · M · (TS − T0 ) + cEdelstahl · m · (TS − T0 ) + LP b · M = 1741J Der Anteil der Schmelzwärme ergibt sich zu: LP b ·M ∆Q = 0, 215 = 21, 5% b) Zur Erwärmung des Wassers trägt nur die Wärmemenge aus dem heißen Blei bei. Mit Energieerhaltung ergibt sich: cP b · M · (TS − T ) + LP b · M = cW asser · MW · (T − T0 ). Auflösen nach der Mischtemperatur T : P b ·M ·TS +cW ·MW ·T0 T = LP b ·M +c = 295, 3K = 22, 3◦ C cP b ·M +cW ·MW Aufgabe 5: Geladene Münzen (8 Punkte) (a) Wie groß ist die Gesamtladung aller Elektronen in einer Kupfermünze mit Masse m = 3g? (b) Von der Münze werde nun ein Elektron pro Atom auf eine zweite gleichartige Münze übertragen. Bei welchem Abstand der Münzen ist die Kraft zwischen ihnen genau so groß wie die Schwerkraft auf eine der Münzen auf der Erdoberfläche? Hinweis: Die Kernladungszahl und die molare Masse von Kupfer sind Z = 29 bzw. MCu = 63, 55g/mol; die Avogadrozahl ist NA = 6, 022 · 1023 /mol; die Münzen können als Punktladungen angenommen werden. Lösung: 3g = 2, 84·1022 , die Gesamtladung a) Die Gesamtanzahl von Kupferatomen NKu in einer Münze ist: NKu = NA · 63,55g Q in einer Münze also demzufolge: Q = NKu · 29 · e = 132, 1 kC b) Wenn pro Atom ein Elektron von einer Münze auf eine andere übertragen wird, hat die eine Münze die Ladung −NKu · e und die andere Münze die Ladung +NKu · e. Die Coulombkraft zwischen den beiden Münzen in Abhängigkeit ihres Abstands r lautet dann: 3 2 · e2 −NKu (−NKu · e) · (NKu · e) = 4πǫ0 r2 4πǫ0 r2 Da gelten soll: FC + Fg = 0, erhält man mit der Schwerkraft einer Münze auf der Erdoberfläche Fg = 0, 003 kg · g = (NKu · 63, 55 · u) · g: s FC = r= NKu · e2 = 2, 5 · 106 km 4πǫ0 · 63, 55 · u · g Aufgabe 6: Plattenkondensator (8 Punkte) (a) Ein mit Luft gefüllter Plattenkondensator (Fläche F , Plattenabstand d) wird bis zur halben Breite mit einem Dielektrikum (relative Dielektrizitätskonstante ǫ = 1, 5) aufgefüllt (siehe Skizze). Berechnen Sie die Kapazität des Kondensators. Hinweis: Das Problem kann auch mittels einer geeigneten Schaltung aus zwei Kondensatoren behandelt werden. (b) Nun wird ein zweiter ausschließlich mit Luft gefüllter Kondensator (Fläche F , Plattenabstand 2d) parallel zum Kondensator aus (a) geschaltet. Berechnen Sie die Gesamtkapazität der Anordnung. Lösung: a) Ersatzschaltung aus zwei hintereinandergeschalteten Kondensatoren (Breite d/2), einer davon leer (C1 = der andere mit dem Dielektrikum gefüllt (C2 = ǫ0 ǫ2A d ). Beide in Serie geschaltet ergibt: −1 C12 = C1−1 + C2−1 = ( ǫ0 2A d ), 2ǫǫ0 A −1 2ǫǫ0 A 2ǫ0 A −1 ) +( ) ⇒ C12 = d d (1 + ǫ)d b) Wenn parallel zu C12 noch ein weiterer leerer Kondensator C3 mit Fläche F und Plattenabstand 2d geschaltet wird, 0A , dann ergibt sich die Gesamtkapazität der Anordnung zu: d.h. C3 = ǫ2d Cges = C12 + C3 = (5ǫ + 1)ǫ0 A 2(ǫ + 1)d Aufgabe 7: Leiterschleife in zeitlich veränderlichem B-Feld (8 Punkte) Eine quadratische Leiterschleife mit Kantenlänge a befindet sich zur Hälfte in einem homogenen Magnetfeld, dessen Feldlinien senkrecht zur Flächennormalen der Leiterschleife aus der Zeichenebene herauszeigen (siehe Abbildung). Der Widerstand der Leiterschleife sei R (siehe Abbildung). Der Betrag des magnetischen Feldes B(t) als Funktion der Zeit sei wie folgt gegeben: B1 für t<0 t B(t) = B1 + B2 · t0 für 0 ≤ t ≤ t0 , B1 + B2 für t > t0 wobei B1 und B2 Konstanten sind. 4 (a) Skizzieren Sie B(t) als Funktion der Zeit. (b) Berechnen Sie die Stromstärke I(t), die durch die Leiterschleife fließt. (c) Geben Sie die Richtung des Stromes durch die Leiterschleife an, sowie die Richtung der Kraft, die auf die Leiterschleife wirkt. Begründen Sie Ihre Antwort. Lösung: a) ist klar. b) Es gilt (dA zeigt auch aus Zeichenebene heraus): Z a2 B(t) · dA = B(t) φm = 2 A ( 2 2 a 1 dφm (t) a2 dB(t) Uind (t) −B 2 t0 R =− · =− = I(t) = R R dt 2 R dt 0 für 0 ≤ t ≤ t0 sonst c) Aus der Lenzschen Regel ergibt sich, dass der Induktionsstrom seiner Ursache entgegenwirkt. Er fließt also so, dass das aus dem Strom resultierende Magnetfeld dem Magnetfeld B(t) entgegengerichtet ist. Aus der Rechten-HandRegel ergibt sich dann, dass die positiven Ladungen (= technische Strom) im Uhrzeigersinn fließen müssen. Alternativ: Wir haben dA so gewäht, dass es aus der Zeichenebene heraus zeigt. Damit wird das Wegintegral Uind = R E · dl gegen den Uhrzeigersinn entlang der Leiterschleife ausgeführt. Da Uind < 0, verläuft das Wirbel E-Feld im C Uhrzeigersinn und damit fließt der technische Strom auch in diese Richtung. Die Kraft auf die Leiterschleife ergibt sich aus F = ILxB. Die Kraft auf Ober-und Unterkante heben sich auf. Damit bleibt nur die Kraft übrig, die durch den Stromfluss durch die rechte Kante der Schleife verursacht wird. Aus der Rechten-Hand-Regel ergibt sich, dass diese die Schleife nach links aus dem Feld drückt. Aufgabe 8: Zwei Drähte (8 Punkte) Gegeben seien zwei lange Drähte im Vakuum, die im Abstand 2d parallel zur z-Achse verlaufen (siehe Abbildung). Auf beiden Drähten fließt ein Strom der Stärke I in positiver z-Richtung (aus der Zeichenebene heraus). Bestimmen Sie die Komponenten (Bx , By , Bz ) des magnetischen Feldes B im Punkt P. Lösung: Linker Draht: Bxl = − 1 µ0 I 1 1 µ0 I ·√ =− ·√ 2π 2π 2d 2d 2 By l = µ0 I 1 2π 2d 5 rechter Draht: µ0 I 1 2π 2d µ0 I 1 =− 2π 2d Bxr = − By r Gesamt: By = 0, Bz = 0 Bx = − µ0 I 1 2π d Aufgabe 9: Poynting-Vektor (8 Punkte) Das elektrische Feld einer ebenen elektromagnetischen Welle schwinge in y-Richtung. Der zugehörige Poynting~ sei gegeben durch S(x, ~ t) = A · cos2 (kx − ωt) · e~x . vektor S a) In welche Richtung breitet sich die Welle aus? b) Berechnen Sie das elektrische und das magnetische Feld der elektromagnetischen Welle. c) Berechnen Sie deren Wellenlänge und Frequenz. Lösung: a) Die elektromagnetische Welle breitet sich in x-Richtung aus. ~ = 1 (E ~ × B) ~ ~ = 1 |E| ~ ~ ⊥B ~ b) S |B| E µ0 c ~ = 1 |E| ~ · |B| ~ = ǫ0 c2 |E| ~ · |B| ~ = ǫ0 cE 2 ⇒ |S| µ 0 q q ~ A ~ = |S| ⇒ |E| ǫ0 c = ǫ0 c cos(kx − ωt) q A ~ = ey Richtung siehe Angabe ⇒ E ǫ0 c cos(kx − ωt) · ~ q ~ = 1 |E| ~ = 1 A cos(kx − ωt) |B| c c ǫ0 c ~⊥E ~ ⊥B ~ Das B-Feld schwingt in z-Richtung, da S ~ = ⇒B 1 c q A ǫ0 c cos(kx − ωt) · ~ez ~ ~ + λ, t0 ) c) Berechnung der Wellenlänge λ: Betrachte t0 = 0; E(x, t0 ) = E(x cos(kx) = cos(k(x + λ)) (= cos(2π + kx)) 2π ⇒ 2π + kx = k(x + λ) ⇒ λ = k (1) (2) ~ 0 , t) = E(x ~ 0 , t + T ), es sei x0 = 0 Berechnung der Frequenz f , betrachte E(x ⇒ cos(ωt) = cos(ω(t + T )) ωt + 2π = ω(t + T ) 2π 2π ω 1 T = ⇒ω= ⇒f = = ω T 2π T 6 (3) (4) (5) Aufgabe 10: Abbildung mit dünner Linse (8 Punkte) Die Skizze unten zeigt einen 1, 5 cm langen Gegenstand (dicker Strich) 6 cm vor einer Zerstreuungslinse mit einer Brennweite von −8 cm. a) Konstruieren Sie das Bild des Gegenstands. (Zeichnung des Strahlengangs) b) Berechnen Sie die Bildweite b (Abstand Bild-Linse) und die laterale Vergrößerung M (bzw. Verkleinerung) des Bildes. Lösung: a) b) Bildweite: 1 b = 1 f Vergrößerung: M = fg 1 −8·6 g ⇒ b = g−f = 6−(−8) − gb = 3,43 6 = 0, 57 − cm= −3, 43 cm 7