Energie, Arbeit, Leistung *82. Welche potenzielle Energie besitzt
Werbung

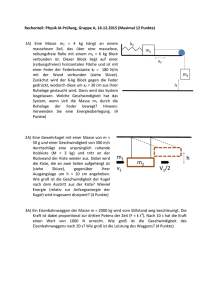
AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Energie, Arbeit, Leistung 82. Welche potenzielle Energie besitzt eine Person (Masse 75 kg), die sich 25 m über dem Erdboden befindet? 83. Auf welche Höhe kann eine Kugel der Masse 20 kg durch die Energie E = 10 kJ gebracht werden? 84. Welche Masse kann durch die Energie 20 kJ auf eine Höhe von 50 m über dem Erdboden gebracht werden? 85. Ein Körper wird durch die Kraft F = 2 kN um die Strecke s = 8 m verschoben. Wie groß ist der Arbeitsaufwand? 86. Ein Auto der Masse 800 kg wird 50 m weit geschoben. Bestimmen Sie den Arbeitsaufwand, wenn der Reibungsfaktor µ den Wert 0,20 besitzt. 87. Wie weit kann ein Auto von einer Tonne Masse durch einen Arbeitsaufwand von 100 kJ geschoben werden, wenn der Reibungsfaktor µ 0,18 beträgt? 88. Ein Auto (m = 800 kg) fährt mit der Geschwindigkeit 100 km/h. Bestimmen Sie seine kinetische Energie. 89. Mit welcher Geschwindigkeit (in km/h) fährt ein Wagen (900 kg), wenn er die kinetische Energie E = 200 kJ besitzt? 91. Ein Körper bewegt sich reibungsfrei aus eine Höhe von 2,0 m herab. Welche Geschwindigkeit kann er unten maximal erreichen? 92. Eine Kraft von 40 N dehnt eine Feder um 8 cm. Wie groß ist die in der gespannten Feder gespeicherte Energie? 93. Die Feder (Federkonstante D = 12 N/cm) einer Federpistole wird um 20 cm zusammengepresst. Beim Lösen der Feder wird eine Kugel der Masse 3,0 g beschleunigt. a) Wie groß ist die in der gespannten Feder gespeicherte Energie E? b) Welche Geschwindigkeit erreicht die Kugel? 94. Ein Akrobat mit 70 kg Masse fällt aus einer Höhe von 4 m auf ein Trampolin. Das Trampolin kann als Feder mit der Federkonstanten 4000 N/m betrachtet werden. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 1 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Mit welcher Geschwindigkeit trifft der Akrobat auf das Trampolin und wie weit wird dieses eingedrückt? 96. Ein Eisennagel der Masse 5 g wird durch die Kraft 2 kN 8 cm tief in ein Holzbrett getrieben. 40% der aufgebrachten Energie erwärmen dabei den Eisennagel mit der spezifischen Wärmekapazität c=0,452 kJ/kg K. Um wie viel Kelvin wird der Nagel erwärmt? 97. Ein Federpendel (D = 80 N/m) schwingt und besitzt eine Amplitude von ymax = 10 cm. Wie groß ist die in der Schwingung gespeicherte Energie E? 98. An einem Fadenpendel der Länge l=40 cm hängt eine Kugel (Masse 200 g). Die Kugel führt harmonische Schwingungen der Frequenz 0,6 Hz aus und besitzt eine Amplitude von 12 cm. Bestimmen Sie die potentielle Energie, die kinetische Energie, sowie die Gesamtenergie 5 Sekunden nach dem ersten Durchgang durch die Ruhelage. 100. Eine Eisenkugel (spezifische Wärmekapazität c = 0,452 kJ/kg K ) rollt über eine raue Fläche (Rollreibungszahl µ = 0,05). Nach 20 m kommt die Kugel zur Ruhe. Der Einfachheit halber wird angenommen, dass die vollständige Reibungsenergie zur Erwärmung der Kugel beiträgt. Um wie viel Kelvin erwärmt sich die Kugel? 101. Ein Wagen der Masse m = 1200 kg bewegt sich mit der Geschwindigkeit v = 200 km/h. Wie viel Liter Wasser ‐1 ‐1 (spezifische Wärmekapazität 4,2 kJ kg K ) kann durch die in der Bewegung gespeicherten Energie um 20 K erwärmt werden. 173. Ein Mauerstein mit der Masse von 2,4 kg fällt aus einer Höhe von 26 m herab und trifft mit einer ‐1 Geschwindigkeit von 18 ms auf die Erdoberfläche. Berechnen Sie den Anteil der mechanischen Energie, der während des Fallens in Wärme umgewandelt wird. Wie groß ist die dabei auftretende Temperaturerhöhung, wenn die Energieabgabe an die Luft vernachlässigt wird? 175. Bei einem Bremsvorgang verringert sich die kinetische Energie eines Fahrzeuges auf ein Drittel des Anfangswertes. In welchem Verhältnis stehen Endgeschwindigkeit und Anfangsgeschwindigkeit des Fahrzeuges? 177. Beim Hausbau wird zum Heben der Baumaterialien eine Zugvorrichtung benutzt, die aus einem Seil, einer festen Rolle, einer losen Rolle sowie einem Elektromotor besteht. Mit dieser Vorrichtung wird ein Balken der Masse 75 kg innerhalb von 12 s vom Boden senkrecht in das 6 m höher gelegene Dachgeschoss gehoben. a) Fertigen Sie eine Skizze der Zugvorrichtung an. b) Bestimmen Sie die vom Motor aufzubringende Zugkraft. c) Berechnen Sie die am Balken verrichtete Arbeit. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 2 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de d) Welche Leistung muss der Motor aufbringen? (Die Masse der Rolle und des Seiles wird vernachlässigt.) 178. Die potentielle Energie eines Fallschirmspringers verringert sich während des Sprunges. Bei geöffnetem Schirm nimmt seine kinetische Energie jedoch nicht zu. Wie ist das zu erklären? ‐1 ‐1 ‐1 181. Ein Auto (1000kg) wird von Null auf 36 kmh und dann von 36 kmh auf 72 kmh beschleunigt. Berechnen Sie für beide Beschleunigungsphasen die benötigte Energie. 220. Eine Feder wird durch eine Kraft von 4N um 15 cm gedehnt. a) Welche Arbeit ist notwendig, um die Feder auf 30 cm zu dehnen? b) Zeichnen Sie das Kraft‐Weg‐Diagramm für den Vorgang aus a). c) Das Dehnen der Feder von 15 cm auf 30 cm erfolgt in einer Zeit von 2 s. Berechnen Sie dafür die Leistung. ‐1 ‐1 221. Ein Auto (m=950kg) wird in 4s von v1 = 50 kmh auf v2 = 90 kmh beschleunigt. a) Welchen Weg legt es dabei zurück. b) Wie groß ist die Beschleunigungsarbeit? c) Welche Geschwindigkeit hätte der Wagen mit der gleichen Beschleunigungsarbeit erreicht, wenn er aus dem Stand beschleunigt wäre? ‐1 223. Eine an einem Ende fest eingespannte, waagerechte Feder (D = 10 N cm ) wird durch eine Druckkraft von 50 N vorgespannt. Am Ende dieser Feder liegt ein Holzklotz (m = 5,0 kg) auf waagerechter Unterlage. Die Gleitreibung zwischen Klotz und Unterlage wird durch den Reibungskoeffizienten 0,3 beschrieben. Die Feder wird freigegeben. a) Welche Energieumwandlungen finden in der Folge statt? b) Welche Geschwindigkeit hat der Klotz, wenn die Feder wieder entspannt ist? (Nutzen Sie zur Lösung den Teil a) 226. Welche Arbeit ist nötig, um 10 auf der Erde liegende Ziegelsteine von je 6,5 cm Höhe und 3,5 kg Masse aufeinander zuschichten? 227. Eine Lore der Masse 1 600 kg soll innerhalb von 2,5 min eine 190 m lange Strecke mit 16% Anstieg zurücklegen. Welche Antriebsleistung muss der Motor haben, wenn der Wirkungsgrad der Anlage durch Reibungsverluste nur 75% beträgt? 229. Begründe, warum der Quotient aus F und s als Maß für die mechanische Arbeit nicht sinnvoll wäre. 238. Ein Kran hebt eine Betonplatte der Masse 450 kg um 17 m. Berechne die verrichtete mechanische Arbeit. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 3 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 247. Ein Schlitten der Masse 60 kg startet aus der Ruhe von einem Hügel aus 5 m Höhe und erreicht den Fuß des ‐1 Hügels mit einer Geschwindigkeit von 6 ms . Welchen Betrag an Energie hat er durch Reibung usw. verloren? 267.a) Eine Masse m soll senkrecht auf die Höhe h gehoben werden. Zu diesem Zweck wird sie längs der ersten Teilstrecke h1 gleichförmig so beschleunigt, dass sie darüber hinaus noch um die zweite Teilstrecke h2 steigt. Welcher Ausdruck ergibt sich für die erforderliche Beschleunigung a? b) Ein Arbeiter wirft einen Sack mit der Masse 50 kg mit einem Kraftaufwand von 600 N auf die Schulter (Gesamthöhe 1,50 m). Welche Teilstrecke h1 hat er unter Kraftaufwand zu überwinden, und wie lange dauert der gesamte Vorgang? 273. Bei Bremsvorgängen vollziehen sich Energieumwandlungen. Ein LKW mit der Gesamtmasse 25t fährt mit konstanter Geschwindigkeit auf einer 18 km langen Strecke aus der Höhe 1800 m über dem Meeresspiegel bis auf 634 m Höhe herab. Bereits ohne Einsatz der Bremsen tritt ein bremsender Kraftbetrag (Fahrtwiderstand) von 5,0 % des Gewichtskraftbetrages auf. Berechnen Sie die Wärme, die die Bremsen des LKW bei der Abwärtsfahrt aufnehmen. 277. Gleich schwere Pakete werden vom Fußboden in ein Regal gehoben, dessen Fächer untereinander den gleichen Abstand haben. Welche der Arbeiten sind gleich groß? (siehe Abbildung) 286. Die zwei Pufferfedern eines Eisenbahnwagens (10 t Masse) werden um je 10 cm eingedrückt, wenn dieser mit der Geschwindigkeit 1 ms‐1 auf ein festes Hindernis prallt. Wie groß ist die Federkonstante einer jeden Feder? C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 4 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 294. Ein Bergsteiger mit der Masse 80 kg bewältigt einen Höhenunterschied von 120 m in 30 Minuten. Wie groß ist seine mechanische Leistung? (Rechne zuerst die Minuten in Sekunden um!) 297. In einem Wasserwerk wird ein Brunnen gebaut. Aus diesem sollen je Stunde 200 000 Liter Wasser gepumpt werden. Der Brunnen ist 8,0 m tief und soll zwei Pumpen erhalten. Von der Industrie werden Pumpen mit einer mechanischen Leistung von 1kW, 2kW, 2,5kW, 4kW und 10kW angeboten. Welche Pumpen würdest du bestellen? 301. Die groß ist die Leistung einer Pumpe, die in 10 Minuten 4000 l Wasser 5 m hochpumpt? 350. Eine Stahlkugel fällt aus 1,5m Höhe auf eine Stahlplatte und prallt von dieser mit der 0,55fachen Aufprallgeschwindigkeit zurück. a) Welche Höhe erreicht die Kugel nach dem ersten Aufschlag? b) Welche Zeit verstreicht vom Anfang der Bewegung bis zum 2. Aufschlag? 353. Wie viel Wasser fördert eine Pumpe von 75kW Leistung in 24 Stunden aus einem Schacht von 250m Tiefe? Wie viel Wasser fördert die Pumpe, wenn sie von einem Elektromotor betrieben wird, der eine Leistung von 120kW aufnimmt und einen Wirkungsgrad von 40% hat? 354. Ein Auto (Masse 900kg) nähert sich mit konstanter Geschwindigkeit von 90 km/h einer Steigung, als der Motor ausfällt. Wie lang darf der Anstieg (Steigungswinkel 8°) höchstens sein, damit das Auto das obere Ende der Steigung gerade noch erreichen kann? Welche Geschwindigkeit hat das Auto, wenn es die ersten 200m der Steigung zurückgelegt hat? 355. Die zwei Pufferfeder eines Eisenbahnwagens (Masse 10 Tonnen) werden um je 10cm eingedrückt, wenn dieser mit der Geschwindigkeit 1m/s auf ein festes Hindernis prallt. Wie groß ist die Federkonstante jeder Feder? 356. Die vertikal gehaltene Feder einer Federpistole wird durch Auflegen eines Massestücks von 500g um 5 cm zusammengedrückt und rastet dann ein. a) Wie groß ist die Federkonstante? b) Nun legt man einen Pfeil von 12g ein. Wie hoch wird er geschossen, wenn man Reibung und Federmasse vernachlässigt? Mit welcher Geschwindigkeit verlässt der Pfeil die Pistole? c) Die Pistole wird erneut geladen und nun in 1,25m Höhe über dem Boden waagrecht abgeschossen. Wie weit fliegt der Pfeil? Mit welcher Geschwindigkeit und unter welchem Winkel kommt er am Boden an? 357. An eine Feder mit der Federkonstanten D=100N/m wird eine Masse von 3kg gehängt. Dann wird die Feder um weitere 50cm nach unten ausgelenkt und losgelassen. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 5 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Welche Geschwindigkeit erreicht die Masse, wenn sie von der Feder 10cm hoch gezogen worden ist? 360. Bei einem Pumpspeicherwerk werden während der Nachtstunden (von 22 Uhr abends bis 6 Uhr morgens) 60 000 kWh aufgewendet, um das obere Rückhaltebecken zu füllen. Die Fallröhre hat eine Länge von 400 m, wobei der Höhenunterschied zwischen Pumpspeicherwerk und oberes Rückhaltebecken 220 m beträgt. Wie groß ist die angehobene Wassermenge in m³? 363. Welcher Wasserstrom in l/min ist erforderlich, wenn bei einem Gefälle von 4,5 m bei einer Wasserturbine eine Leistung von 70 kW abgenommen werden soll? Der Turbinenwirkungsgrad beträgt 80 %. 365. Beim Zusammenstellen eines Reisezuges wird ein Waggon mit 31 t Masse bereitgestellt. Er rollt einen Ablaufberg mit dem Neigungswinkel 1,7° von einer Höhe 1,0 m mit der Anfangsgeschwindigkeit 1,40 ms‐1 hinab und bewegt sich dann in der horizontalen Ebene geradlinig weiter. Entlang des gesamten Weges beträgt die mittlere Reibungszahl 0,0020. Berechnen Sie die Länge des horizontalen Weges, den der Waggon beim Ausrollen bis zum Stillstand fahren würde. 436. Ein Körper der Masse 1kg fällt aus einer Höhe h in 0,5 s frei zu Boden. a) Berechnen sie für die Zeitpunkte 0,1 s; 0,2 s; 0,3 s; 0,4 s und 0,5 s die potenziellen Energien bezüglich des Bodens und die kinetischen Energien des Körpers. b) Tragen sie in einem Diagramm über die Höhe h jeweils beide zugehörigen Energiewerte ein und verbinden sie die Punkte gleicher Energieformen. c) Addieren sie graphisch für einzelne Höhen h die potentiellen und kinetischen Energien! Machen Sie eine Aussage über die Summe der Energien. 467. Die Kugel eines Fadenpendels (l=1,2m) wird aus der Gleichgewichtslage um 60 cm ausgelenkt. Welche Geschwindigkeit muss die Kugel zusätzlich erhalten, damit sie nach dem Zurückschwingen eine Kreisbahn beschreibt? 485. Würde die Energie, die in einem Wasserkraftwerk „erzeugt“ wird, ausreichen, dass herabstürzende Wasser zu verdampfen (Die auftretenden Verluste bei den Energieumwandlungen werden vernachlässigt)? C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 6 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 501. In früheren Zeiten wurde als Arbeitskraft die Arbeit des Pferdes verwendet. Kurzzeitig schafft ein Pferd die Leistung von 1 PS (etwa 30 min lang), soll es aber 8 Stunden am Tag arbeiten, kommt es nur noch auf etwa 0,5 PS. Ein Göpel ist ein Vorrichtung, in der die Pferde im Kreis laufen müssen und dabei über eine Vorrichtung eine Welle antreiben. An der Welle wurde z.B. eine Pumpe angeschlossen, die Wasser aus einem Bergwerk pumpt. Wie viel Pferde bräuchte man, wenn damit eine 24h‐ Dauerleistung von 1 kW geleistet werden soll. 502. Mit Hilfe der dargestellten Anordnung lässt sich der Betrag der Geschwindigkeit einer Gewehrkugel bestimmen. Eine Gewehrkugel mit der Masse m=0,6 g trifft mit horizontaler Geschwindigkeit v auf einen Körper der Masse M=200,0 g. Der Körper besteht aus einem einseitig offenen Metallzylinder und einem Holzkern. Die Kugel dringt in den Kern ein und bleibt darin stecken. Der Zylinder bewegt sich reibungsfrei auf einer Führungsstange und drückt die Feder um die Strecke s zusammen. Die Federkonstante beträgt 70 N/m. a) Beschreiben Sie die Energieumwandlungen bis zum Ende des Zusammendrücken der Feder. b) Zeigen Sie, dass für den Betrag der Geschwindigkeit der Kugel vor dem Eindringen in den Körper gilt: v D s m M M m c) In einem Messversuch wir die Feder nach Aufprall des Körpers um s = 4,0 cm zusammengedrückt. Berechnen Sie die Geschwindigkeit der Kugel. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 7 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 513. In einem Wasserkraftwerk strömen aus einer Höhe von 70 m in der Minute 13000m³ Wasser und treiben über eine Turbine einen Generator an. Welche elektrische Leistung kann der Generator abgeben, wenn der Leistungsverlust der ganzen Anlage 15% beträgt? 526. Laut Auskunft der ÖSAG hat die Phyrnautobahn zwischen Gleinalmtunnel und Mautstelle St. Michael eine Steigung von 1,5%. Wenn man mit einem Citroen Evasion mit 1800 kg Gesamtgewicht diese Steigung hinunterrollen lässt, erreicht man eine Gleichgeschwindigkeit von 95 km/h. a) Berechne aus diesen Angaben die Fahrwiderstandskraft bei 95 km/h. b) Berechne unter Verwendung der berechneten Fahrwiderstandskraft die mechanische Leistung, die zum Antrieb des Fahrzeuges auf ebener Strecke mit 95 km/h erforderlich ist. c) Berechne aus dieser die mechanische Arbeit, die bei ebener Strecke nötig ist, um dieses Fahrzeug 100 km weit zu bewegen. d) Berechne daraus und unter der Annahme, dass das gegebene Fahrzeug bei 95 km/h einen Dieselverbrauch von rund 6,8 Liter pro 100 km hat, für diese Bedingungen den Wirkungsgrad. 547. Ein Tank soll mit Hilfe einer Pumpe mit Wasser gefüllt werden. Der Tank hat für den Schlauch zwei Anschlüsse, oben und unten. Wie verhält es sich mit der durch die Pumpe zu verrichteten Arbeit, um den Tank vollständig zu füllen. a) die Arbeit ist für den oberen und unteren Anschluss gleich groß. b) Die Arbeit ist beim Füllen durch den unteren Anschluss größer. c) die Arbeit ist beim Füllen durch den oberen Anschluss größer. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 8 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 673. Wie lange braucht eine Pumpe mit der Leistung 12 kW, um 15 000 Liter Wasser (m=15 000 kg) aus 15m Tiefe zu fördern? 674. Begründe, warum das Produkt aus W und t als Maß für die mechanische Leistung nicht sinnvoll wäre. 681. Stangenklettern im Sportunterricht Wer verrichtet mehr Arbeit? Berechne! Fred wiegt 35 kg und klettert 5 m hoch. Paul wiegt 43 kg und schafft nur 4m. 710. Frau Meier und Frau Schmidt wohnen im gleichen Haus genau übereinander. Beide haben auf ihren Fensterbrettern völlig gleiche Blumentöpfe. Die Töpfe von Frau Schmidt haben den doppelten Abstand zum Boden wie die Töpfe von Frau Meier. Beim Quatschen am Fenster stoßen beide Frauen im Eifer einen Blumentopf vom Fensterbrett. Vergleichen Sie die Aufschlaggeschwindigkeiten der beiden Töpfe. 725. Ein Hubschrauber hat eine Masse von 5,6 t und fliegt in 250 m Höhe mit 180 km/h. Vergleichen Sie seine potenzielle und kinetische Energie miteinander. 770. Eine Skiläuferin (m=50kg) fährt einen 40m langen Abhang mit dem Neigungswinkel von 40° hinab. Welche Geschwindigkeit und welche kinetische Energie erreicht sie am Fußpunkt des Hanges, wenn a) die Bewegung völlig reibungsfrei erfolgt? b)wenn Reibung mit einer Gleitreibungszahl f(gl)=0,1 vorliegt? Wie groß ist der Unterschied beider Energien? Wodurch wird diese Differenz hervorgerufen? 782. Ein Schlitten befindet sich in 20 m Höhe. Schlitten und Fahrer wiegen zusammen 45 kg. Am Ende der Abfahrt hat der Schlitten eine Geschwindigkeit von 10 km/h erreicht. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 9 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de a) Berechne die beiden mechanischen Energien. (4) b) Berechne den Wirkungsgrad in Prozent! (2) 783 Welche Energieform ist jeweils gespeichert? a) aufgeladener Akku b) Brot c) Wärmflasche d) Wasser im Stausee 784. Welche Energieumwandlungen findet jeweils statt - bei der elektrischen Zahnbürste - in der Solarzelle - beim Dynamo - Holzkohlengrill 791. Beim Bogenschießen wird ein Sportbogen verwendet, für den annähernd F~s² gilt. Dabei ist F Kraft, mit der der Bogen gespannt wird und s der Weg, um den der Pfeil dabei hach hinten gezogen wird. Um den Bogen um 5 cm zu spannen, ist eine Kraft von 10 N notwendig. a) Berechnen Sie die Kraft, die notwendig ist, damit der Bogen um 25 cm gespannt wird. b) Welche Energie ist bei dieser Spannung im Bogen gespeichert? c) Welche Höhe erreicht der Pfeil mit 50 g Masse, wenn er völlig regelfremd senkrecht nach oben angeschossen wird. C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 10 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 795. Wilhelm T., ein junger, talentierter Bogenschütze darf sich einen neuen Bogen kaufen. Er kann den Bogen mit maximal 50 N spannen und seine Arme reichen für einen Bogenauszug von 40 cm. Im Sportbogenfachgeschäft stehen jede Menge Bogen zur Verfügung. Zu jedem Bogen liegt ein Datenblatt vor, das den Zusammenhang zwischen der Kraft und dem Auszug darstellt. Welchen Bogen sollte sich Wilhelm kaufen? Begründen Sie die Wahl. 796. Für einen Bogen werden bei verschiedenen Kräften die dazu gehörigen Auszugswege gemessen. Danach wird ein Pfeil mit 25 g Masse eingelegt und abgeschossen. a) Zeichnen Sie das F‐s‐Diagramm. (s: Abszisse) b) Markieren Sie im Diagramm die im Bogen gespeicherte Energie. c) Bestimmen Sie mit dem grafischen Taschenrechner die Energie, die im Bogen gespeichert ist. d) Welche maximale Geschwindigkeit erreicht der Pfeil beim Abschuss? Kraft F in N Dehnung s in m 0 0,0 5 0,02 10 0,04 15 0,07 20 0,1 25 0,15 30 0,2 (Wenn Sie b) nicht gelöst haben, verwenden Sie für C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 11 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de die Energie im Bogen 15 J) 35 0,28 40 0,35 45 0,39 50 0,42 55 0,45 60 0,48 C:\Users\Udo\Desktop\Physik\Energie\Aufgaben1.doc 12