Bachelorarbeit von Marius Wilker - Ruhr

Bachelorarbeit
an der
Ruhr-Universität Bochum
Gewinnchancen
und
Gewinnerwartung
Marius Alexander Wilker
aus Marl
Bochum, im April 2008
Fakultät für Mathematik
Prof. Dr. R. Verfürth
Inhaltsverzeichnis
I. Einleitung ……………………………………………………………………………… 3
II. Beispiel Chuck-a-Luck ……..………………………………………………………… 3
II.1 Spielidee ..……………………………………………………………………. 3
II.2 Gewinnwahrscheinlichkeiten …..…...……………………………………….. 4
II.3 Einführung der Begriffe „Zufallsvariable“, „Erwartungswert“,
„Varianz“ und „Standardabweichung“ ……………………………………….. 6
II.3.1 Zufallsvariable …………………………………………………….. 6
II.3.2 Erwartungswert ……………………………………………………. 7
II.3.3 Varianz und Standardabweichung ………………………………… 9
II.4 Modifikation für eine faire Variante ………………………………………… 11
II.5 Spielstrategien ……………………………………………………………….. 13
III. Beispiel Roulette …………………………………………………………………..… 16
III.1 Spielmöglichkeiten …………………………………………………………. 16
III.2 Der Vorteil der Bank ………………………………………………….......... 18
III.3 Spielsysteme ………………………………………………………………... 21
III.3.1 Die „Martingale classique“ ……………………………………….. 21
III.4 Bernoulli-Experimente ……………………………………………………... 22
III.5 Gewinnerwartung der „Martingale classique“ ………………………………26
IV. Literaturverzeichnis …………………………………………………………………. 29
2
I. Einleitung
Schon seit Jahrhunderten begeistern sich die Menschen für alle möglichen Formen von
Spielen, insbesondere für das Glücksspiel. Mit Hilfe der Mathematik ist es uns möglich,
diese Spiele zu analysieren. Es können nicht nur Gewinnerwartungen für Glücksspiele
berechnet, sondern auch Spielstrategien für Spiele entwickelt werden, die nicht nur vom
Zufall abhängen. Bei der Analyse der Spiele bedienen wir uns eines weiten Bereichs
mathematischer Methoden wie zum Beispiel der Wahrscheinlichkeitstheorie und der
Kombinatorik.
Die folgende Arbeit basiert auf einem Seminarvortrag aus dem Seminar „Mathematik
und Spiel“, das im Wintersemester 2007/2008 von Prof. Dr. Rüdiger Verfürth gehalten
wurde. Inhalt dieses Seminars war es, mathematische Grundlagen von Spielen wie zum
Beispiel Schach, Poker, Lotto oder Monopoly zu erarbeiten.
Im Verlauf dieser Arbeit werden die beiden Glücksspiele „Chuck-a-Luck“ und „Roulette“ untersucht. Als Literatur für den ersten Teil, der sich mit dem Chuck-a-Luck beschäftigt, dient das Buch „Glück, Logik und Bluff“ von Jörg Bewersdorff aus dem Jahr
2007.
II. Beispiel Chuck-a-Luck
II.1 Spielidee
Chuck-a-Luck ist ein Glücksspiel, bei dem ein Spieler gegen die Bank spielt. Dabei
werden pro Spiel vom Spieler drei Würfel geworfen. Zuvor kann der Spieler auf eines
der sechs Würfelsymbole setzen. Trifft der Spieler mit den drei Würfeln einmal das
richtige Symbol, gewinnt er zusätzlich zu seinem Einsatz einen Einsatz dazu. Bei zwei
Treffern gewinnt der Spieler zusätzlich zu seinem Einsatz zwei Einsätze dazu und bei
drei Treffern gewinnt er drei zusätzliche Einsätze. Trifft der Spieler auf keinem der drei
Würfel das gesetzte Symbol, verliert er seinen Einsatz.
Im Folgenden soll Chuck-a-Luck auf seine Gewinnwahrscheinlichkeiten untersucht
werden. Denn wie bei jedem Glücksspiel stellt sich die Frage, ob die Bank im Vorteil
ist und wenn ja, wie stark? Obwohl Chuck-a-Luck im Vergleich zu anderen Glücksspielen, wie zum Beispiel Black Jack, ein recht überschaubares Glücksspiel ist, werden
die Gewinnchancen von Spielern oft überschätzt. Da der Spieler bei jedem Spiel auf
eines der sechs Symbole setzt und ihm zum Treffen des gesetzten Symbols drei Würfel
zur Verfügung stehen, könnte man denken, dass man bei jedem zweiten Spiel gewinnt.
3
Die Spieler sehen sich im Vorteil, da sie dabei nicht nur doppelt, sondern auch dreifach
und vierfach gewinnen können. Doch wie sich noch zeigen wird, ist dies ein Trugschluss.
II.2 Gewinnwahrscheinlichkeiten
Um die Gewinnchancen beim Chuck-a-Luck zu berechnen, muss man die Wahrscheinlichkeit für einen Gewinn und die jeweilige Höhe des Gewinns kennen. Es reicht also
nicht, nur die einzelnen Gewinnwahrscheinlichkeiten zu kennen, sondern man muss
auch die Höhe des Gewinns beachten. Der erste Schritt, um die Gewinnchancen des
Spielers zu berechnen, sieht wie folgt aus: Wir müssen zunächst die Wahrscheinlichkeiten für die möglichen Spielresultate berechen. Dazu betrachten wir einen LaplaceRaum, das heißt einen endlichen Wahrscheinlichkeitsraum, in dem alle Ergebnisse
gleich wahrscheinlich sind.
Definition:
Sei Ω ein endlicher Ergebnisraum. Wir definieren die LaplaceWahrscheinlichkeitsverteilung, kurz Laplace-Verteilung, auf Ω, indem
wir für ein Ereignis A C Ω
│A│
:
P(A) = ──
│Ω│
festlegen, wobei │A│ die Mächtigkeit der Menge A ist. Das Paar (Ω, P)
heißt Laplace-Raum.
Zur Berechnung der Wahrscheinlichkeiten beim Chuck-a-Luck betrachten wir den
Laplace-Raum
Ω = {(ω1, ω2, ω3)│ωi " {1, 2, 3, 4, 5, 6}}.
Die Mächtigkeit von Ω ist:
!
│Ω│= 63 = 216,
d. h. es gibt 216 verschiedene Würfelkombinationen.
Der nächste Schritt ist es nun, diese 216 Würfelkombinationen auf ihre Anzahl der richtigen Treffer zu überprüfen. Die Anzahl der richtigen Treffer kann man natürlich von
der Bedeutung mit der Höhe des Gewinns gleichsetzen.
4
In der folgenden Tabelle sind die einzelnen Gewinnwahrscheinlichkeiten beispielhaft
für einen einfachen Einsatz auf die Sechs dargestellt.
Gewinnhöhe
Würfelkombinationen
Wahrscheinlichkeit
_A_
4
6_6_6
3
6 _ 6 _ a, 6 _ a _ 6, a _ 6 _ 6 mit a _ {1, 2, 3, 4, 5}
2
0
6 _ a _ b, a _ 6 _ b, a _ b _ 6 mit a,b _ {1, 2, 3, 4, 5}
6 _ a _ b, a _ 6 _ b, a _ b _ 6 mit a,b _ {1, 2, 3, 4, 5}
gesamt
1
1/216
15
15/216
75
125
75/216
125/216
216
1
Tabelle 1: Gewinnwahrscheinlichkeit beim Chuck-a-Luck und Einsatz auf die Sechs
Die Gewinnwahrscheinlichkeiten für die einzelnen Spielresultate beim Chuck-a-Luck
sind nun bekannt. Doch wie kann man daraus die Gewinnchancen des Spielers berechnen? Gesucht wird also das Verhältnis, in dem über lange Zeit der durchschnittliche
Gewinn zum Einsatz steht. Wenn dieses Verhältnis bekannt ist, kann eine konkrete
Aussage darüber gemacht werden, ob die Bank im Vorteil ist.
Um die Gewinnchancen des Spielers zu berechnen, muss jede Gewinnhöhe mit ihrer
relativen Häufigkeit multipliziert werden. Diese Produkte werden anschließend addiert
und die Summe, die sich ergibt, ist der durchschnittliche sich auf Dauer einstellende
Gewinn des Spielers beim Chuck-a-Luck. Konkret ergibt sich der Wert
1
15
75
125
199
·4+
·3+
·2+
·0=
= 0,9213.
216
216
216
216
216
Da dies etwa 8% weniger sind als der Einsatz, ist die Bank beim Chuck-a-Luck deutlich
im Vorteil.
5
II.3 Einführung der Begriffe „Zufallsvariable“, „Erwartungswert“,
„Varianz“ und „Standardabweichung“
II.3.1 Zufallsvariable
Für den weiteren Verlauf ist es wichtig, zunächst einige Begriffe einzuführen. Der erste
Begriff ist die Zufallsvariable. Zufallsvariablen spielen eine wichtige Rolle bei der Beschreibung von Zufallsexperimenten. Andere Begriffe, die manchmal für eine Zufallsvariable benutzt werden, sind zufällige Variable, Zufallsgröße und zufällige Größe.
Eine Zufallsvariable ist einfach gesagt eine veränderliche Größe, deren Wert vom Zufall abhängt. Beim Chuck-a-Luck werden die Zahlenwerte 0, 2, 3 und 4 zufällig angenommen. In dem bereits eingeführten Laplace-Raum Ω entsprechen die Elemente
ω " Ω den möglichen Ergebnissen des Zufallsexperimentes. Die Zufallsvariable ist
also eine Zuordnungsvorschrift X, die jedem Ergebnis ω des Experimentes eine reelle
!
Zahl x zuordnet. Kurz gesagt handelt es sich bei einer Zufallsvariablen also um eine
Funktion X: Ω → R.
Natürlich kann man auch die Wahrscheinlichkeit, dass ein Wert x " X angenommen
wird, berechnen. Fürs Chuck-a-Luck wurden die einzelnen Wahrscheinlichkeiten bereits in Tabelle 1 zusammengefasst. In unserem Fall kann man also für die Zufallsvari!
able X, die zufällig die Werte 0, 2, 3 und 4 annimmt, die so genannte
Wahrscheinlichkeitsverteilung, folgendermaßen schreiben:
P(X = 0) =
125
216
P(X = 2) =
75
216
P(X = 3) =
15
216
P(X = 4) =
1
216
Ebenso kann man mit der Wahrscheinlichkeitsverteilung auch die Wahrscheinlichkeit
für eine Teilmenge A " R berechnen. So wäre zum Beispiel die Wahrscheinlichkeit,
dass der Spieler mindestens mit einem der drei Würfel die gesetzte Zahl trifft
P(X " A) =
!
91
, mit A = {2, 3, 4}.
216
!
6
II.3.2 Der Erwartungswert
Im Beispiel des Chuck-a-Luck wurden die Gewinnchancen direkt aus den möglichen
Gewinnhöhen und den ihnen zugeordneten Wahrscheinlichkeiten berechnet. Mathematisch wurde der so genannte Erwartungswert berechnet.
Definition:
Für eine Zufallsgröße X, die nur endlich viele Werte x1, x2, …, xn annehmen kann, definieren wir den Erwartungswert E(X) durch
n
E(X):=
!
i =1
P(X = xi) · xi .
Allgemein kann man sagen, dass der Erwartungswert des Gewinns, kurz, die Gewinnerwartung, bei der Analyse von Spielen eine zentrale Bedeutung erhält. Bei Spielen, die
strategisch beeinflusst werden können, sollte man sich so verhalten, dass die Gewinnerwartung maximal wird. Die folgenden Sätze geben uns Rechenregeln an die Hand,
die uns die Berechnung des Erwartungswertes von Zufallsvariablen erheblich erleichtern.
Satz: (Linearität des Erwartungswertes) Es seien X und Y zwei Zufallsvariablen, deren Erwartungswerte existieren. Dann gilt für a, b " R
(i)
E(aX + b) = aE(X) + b,
(ii)
E(X + Y) = E(X) + E(Y).
!
Die folgende Definition ist für den nächsten Satz notwendig:
Definition:
Die Zufallsvariablen X1, …, Xn heißen unabhängig, wenn für alle Intervalle I1, …, In C R gilt
n
P(X1 " I1, …, Xn " In) =
!
!
!
i =1
P(Xi " Ii).
!
Satz: (Multiplikationsgesetz) Für zwei unabhängig Zufallsvariablen X und Y gilt
E(XY) = E(X)·E(Y),
sofern die Erwartungswerte E(X) und E(Y) existieren.
7
Beispiele zum Erwartungswert:
a) Für den Erwartungswert eines einfachen Würfelwurfes mit einem regulären SechserWürfel ergibt sich der Wert
6
E(X) =
1
P(X = xi) · xi =
6
!
i =1
6
!
i =1
xi =
1
1
· (1+2+3+4+5+6) = · 21 = 3,5.
6
6
b) Für den Erwartungswert der Summe zweier Würfelwürfe mit einem regulären Sechser-Würfel ergibt sich der Wert
12
E(X) =
!
i=2
=
P(X = xi) · xi
1
2
3
6
·2+
·3+
·4+…
· 7 + ..
36
36
36
36
.. +
3
2
1
· 10 +
· 11 +
· 12 = 7.
36
36
36
c) Das letzte Beispiel ist etwas außergewöhnlicher. Es geht darum, den Erwartungswert
eines Kandidaten der bekannten TV-Quiz-Show „Wer wird Millionär?“ zu berechnen,
wenn er sich auf der Gewinnstufe 125.000 € befindet und sich an dieser Stelle zufällig
für eine der vier Antwortmöglichkeiten entscheidet. Dabei betrachten wir die ältere
Version des Quiz, bei dem der Kandidat bei falscher Antwort auf die Gewinnstufe
16.000 € zurückfällt. An dieser Stelle fällt der Kandidat mit einer Wahrscheinlichkeit
von ¾ auf die Gewinnstufe 16.000 € zurück. Jedes vierte Mal erreicht er allerdings die
Gewinnstufe 500.000 €. Folglich ergibt sich der Erwartungswert
4
E(X) =
!
i =1
P(X = xi) · xi =
3
1
· 16.000 € + · 500.000 € = 137.000 €
4
4
für den Kandidaten. Im Durchschnitt gewinnt der Kandidat an dieser Stelle bei völliger
Ahnungslosigkeit 12.000 € mehr, als er gewinnen würde, wenn er sich dazu entschließt,
nicht zu antworten und die sicheren 125.000 € zu kassieren. Nicht zu vergessen ist, dass
er zusätzlich auch noch die 500.000 € – Frage zu sehen bekommt, dessen Antwort er
möglicherweise auch kennt.
Noch eindeutiger wird es, wenn der Kandidat noch den 50:50 – Joker besitzt. Dann
ergibt sich für den Kandidaten der Erwartungswert
8
2
E(X) =
!
i =1
P(X = xi) · xi =
1
1
· 16.000 € + · 500.000 € = 258.000 €.
2
2
II.3.3 Varianz und Standardabweichung
Durch die Berechnung des Erwartungswertes werden die möglichen Ergebnisse eines
Spiels gut zusammengefasst. Der Spieler hat mit der Kenntnis über den Erwartungswert
einen guten Überblick, in welchem Bereich sich die Ergebnisse durchschnittlich bewegen. Allerdings reicht die alleinige Betrachtung des Erwartungswertes zur Beschreibung eines Zufallsexperimentes bzw. eines Spiels nicht aus. Denn es gehen wichtige
Informationen darüber verloren, wie weit die Werte auseinander liegen. Um diese Information zu beschreiben, gibt es den Begriff der Streuung. Die Streuung ist ein Maß
dafür, wie stark und wie wahrscheinlich die Werte um den Erwartungswert schwanken.
Mathematisch wird die Streuung einer Zufallsvariablen X durch die transformierte Zufallsgröße │X – E(X)│ beschrieben. Der Erwartungswert
E(│X – E(X)│)
dieser transformierten Zufallsvariable, die genau die Angaben darüber enthält, welche
absoluten Abweichungen vom Erwartungswert möglich sind und wie wahrscheinlich
sie eintreten, ist ein mögliches Maß für die Streuung. Um den Begriff der Streuung etwas zu verdeutlichen, folgt zunächst ein Beispiel:
Der Erwartungswert für die Augenzahl eines einfachen Würfelwurfes ist mit E(X) = 3,5
bekannt. Für die Streuung der Augenzahlen eines einfachen Würfelwurfes ergibt sich
der Wert
E(│X – E(X)│)
6
=
!
i =1
P(│X – 3,5│ = │xi – 3,5│) ·│xi – 3,5│
1
=
6
=
6
! │xi – 3,5│
i =1
1
(2,5 + 1,5 + 0,5 + 0,5 + 1,5 + 2,5)
6
= 1,5.
9
Hier wurde die Streuung, wie bereits erwähnt, als mittlere Abweichung vom Erwartungswert dargestellt. Dies ist eine Möglichkeit. In der Regel wird die Streuung allerdings mit der so genannten Standardabweichung
! X = E (( X ! E ( X )) 2 )
gemessen. Dies liegt ausschließlich daran, dass Absolutbeträge, wie sie eben benutzt
wurden, mathematisch ungünstiger zu handhaben sind. Diesem Problem geht man
durch das Quadrieren der einzelnen Abweichungen der Werte der Zufallsvariable X
von ihrem Erwartungswert aus dem Weg. Den Radikand nennt man auch Varianz der
Zufallvariablen X. Sie wird mit Var(X) bezeichnet. Zusammengefasst wird dies in der
folgenden Definition.
Definition:
Es sei X eine Zufallsvariable, für die E(X – E(X))2 existiert. Dann definieren wir die Varianz von X als
Var(X):= E(X – E(X))2.
Als Symbol für die Varianz wird oft σ2 bzw. σ2X verwendet. Die Wurzel
der Varianz heißt Standardabweichung.
Auch für die Varianz und die Standardabweichung soll noch mal das Beispiel des einfachen Würfelwurfes betrachtet werden. Für die Varianz ergibt sich
Var(X) = ! 2 X
6
=
!
i =1
P( (X – 3,5)2 = (xi – 3,5)2) · (xi – 3,5)2
1
=
6
=
6
!
i =1
(xi – 3,5)2
1
[(-2,5)2 + (-1,5)2 + (-0,5)2 + (0,5)2 + (1,5)2 + (2,5)2)]
6
=
1
(6,25 + 2,25 + 0,25 + 0,25 + 2,25 + 6,25)
6
=
1
· 17,5 ≈ 2,917.
6
Für die Standardabweichung ergibt sich daher der Wert σX = 1,708.
10
Wir sehen, dass der Wert, den wir zuerst für die Streuung ausgerechnet haben, nicht mit
dem eben berechneten Wert für Standardabweichung übereinstimmt. Daher ist es wichtig, immer denselben Ausdruck für die Streuung zu verwenden. Wie bereits erwähnt,
bietet sich hier die Standardabweichung eher an, da es bei der Standardabweichung
vermieden wird, mit den mathematisch ungünstigeren Absolutbeträgen zu rechnen.
Abschließend werden noch die Rechenregeln für die Varianz bzw. die Standardabweichung in den beiden folgenden Sätzen zusammengefasst.
Satz: Es sei X eine Zufallsvariable und a, b " R mit a ≥ 0. Dann gilt für die Varianz
bzw. für die Standardabweichung
(i)
bzw.
Var(aX + b) = a2·Var(X)
!
! aX +b = a · ! X
Var(X) = E(X2) – (E(X))2.
(ii)
Satz: Für unabhängige Zufallsvariablen X1, ..., Xn gilt
Var(X1 + … + Xn) = Var(X1) + … + Var(Xn)
bzw.
! X 1 +...+ X n =
! 2 X 1 + ... + ! 2 X n
Das heißt die Varianz einer Summe unabhängiger Zufallsvariablen ist gleich der
Summe der Varianzen.
II.4 Modifikation für eine faire Variante
Ein Glücksspiel wird als fair bezeichnet, wenn der Einsatz und der durchschnittliche
Gewinn übereinstimmen. Chuck-a-Luck ist demnach nicht fair, denn
E (X) =
199
≠ 1.
216
Wir können Chuck-a-Luck allerdings so anpassen, dass es fair ist. Dazu muss man allerdings zunächst verstehen, warum die Bank überhaupt im Vorteil ist.
Wie bereits erwähnt wurde, würfelt man durchschnittlich in jedem zweiten Spiel einen
Treffer. Dies kann man leicht zeigen, indem man den Erwartungswert für die durch11
schnittliche Anzahl von Treffern in einem Spiel berechnet. Dazu müssen wir die relativen Häufigkeiten der einzelnen Spielresultate, die bereits in Tabelle 1 beispielhaft für
einen einfachen Einsatz auf die Sechs berechnet wurden, mit der jeweiligen Anzahl von
Treffern multiplizieren und anschließend die Produkte addieren. Als Erwartungswert
für die durchschnittliche Anzahl von Treffern in einem Spiel ergibt sich
E(X) =
1
15
75
125
1
·3+
·2+
·1+
·0= .
216
216
216
216
2
An dieser Stelle ist es wichtig zu beachten, dass die Zufallsvariable X in diesem Fall
eine andere ist. Bisher wurden von der Zufallsvariable X im Beispiel des Chuck-a-Luck
immer die Werte der Gewinnhöhen (0, 2, 3, 4) zufällig angenommen. In der letzten
Berechnung nimmt die Zufallsvariable X aber zufällig die mögliche Anzahl der Treffer
(0, 1, 2, 3) in einem Chuck-a-Luck Spiel an.
Derselbe Erwartungswert ergibt sich auch mit den Rechenregeln für den Erwartungswert:
E(X) = E(XWurf 1) + E(XWurf 2) + E(XWurf 3) =
1
1
1
1
+
+ = .
6
6
6
2
Hier stellt sich die Frage, warum der Erwartungswert für den durchschnittlichen Gewinn bei einer Chuck-a-Luck Partie nicht eins ist, obwohl man jedes zweite Mal die
gesetzte Zahl trifft.
Zur Erklärung machen wir zunächst eine Vorüberlegung. Wir stellen uns die Frage, wie
viel wir pro Treffer gewinnen müssen, damit sich Einsatz und Gewinn ausgleichen?
Die Antwort ist eindeutig: Wenn man jedes zweite Mal die gesetzte Zahl trifft, gleichen sich Einsatz und Gewinn bei einer Gewinnhöhe von zwei Einsätzen pro Treffer
aus. Was soviel bedeutet, dass man jedes zweite Mal einen Einsatz verliert, dafür aber
die anderen Male im Durchschnitt zwei Einsätze gewinnt. Dabei ist zu beachten, dass
man bei einem Gewinn von zwei Einsätzen nur einen Einsatz netto gewinnt.
Beim Chuck-a-Luck ist dies nur bei der Gewinnhöhe für einen Treffer der Fall. Hier
erhalten wir für einen Treffer zwei Einsätze. Bei zwei Treffern erhalten wir lediglich
drei Einsätze. Nach unserer Vorüberlegung sollte man für zwei Treffer allerdings vier
Einsätze gewinnen. Gleiches gilt für drei Treffer – hier erhalten wir vier Einsätze, obwohl sechs nötig wären, um im Durchschnitt ein ausgeglichenes Verhältnis von Einsatz
und Gewinn zu erhalten. Würde man die Gewinnhöhen entsprechend der Vorüberlegung anpassen, würde sich ein Erwartungswert von
12
E(X) =
1
15
75
125
·6+
·4+
·2+
·0=1
216
216
216
216
ergeben, und das Spiel wäre fair.
II.5 Spielstrategien
Im Verlauf dieser Arbeit wurde bereits gezeigt, wie man mit Zufallsvariablen rechnet.
Dabei haben wir gesehen, dass der Erwartungswert linear ist und dass das Multiplikationsgesetz gilt. Um hierfür ein paar praktische Beispiele zu geben, betrachten wir Zufallsgrößen, wie sie sich aus den Ergebnissen von zwei aufeinander folgenden Chuck-aLuck Partien ableiten.
Dabei bezeichnet X1, X2, …, X6 den Gewinn, wenn man beim ersten Wurf einen einfachen Einsatz auf die Eins, Zwei, … bzw. Sechs setzt. Gleiches gilt bei den Zufallsvariablen Y1, Y2, …, Y6 für den zweiten Wurf.
Wie man leicht erkennen kann, sind die zwei Zufallvariablen Xi und Yi stets voneinander unabhängig. Das heißt, dass der Wert, den die Zufallsvariable Xi annimmt, nicht
durch den Wert, den die Zufallsvariable Yi annimmt, beeinflusst wird und umgekehrt.
So kann es zum Beispiel sein, dass X1 und Y6 beide zugleich den Maximalwert 4 erreichen. Anders ist dies für zwei verschiedene Zufallsvariablen Xi und Xj oder Yi und Yj.
Diese Zufallsvariablen sind voneinander abhängig. Es ist unmöglich, dass zum Beispiel
X1 und X6 beide zugleich den Maximalwert 4 erreichen. Die dafür notwendigen Würfelergebnisse 1-1-1 und 6-6-6 schließen sich gegenseitig aus.
Im Folgenden werden die Ausdrücke
2X6, X6 – 1, X1 + X6, X6 + Y6 und X6Y6
betrachtet.
Mathematisch handelt es sich bei den Ausdrücken um die Addition, Subtraktion und
Multiplikation von Abbildungen, die einen gemeinsamen Definitionsbereich besitzen.
Bevor die Ausdrücke mathematisch auf ihren Erwartungswert und später auch auf ihre
Varianz untersucht werden, sollen sie zunächst in der folgenden Tabelle praktisch gedeutet werden.
13
Praktische Deutung
Ausdruck
2X6
X6 - 1
Der Gewinn, wenn bei ersten Wurf ein doppelter Einsatz auf die Sechs gesetzt wird
Der möglicherweise negative Gewinnsaldo, wenn bei einem einfachem Einsatz auf die
Sechs im ersten Wurf vom Gewinn der Einsatz abgezogen wird
X1 + X6
Der Gesamtgewinn, wenn jeweils einfach auf die Eins und die Sechs gesetzt wird
X6 + Y6
Der Gesamtgewinn, wenn bei beiden Würfen jeweils einfach auf die Sechs gesetzt wird
X6Y6
Der Gewinn, wenn beim ersten Wurf auf die Sechs gesetzt wird und der eventuelle Gewinn
für den nächsten Wurf stehen bleibt und somit auch auf die Sechs gesetzt wird
Tabelle 2: Praktische Deutung verschiedener Ausdrücke
Mit Hilfe der Rechenregeln ergeben sich folgende Erwartungswerte für die fünf Zufallsvariablen:
E(2X6) = 2 E(X6)
E(X6 – 1) = E(X6) – 1
= 1,843
= – 0,079
E(X1 + X6) = E(X1) + E(X6)
= 1,843
E(X6 + Y6) = E(X6) + E(Y6)
= 1,843
E(X6Y6)
= E(X6) · E(Y6)
= 0,849.
Bei den ersten vier Ausdrücken erhalten wir nahezu denselben Erwartungswert. Lediglich
E(X6 – 1) weicht ab, was damit zusammenhängt, dass der Einsatz bereits abgezogen ist.
E(X6Y6) fällt etwas aus der Reihe, da hier die Erwartungswerte von zwei unabhängigen Zufallsvariablen miteinander multipliziert werden. Außerdem werden hier mit einem Einsatz
zwei Runden gespielt. Hierbei muss man beachten, dass in der zweiten Runde der Gewinn der
ersten Runde, der im Durchschnitt bei 0,92 liegt, gesetzt wird. Daher liegt der Verlust bei
zwei Runden, im Gegensatz zu den anderen Strategien, bei durchschnittlich 0,151 Einsätzen.
Bei den Zufallsvariablen, die den Erwartungswert 1,843 haben, liegt der durchschnittliche
Verlust logischerweise bei 0,157 Einsätzen. Hier werden immer mit zwei Einsätzen insgesamt
zwei Runden gespielt. Dabei kommt es aber auch vor, dass beide Einsätze in derselben Runde
gesetzt werden. Wichtig ist es, sich dessen bewusst zu sein, dass man, egal für welche Spielstrategie man sich entscheidet, immer für einen ganzen Einsatz pro Runde etwa 8% verliert.
In der folgenden Tabelle sind die verschiedenen Spielstrategien mathematisch untersucht
worden.
14
t
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
!
P(2X 6 = t)
P(X 1+X6 = t)
P (X 6+Y 6 = t)
P(X 6-1 = t)
P(X6Y 6 = t)
0,578703704
0,57870
0,34722
0,29630
0,33490
0,44444
0,11111
0,12037
0,02778
0,82251
0,34722
0,06944
0,00463
0,40188
0,08038
0,12592
0,04823
0,00804
0,00064
0,00002
0,06944
0,00463
0,12056
0,04823
0,00322
0,00482
0,00064
1,00000
1,00000
1,00000
1,00000
0,00002
1,00000
E(X)
1,842593
1,842593
1,842593
-0,078704
0,848787
Var(X)
4,956704
2,003001
2,478352
1,239176
3,639150
_X
2,226366
1,415274
1,574278
1,113183
1,907656
Tabelle 3: Mathematische Untersuchung der fünf verschiedenen Spielstrategien
Die Tabelle gibt Aufschluss darüber, wie sich die einzelnen Spielstrategien voneinander unterscheiden. Besonders interessant ist es, die drei Spielstrategien links vom Trennstrich zu
betrachten, denn alle drei haben denselben Erwartungswert. Auch der zweifache Einsatz ist
bei allen gleich. Es fällt auf, dass sich die drei Spielstrategien in der Risikobereitschaft, für die
die Varianz bzw. die Standardabweichung stehen, unterscheiden.
Dabei steht 2X6 für ein hohes Risiko, denn die Varianz ist mit dem Wert 4,96 am größten. Bei
dieser Strategie gewinnen wir mit einer Wahrscheinlichkeit von 0,579% nichts. Allerdings
kann man bis zu 8 Einsätze gewinnen. Dieser maximale Gewinn wird durchschnittlich jedes
216. Mal ausgezahlt.
Die Zufallsvariable X1 + X6 bürgt ein geringes Risiko mit sich, denn die Varianz ist mit dem
Wert 2,00 am geringsten. Wir verlieren nur zu 0,296% unsere kompletten zwei Einsätze und
erzielen immerhin durchschnittlich jedes 36. Mal den Maximalgewinn von 5 Einsätzen.
Für ein mittleres Risiko steht die Strategie X6 + Y6. Hier beträgt die Varianz 2,48. Dabei wird
zu 0,335% nichts gewonnen. Jedoch können bis zu 8 Einsätze gewonnen werden. Dies ist aber
weitaus unwahrscheinlicher als bei der ersten Strategie.
15
III. Beispiel Roulette
III.1 Spielmöglichkeiten
Roulette ist das beliebteste Casino-Glücksspiel der Welt. Auf dem Rouletterad (Cuvette) befinden sich die Zahlen 1 – 36 und je nach Variante noch ein oder zwei weitere Zahlen; und
zwar die Null (Zero) bzw. die Null und die Doppel-Null. Die 36 Zahlen sind in einer bestimmten Reihenfolge unregelmäßig auf dem Rouletterad verteilt und haben im Wechsel die
Farben Rot und Schwarz. Die Null und Doppel-Null sind grün.
Bild 1: Rouletterad
Beim Roulette versucht der Spieler, im Vorhinein zu erraten, auf welche Zahl oder Farbe (rot
oder schwarz) die Kugel im Rouletterad fällt. Dabei gibt es verschiedene Setzmöglichkeiten,
die später noch erläutert werden. Wie bereits erwähnt, gibt es verschiedene Varianten des
Roulettes. Die zwei bekanntesten Varianten des Roulettes sind zum einen das Französische
oder Europäische Roulette und zum anderen das Amerikanische Roulette. Der Hauptunterschied der beiden Formen ist, dass es beim Französischen Roulette 37 Ereignisse gibt (1 – 36,
0), im Gegensatz zum Amerikanischen Roulette mit 38 Ereignissen (1 – 36, 0, 00). In den
europäischen Casinos wird das Amerikanische Roulette allerdings auch mit 37 Zahlen angeboten. Hier liegt der Unterschied dann nur noch im Ablauf des Spiels und den Auszahlungsreglungen für den Fall, dass die Kugel auf die Null fällt.
Im weiteren Verlauf der Arbeit sollen zunächst die verschiedenen Wettmöglichkeiten vorgestellt werden. Dabei wird auch erwähnt, wie hoch ein möglicher Gewinn wäre. Es handelt sich
immer um Vielfache des Einsatzes. Alle Wettmöglichkeiten gelten sowohl fürs Französische,
wie auch fürs Amerikanische Roulette.
16
Beim Roulette werden einfache und mehrfache Chancen unterschieden. Bei den einfachen
Chancen wird dem Spieler im glücklichen Fall ein 1:1-Gewinn ausbezahlt. D. h. er erhält zusätzlich zu seinem Einsatz einen weiteren Einsatz und hat sein Geld somit verdoppelt.
Einfache Chancen:
-
Rouge (Rot, engl. Red) und Noir (Schwarz, engl. Black)
-
Pair (Gerade, engl. Even) und Impair (Ungerade, engl. Odd)
-
Manque (Niedrig, engl. 1–18) und Passe (Hoch, engl. 19–36).
Mehrfache Chancen:
-
Plein, engl. Full number: Man setzt auf eine der 37 Zahlen; die Auszahlungsquote beträgt 35:1.
-
Cheval, engl. Split: Man setzt auf zwei auf dem Tableau benachbarte Zahlen, z. B. 0/2
oder 13/14 oder 27/30, die Auszahlungsquote beträgt 17:1.
-
Transversale pleine, engl. Street: Man setzt auf die drei Zahlen einer Querreihe des
Tableaus, also z. B. 19, 20 und 21; die Auszahlungsquote beträgt 11:1.
-
Carré, engl. Corner: Man setzt auf vier auf dem Tableau angrenzende Nummern, z. B.
23/24/26/27; die Auszahlungsquote beträgt 8:1. Dabei ist es auch möglich, auf die ersten vier Zahlen, d. h. auf 0, 1, 2 und 3, zu setzen. Der gesonderte Ausdruck hierfür lautet: Les quatre premiers, engl. First four.
-
Transversale simple, engl. Six line: Man setzt auf die sechs Zahlen zweier aufeinander
folgender Querreihen des Tableaus, z. B. auf die Zahlen 4, 5, 6, 7, 8 und 9; die Auszahlungsquote beträgt 5:1.
-
Douzaines, engl. Dozens: Die Zahlen 1–36 sind in drei Dutzende eingeteilt; die Gewinnquote beträgt jeweils 2:1.
-
-
12P, Premier, engl. First dozen. Erstes Dutzend, die Zahlen 1–12
-
12M, Milieu, engl. Second dozen. Mittleres Dutzend, die Zahlen 13–24
-
12D, Dernier, engl. Third dozen: Letztes Dutzend, die Zahlen 25–36.
Colonnes, engl. Columns: Man setzt auf die im Tableau senkrechten Reihen. Eine Kolonne wird aus zwölf Zahlen gebildet; die Gewinnquote beträgt wie bei den Dutzenden
2:1.
-
Colonne 34: Die erste Kolonne umfasst die Zahlen 1, 4, 7, 10, ..., 34
-
Colonne 35: Die mittlere Kolonne umfasst die Zahlen 2, 5, 8, 11, ..., 35
-
Colonne 36: Die letzte Kolonne umfasst die Zahlen 3, 6, 9, 12, ..., 36.
17
Die eben aufgeführten Wettmöglichkeiten beziehen sich auf die Anordnung im Tableau. In
manchen Casinos ist es auch möglich, so genannte Kesselspiele zu spielen. Hierbei wird die
Anordnung der Zahlen im Rouletterad als Grundlage für die Wettmöglichkeiten genommen.
Da alle Fälle auch auf die bereits erwähnten Wettmöglichkeiten übertragbar sind, werden diese im weiteren Verlauf der Arbeit nicht mehr behandelt. In der nachfolgenden Grafik sind die
Setzmöglichkeiten auf dem Tableau veranschaulicht:
Abbildung 1: Setzmöglichkeiten auf dem Tableau
III.2 Der Vorteil der Bank
Nachdem nun alle Wettmöglichkeiten bekannt sind, interessiert uns natürlich auch hier, genau
wie beim Chuck-a-Luck, ob die Bank im Vorteil ist und wenn ja wie stark. Wir gehen im Folgenden davon aus, dass alle Zahlen bzw. Ereignisse mit gleicher Wahrscheinlichkeit auftreten,
d. h. es gibt keine Unregelmäßigkeiten auf Grund von Fehlern im Rouletterad oder sonstigen
äußeren Einflüssen. Wir betrachten also einen Laplace-Raum mit 37 bzw. 38 Ereignissen. Um
die einzelnen Erwartungswerte der Wettmöglichkeiten berechnen zu können, muss man zunächst wissen, wie die Auszahlung der Bank für den Fall aussieht, dass die Kugel auf die Null
bzw. die Doppel-Null fällt.
18
Beim Französischen Roulette verliert der Spieler seinen kompletten Einsatz, wenn er auf
Mehrfachchancen gesetzt hat. Ausnahmen sind hierbei natürlich alle Fälle, bei denen der
Spieler auf die Null gesetzt hat. Dies ist bei den Spielmöglichkeiten Plein, Cheval und natürlich Carré (Les quatre premiers) möglich.
Fällt die Kugel auf die Null, wenn der Spieler auf eine einfache Chance setzt, wird sein Einsatz gesperrt. Der Einsatz ist wieder frei, wenn im nächsten Spiel die Kugel auf die vom Spieler gesetzte einfache Chance fällt. Ist dies nicht der Fall, hat der Spieler seinen Einsatz verloren. Sollte die Kugel beim zweiten Mal wieder auf die Null fallen, ist der Einsatz doppelt gesperrt. Im relativ unwahrscheinlichen Fall, dass die Kugel dreimal in Folge auf die Null fällt,
verliert der Spieler seinen Einsatz.
Der Spieler hat auch die Möglichkeit, sich die Hälfte seines Einsatzes auszahlen zu lassen
oder seinen gesperrten Einsatz auf eine andere einfache Chance zu verschieben, wenn die
Kugel das erste Mal auf die Null gefallen ist.
Beim Amerikanischen Roulette, wie es in europäischen Casinos angeboten wird (mit den Zahlen 0 und 1 – 36), bekommt der Spieler, wenn er auf einfache Chancen setzt, die Hälfte seines
Einsatzes ausgezahlt, wenn die Kugel auf die Null fällt. Die Regel, dass der Einsatz gesperrt
wird, gibt es hier nicht.
In den USA verliert der Spieler beim Amerikanischen Roulette (mit den Zahlen 0, 00 und 1 –
36), das als einziges angeboten wird, seinen kompletten Einsatz, wenn die Kugel auf die Null
oder die Doppel-Null fällt.
Nachdem die Auszahlung für den Fall der Null (Doppel-Null) erläutert wurde, ist klar, dass
sich die Bank durch die Null (Doppel-Null) einen Vorteil gegenüber dem Spieler sichert, denn
ohne die Null (Doppel-Null) gleichen sich Einsatz und Gewinn bei allen Wettmöglichkeiten
aus. Wie stark dieser Vorteil für die einzelnen Varianten ist, wird nun aufgezeigt.
Beim Französischen Roulette beträgt der Vorteil der Bank bei den einfachen Chancen
1 18
1 1 18
1 1 1
· +
·
· +
· ·
= 0,01352 = 1,352 %.
37 37 37 37 37 37 37 37
Dabei gehen wir davon aus, dass sich der Spieler nicht dafür entscheidet, sich die Hälfte seines Einsatzes auszahlen zu lassen, nachdem das erste Mal die Kugel auf die Null gefallen ist.
Für die mehrfachen Chancen liegt der Vorteil beim Französischen Roulette bei
1
= 0,02703 = 2,703 %.
37
19
Beim Amerikanischen Roulette, wie es in europäischen Casinos angeboten wird, beträgt der
Vorteil der Bank bei den einfachen Chancen
1 18
· = 0,1315 = 1,315 %.
37 37
Dieser etwas geringere Vorteil der Bank ist auch beim Französischen Roulette erreichbar,
wenn sich der Spieler dafür entscheidet, sich die Hälfte seines Einsatzes auszahlen zu lassen,
nachdem die Kugel das erste Mal auf die Null gefallen ist.
Für die mehrfachen Chancen entspricht der Vorteil der Bank dem des Französischen Roulettes.
Und zuletzt der Vorteil der Bank beim Amerikanischen Roulette wie es in den USA angeboten wird. Dieser beträgt für die einfachen, wie auch für die mehrfachen Chancen
2
= 0,05263 = 5,263 %.
38
In der nachfolgenden Tabelle sind fürs Französische Roulette die Gewinnquote, die Gewinnwahrscheinlichkeit und der Erwartungswert mit der dazugehörigen Varianz und Standardabweichung für die einzelnen Wettarten zusammengefasst. Dabei gehen wir wieder davon aus,
dass der Spieler sich nicht die Hälfte des Gewinns auszahlen lässt, wenn die Kugel auf die
Null fällt.
Gewinnquote
Gewinnwahrscheinlichkeit
Erwartungswert
Varianz
Standardabweichung
Rouge/Noir
1 zu 1
49,324%
0,9865
0,9998
0,9999
Pair/Impair
1 zu 1
49,324%
0,9865
0,9998
0,9999
Manque/Passe
1 zu 1
49,324%
0,9865
0,9998
0,9999
Douzaine
2 zu 1
12/37 = 32,433%
0,9730
1,9722
1,4044
Colonne
2 zu 1
12/37 = 32,433%
0,9730
1,9722
1,4044
Transversale Simple
5 zu 1
6/37 = 16,216%
0,9730
4,8912
2,2116
Carré
8 zu 1
4/37 = 10,811%
0,9730
7,8101
2,7947
Transversale Pleine
11 zu 1
3/37 = 8,108%
0,9730
10,7290
3,2755
Cheval
17 zu 1
2/37 = 5,405%
0,9730
16,5668
4,0702
Plein
35 zu 1
1/37 = 2,703%
0,9730
34,0804
5,8378
Wettart
Tabelle 4: Französisches Roulette
Zusammenfassend können wir sagen, dass der Spieler beim Französischen Roulette durchschnittlich pro Spiel mindestens 1,315 % seines Einsatzes verliert und der Erwartungswert
dementsprechend maximal bei 0,98685 Einsätzen liegt. Außerdem ist es für den Spieler vorteilhafter, auf Wettmöglichkeiten mit einfachen Gewinnchancen zu setzen. Bei den mehrfa20
chen Chancen ist es logischerweise so, dass mit sinkender Gewinnwahrscheinlichkeit das Risiko, d. h. die Varianz, steigt. Des Weiteren können wir festhalten, dass der Erwartungswert
des Spielers bei den Varianten, die in europäischen Casinos angeboten werden, deutlich größer ist, als bei der, die in amerikanischen Casinos angeboten wird.
III.3 Spielsysteme
Seitdem es Glücksspiele gibt, wird nach unfehlbaren Gewinnsystemen gesucht. Das heißt
Systeme, bei denen der Spieler einen positiven Erwartungswert hat. Wie bei allen Casinospielen wurde auch fürs Roulette eine Vielzahl von Systemen entwickelt, die dem Spieler den
erhofften Gewinn garantieren sollten. Diese Suche nach dem unfehlbaren System fürs Roulette war allerdings erfolglos und wird es auch immer bleiben. Im Gegensatz zum Black-Jack,
das unter bestimmten Spielregeln bereits geknackt wurde (vgl. hierzu Bewersdorff (2007), S.
88 f.), ist das Roulette ein leichter überschaubares Spiel, dessen Erwartungswert nicht verbesserbar ist.
Im weiteren Verlauf der Arbeit soll beispielhaft ein Spielsystem vorgestellt und auf seine Vorund Nachteile überprüft werden. Die bekanntesten Spielsysteme fürs Roulette sind die so genannten Martingale-Strategien, bei denen mit variablen Einsätzen operiert wird. Bei den Martingale-Strategien setzt der Spieler ausschließlich auf einfache Chancen und erhöht seinen
Einsatz im Verlustfall. Martingale-Spielstrategien sind zum Beispiel die „Martingale classique“, die Montante Américaine, die Montante Hollandaise und die Progression d’Alembert.
III.3.1 Die „Martingale classique“
Die „Martingale classique“ ist die Strategie des Verdoppelns (Doublieren). Sie ist die wohl
bekannteste Spielstrategie fürs Roulette. Der Spieler startet dabei mit einem Einsatz. Im Verlustfall verdoppelt er seinen Einsatz solange, bis er gewinnt. Wenn er das erste Mal gewinnt,
hat er insgesamt einen Einsatz Gewinn gemacht und startet die nächste Runde wieder mit einem Einsatz.
Bei diesem System ist es relativ wahrscheinlich, einen kleinen Gewinn zu verzeichnen. Nicht
zu unterschätzen ist allerdings auch das Risiko eines großen Verlustes, denn zum Beispiel
nach bereits vier verlorenen Spielen in Folge beträgt die Höhe des nächsten Einsatzes das 16fache des Anfangseinsatzes. Kann man diesen Einsatz nicht mehr aufbringen, hat man in die-
21
ser Runde 15 Einsätze verloren. Wir sehen, wie schnell es passieren kann, dass man sein
komplettes Budget verspielt.
In Casinos ist es üblich, dass es einen Höchsteinsatz gibt. Dieser richtet sich nach dem Mindesteinsatz. Oft beträgt der Höchsteinsatz das 1200-fache des Mindesteinsatzes. Unter diesen
Bedingungen wäre die elfte Verdopplung bei der Spielstrategie „Martingale classique“ nicht
mehr erlaubt.
Im weiteren Verlauf der Arbeit sollen einige Spielwahrscheinlichkeiten für die Spielstrategie
„Martingale classique“ berechnet werden. Dazu müssen allerdings zunächst einige neue Begriffe eingeführt werden.
III.4 Bernoulli-Experimente
Bernoulli-Experimente sind Experimente, die nur zwei mögliche Ergebnisse haben. Sie sind
nach dem Schweizer Mathematiker Jakob Bernoulli (1654 – 1705) benannt. Die zwei möglichen Ergebnisse werden in der Regel mit Erfolg (E) und Misserfolg (M) bezeichnet. Wir bezeichnen die Wahrscheinlichkeit für einen Erfolg mit p und die Wahrscheinlichkeit für einen
Misserfolg mit q = 1 – p. Wir führen im Folgenden drei diskrete Verteilungen ein, die hilfreich bei der Analyse des Roulettes sind.
Definition:
Eine Zufallsvariable X heißt diskret, wenn es eine endliche oder abzählbar
unendliche Teilmenge D C R gibt mit P(X " D) = 1.
Definition:
(Bernoulli-Verteilung) Wir definieren die Zufallsvariablen Xi, i = 1, …, n,
!
durch
1 für ωi = E
Xi(ω) =
0 für ωi = M
{
Dabei gibt Xi an, ob das i-te Experiment ein Erfolg oder ein Misserfolg ist. Die
Wahrscheinlichkeitsfunktion dieser Zufallsvariablen lautet
{
p(k) =
1 – p für k = 0
p
für k = 1
Die zugehörige Verteilung auf {0, 1} heißt Bernoulli-Verteilung mit Parameter
p, kurz Bernoulli(p)-Verteilung. Die geschlossene Darstellung der Wahrscheinlichkeitsfunktion lautet:
22
p(k) = pk(1 – p)1–k,
k " {0, 1}.
Eine Bernoulli(p)-verteilte Zufallsvariable, d.h. P(X = 1) = p und P(X = 0) = 1 – p, hat den
!
Erwartungswert
E(X) = 0 · (1 – p) + 1 · p = p
und die Varianz
Var(X) = p – p2 = p(1 – p) = pq.
Definition:
(Binomiale Verteilung) Wir definieren die Zufallsvariable Sn durch
Sn := X1 + … + Xn.
Sn gibt die Anzahl der Erfolge in n Experimenten an. Die Wahrscheinlichkeitsfunktion, die die Wahrscheinlichkeit für k Erfolge angibt, lautet
&n#
p(k) = P(Sn = k) = $$ !! pk · (1 – p)n–k
%k "
für k = 0, …, n.
Die zugehörige Verteilung auf {0, …, n} heißt binomiale Verteilung mit Parametern n und p, kurz Bin(n, p)-Verteilung.
Der Erwartungswert einer Bin(n, p)-Verteilung lautet
E(X)
n
!
=
k =o
n
n ' 1# k
n &$
p (1 – p)n–k
$ k ' 1!!
%
"
!
=
k =1
n
= np
!
k =1
& n ' 1# pk–1 (1 – p)(n–1) – (k–1)
$$
!!
% k ' 1"
n "1
= np
&n# k
n–k
k $$ !! p (1 – p)
%k "
!
l =0
& n ' 1# p l (1 – p) (n !1)!l
$$
!!
% l "
= np.
&n#
& n ' 1#
!! . Des Weiteren haben wir auch die NewHierbei wurde benutzt, dass gilt: k $$ !! = n $$
%k "
% k ' 1"
ton’sche Binomialformel mit x = p, y = 1 – p und n – 1 angewendet.
23
Die Varianz lautet
Var(X)
= E(X2) – (E(X))2
= E(X(X – 1)) + E(X) – (E(X))2
n
=
n
k (k – 1) &$ #! pk (1 – p)n–k + np – (np)2
$k !
% "
!
k =o
n
= n(n – 1)p2
& n ' 2 # pk–2 (1 – p)(n–2) – (k–2) + np – (np)2
$$
!!
% k ' 2"
!
k =2
= n(n – 1)p2 + np – (np)2 = np – np2 = np(1 – p)
= npq.
Mit Hilfe der binomialen Verteilung können wir zum Beispiel die Wahrscheinlichkeit berechen, dass unter n unabhängigen Roulettespielen k Erfolge auftreten. Die Wahrscheinlichkeit
p für die entsprechende Spielstrategie können wir aus Tabelle 4 entnehmen.
Definition:
(Geometrische Verteilung) Für eine unendliche Folge unabhängiger BernoulliExperimente definieren wir eine Zufallsvariable T, die die Anzahl der Misserfolge vor dem ersten Erfolg angibt. T ist eine diskrete Zufallsvariable mit Wertebereich {0, 1, …}. Falls p > 0 ist, hat T die Wahrscheinlichkeitsfunktion
p(k) = P(T = k) = P(X1 = … = Xk = 0, Xk+1 = 1)
= (1 – p)k · p.
Die Verteilung heißt geometrische Verteilung auf N0 mit Parameter p.
Satz: Für geometrisch verteilte Zufallsvariablen gilt
P(T ≥ k)
"
=
!
"
j
(1 – p) p = (1 – p) p
k
j =k
!
j =0
= qkp
1
= qk.
1 ! (1 ! p )
24
pj
Der Erwartungswert einer geometrisch verteilten Zufallsvariable lautet
E(X)
"
=
"
k
!
kq p = pq
k =0
kqk–1
!
k =0
1
= pq
(1 ! q )2
=
q
.
p
Die Varianz einer geometrisch verteilten Zufallsvariable lautet
Var(X)
= E(X2) – (E(X))2
= E(X(X – 1)) + E(X) – (E(X))2
"
q q2
k
k(k – 1)q p + – 2
p p
!
=
k =0
"
k–2
!
k(k – 1)q
= pq2
2
2
= pq
+
k =2
=
(1 ! q )3
+
q q2
–
p p2
q q2
–
p p2
q
2q 2 q q 2
+ – 2 = 2 (q + p)
2
p p
p
p
=
q
.
p2
Dabei haben wir für die Berechnung des Erwartungswertes und der Varianz benutzt, dass für
│x│< 1 und r = 1, 2, … gilt:
1
(1 ! x )r
"
=
!
k =0
& k + r ' 1# k =
$$
!! x
% k "
"
!
k =0
& k + r ' 1# k
$$
!! x .
% r '1 "
Den Beweis hierzu finden wir in dem Buch „Einführung in die Wahrscheinlichkeitstheorie
und Statistik“ (2004, S. 73 f.) von Herold Dehling.
Nachdem nun die für uns wichtigsten Verteilungen und die dazugehörigen Erwartungswerte
bekannt sind, können wir die „Martingale classique“ genauer untersuchen.
25
III.5 Gewinnerwartung der „Martingale classique“
Bei der von uns betrachteten Version des Französischen Roulettes liegt die Erfolgswahrscheinlichkeit p bei p = 0,49324 und die Misserfolgswahrscheinlichkeit q bei q = 0,50676.
Einem einzigen Roulettespiel liegt also ein Bernoulli-Experiment zu Grunde.
Für uns viel wichtiger ist aber die Feststellung, dass wir bei der Spielstrategie „Martingale
classique“ eine geometrisch verteilte Zufallsvariable mit dem eben genannten Parameter p =
0,49324 betrachten können. Denn bei der „Martingale classique“ spielt der Spieler solange
weiter, bis er den ersten Erfolg verzeichnet. In der nachfolgenden Tabelle sind die einzelnen
Wahrscheinlichkeiten aufgelistet, dass der Spieler in Runde k den ersten Erfolg verzeichnet.
Hierbei wird wieder von einem Höchsteinsatz ausgegangen, der das 1200-fache des Mindesteinsatzes beträgt. Dementsprechend kann in Runde k = 12 nicht mehr verdoppelt werden.
Deshalb wird in dieser Zeile die Wahrscheinlichkeit P(T ≥ k) aufgeführt, die für den Verlust
von 2047 Einheiten steht. Wir wissen aus dem letzten Satz, dass diese Wahrscheinlichkeit mit
der Formel
P(T ≥ k) = qk
berechnet werden kann.
Runde (k)
Anzahl der
Einsätze
Wahrscheinlickeit auf
Erfolg in Runde k
(gerundete Werte)
1
1
0,493
2
2
0,507 _0,493 = 0,250
3
4
(0,507) 2 _0,493 = 0,127
4
8
3
(0,507) _0,493 = 0,064
5
16
(0,507) 4 _0,493 = 0,033
6
32
5
(0,507) _0,493 = 0,016
7
64
(0,507) 6_0,493 = 0,835_10 -2
8
128
7
-2
(0,507) _0,493 = 0,423_10
9
256
(0,507) 8_0,493 = 0,215_10 -2
10
512
9
-2
(0,507) _0,493 = 0,109_10
11
1024
(0,507) 10 _0,493 = 0,551_10 -3
!12
_
(0,507)
26
11
-3
= 0,566_10
Tabelle 5: Wahrscheinlichkeit auf Erfolg in Runde k mit der Spielstrategie „Martingale classique“
Wie bereits erwähnt wurde, bietet die Spielstrategie „Martingale classique“ eine relativ hohe
Wahrscheinlichkeit auf einen kleinen Gewinn. Die Verlustwahrscheinlichkeit liegt bei
r = 0,566·10-3, wenn man ein Budget von 2047 Einheiten zur Verfügung hat. Dieser Verlust
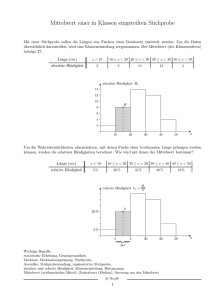
beträgt allerdings auch das komplette Budget. Das folgende Diagramm soll die Wahrscheinlichkeit aufzeigen, dass man einen Gewinn von G ≥ g erzielt. Dabei ist G eine diskrete Zufallsvariable, die geometrisch mit Parameter r = 0,566·10-3 verteilt ist. Hierbei möchten wir
auf eine Besonderheit in der Notation hinweisen. Üblicherweise werden bei der geometrischen Verteilung die Misserfolge vor dem ersten Erfolg gezählt. In diesem Fall warten wir auf
den Verlustfall, der nach unserer Definition für einen Erfolg steht. Für die Berechnung der
Wahrscheinlichkeit, dass G ≥ g ist, stellt dies natürlich kein Problem dar. Diese Wahrscheinlichkeit wird mit der Formel
P(G ≥ g) = sg
berechnet. Dabei ist s = 1 – r = 0,99943.
P(G!g)
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
500
1000
1500
2000
g
Grafik 1: Wahrscheinlichkeit, einen Gewinn größer g zu erzielen
27
2500
3000
Wir sehen, dass man ungefähr jedes zweite Mal mehr als 1225 Einheiten gewinnt. Dies gilt
natürlich nur, wenn man sich an dieser Stelle dazu entscheidet, nicht weiter zu spielen. Denn
in jeder Runde droht der Verlust von 2047 Einheiten. Den besten Überblick über die Spielstrategie gibt der Erwartungswert. Dieser lautet:
E(X) = s · 2 – r · 2047 = 0,8402.
Der Erwartungswert mit der Spielstrategie „Martingale classique“ ist also deutlich schlechter
als der eines einzelnen Spiels. Durchschnittlich verliert man fast 16% seines Einsatzes.
28
IV. Literaturverzeichnis
Bewersdorff, J. (2007). Glück, Logik und Bluff: Mathematik im Spiel: Methoden, Ergebnisse
und Grenzen. 4., durchges. und erg. Auflage. Wiesbaden: Vieweg.
Dehling, H. & Haupt, B. (2004). Einführung in die Wahrscheinlichkeitstheorie und Statistik. 2.
Auflage. Berlin [u. a.]: Springer-Verlag.
http://www.istockphoto.com/file_thumbview_approve/1374122/2/istockphoto_1374122_roul
ette.jpg (16.03.2008).
http://de.wikipedia.org/wiki/Roulette_(Gl%C3%BCcksspiel) (16.03.2008).
http://www.westspiel.de/content/de/westspiel/03_spielinfo/002_klassisches_spiel/001_roulett
e.php (16.03.2008).
29