Berechnen von Winkeln zwischen zwei Vektoren: Skalarprodukt

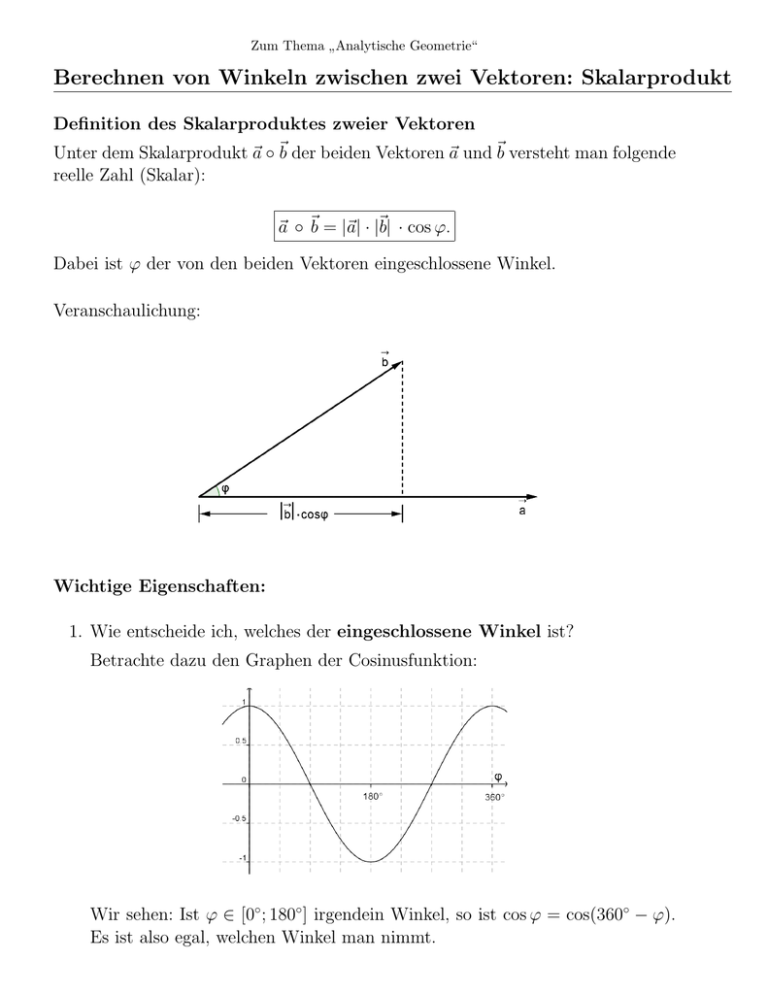
Zum Thema Analytische Geometrie“
”
Berechnen von Winkeln zwischen zwei Vektoren: Skalarprodukt
Definition des Skalarproduktes zweier Vektoren
Unter dem Skalarprodukt ~a ◦ ~b der beiden Vektoren ~a und ~b versteht man folgende
reelle Zahl (Skalar):
~a ◦ ~b = |~a| · |~b| · cos ϕ.
Dabei ist ϕ der von den beiden Vektoren eingeschlossene Winkel.
Veranschaulichung:
Wichtige Eigenschaften:
1. Wie entscheide ich, welches der eingeschlossene Winkel ist?
Betrachte dazu den Graphen der Cosinusfunktion:
Wir sehen: Ist ϕ ∈ [0◦ ; 180◦ ] irgendein Winkel, so ist cos ϕ = cos(360◦ − ϕ).
Es ist also egal, welchen Winkel man nimmt.
2. Es gilt das Kommutativgesetz:
~a ◦ ~b = ~b ◦ ~a.
Beweis: ~a ◦ ~b = |~a| · |~b| · cos ϕ = |~b| · |~a| · cos ϕ = ~b ◦ ~a.
3. Reelle Zahlen dürfen wir rausziehen“:
”
(λ · ~a) ◦ ~b = λ · (~a ◦ ~b) = ~a ◦ (λ · ~b);
λ ∈ R.
Beweis: (λ · ~a) ◦ ~b = |λ · ~a| · ~b · cos ϕ = |λ| · |~a| · |~b| · cos ϕ.
4. Es gilt das Distributivgesetz:
~a ◦ (~b + ~c) = ~a ◦ ~b + ~a ◦ ~b.
Beweis: Nur für den Spezialfall, dass ~a, ~b und ~c komplanar sind (d. h. in einer
Ebene liegen):
Wie können wir nun mit Hilfe des Skalarproduktes den Innenwinkel
zwischen zwei Vektoren ausrechnen?
Seien


a1
~a =  a2 
a3


b1
und ~b =  b2  .
b3
Wir schreiben nun


 
 
1
0
0
~a = a1 ·  0  + a2 ·  1  + a3 ·  0  .
0
0
1
Um nicht so viel schreiben zu müssen, nennen wir die Einheitsvektoren“
”
 
 
 
0
0
1





~e1 = 0 , ~e2 = 1 , ~e3 = 0  .
0
1
0
Damit ist
~a ◦ ~b = (a1 · ~e1 + a2 · ~e2 + a3 · ~e3 ) ◦ (b1 · ~e1 + b2 · ~e2 + b3 · ~e3 ).
Wenden wir die Rechenregeln 2., 3. und 4. mehrfach an, so erhalten wir
~a ◦ ~b = a1 b1 · ~e1 ◦ ~e1 + a2 b2 · ~e2 ◦ ~e2 + a3 b3 · ~e3 ◦ ~e3
+(a1 b2 + a2 b1 ) · ~e1 ◦ e~2 + (a1 b3 + a3 b1 ) · ~e1 ◦ e~3 + (a2 b3 + a3 b2 ) · ~e2 ◦ e~3 .
Im Kartesischen Koordinatensystem stehen die Vektoren ~e1 , ~e2 und ~e3 alle senkrecht aufeinander und haben die Länge 1. Das macht das Ganze viel einfacher,
denn wir erhalten somit:
~a ◦ ~b = a1 b1 + a2 b2 + a3 b3 .
Berechnen von Winkeln zwischen zwei Vektoren
Wir haben
~a ◦ ~b = |~a| · |~b| · cos ϕ
und
~a ◦ ~b = a1 b1 + a2 b2 + a3 b3 .
Also gilt:
|~a| · |~b| · cos ϕ = a1 b1 + a2 b2 + a3 b3
und somit für den Cosinus des Winkels zwischen ~a und ~b:
cos ϕ =
bzw. mit den Längen der Vektoren:
a1 b 1 + a2 b 2 + a3 b 3
|~a| · |~b|
cos ϕ = p
a1 b 1 + a2 b 2 + a3 b 3
p
.
2
2
2
a1 + a2 + a3 · b21 + b22 + b23
Beispiel:
In einem kartesischen KOSY legen die Punkte A(1|4|0), B(3|2|0) und C(−2|−5|0)
ein Dreieck in einer Ebene fest. Berechne den Innenwinkel zwischen den Strecken
[AB] und [AC].
Lösung:

   
2
1
3
−→ −−→ −→     
AB = OB − OA = 2 − 4 = −2 
0
0
0

   

−3
1
−2
−→ −→ −→ 
AC = OC − OA = −5  −  4  =  −9 
0
0
0

−→ −→
AB ◦ AC
2 · (−3) + (−2) · (−9) + 0 · 0
p
cos ϕ = −→ −→ = p
≈ 0, 447
2
2
2
2 + (−2) + 0 · (−3)2 + (−9)2 + 02
AB · AC Daraus folgt:
ϕ = cos−1 (0, 447) ≈ 63, 4