1.Besondere Produkte von Vektoren

1.Besondere Produkte von Vektoren
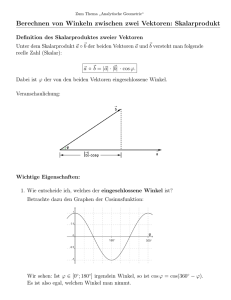
1.1 Skalarprodukt zweier Vektoren
Beispiel: Physikà Definition der mechanischen Arbeit : W = F • s = F s cos( ∠F, s)
W…skalare Größe F, s vektorielle Größen
W = F s à F // s
1.1.1 Definition:
(zur besseren Verständigung: • Multiplikation von Vektoren)
Das Skalarprodukt a • b zweier Vektoren a und b
ist die reelle Zahl a • b = a b cos ∠(a, b) , wobei ∠(a,b) einer der beiden Winkel ist,
die von beiden Vektoren eingeschlossen werden.
Bsp. a = a = 3,5 b = b = 3 und ∠(a,b) =
= 120 °
à a • b = a ⋅ b ⋅ cos ∠(a,b) = 3,5 ⋅ 3 ⋅ cos120° = -5,25
ϕ
a • b = a ⋅ b ⋅ cos
a •b = a ⋅b
a•b > 0
a•b = 0
a •b< 0
a •b= - a ⋅b
0°
0° < ϕ < 90°
ϕ = 90°
90° < ϕ < 180°
ϕ = 180°
1.1.2 Anwendungen:
a) Zueinander senkrechte (orthogonale) Vektoren
Zwei Vektoren a, b ≠ 0 stehen genau senkrecht, wenn ihr Skalarprodukt gleich Null
ist à a ⊥ b ⇔ a • b = 0
b) Betrag eines Vektors
a • a = a ⋅ a ⋅ cos 0° = a 2
a = a•a = a
2
c) Einheitsvektoren à haben den Betrag 1.
Zu jedem Vektor a ≠ 0 gibt es einen gleichgerichteten Einheitsvektor a 0
1
mit a 0 = ⋅ a
a
d) Winkel zwischen zwei Vektoren
cos∠(a.b) =
a•b
= a0 • b0
a ⋅b
e) Rechengesetze für das Skalarprodukt
(1) a • b = b • a
(2) ( a + b) • c = a • c + b • c
(3) ( λa) • b = λ(a • b)
1
1.1.3 Das Skalarprodukt in Koordinatenschreibweise
{
}
Sei u1,u2 ,(u3 ) eine Basis des zwei- bzw. dreidimensionalen Vektorraumes und
bzw. b = b1 u1 + b 2 u 2 + b 3 u 3
a = a 1 u1 + a 2 u 2 + a 3 u 3
dann a • b = a1b1 ⋅ (u1 • u1 ) + a1b 2 (u1 • u 2 ) + a1b 3 (u1 • u 3 )
+ a 2b1 ⋅ (u 2 • u1 ) + a 2b 2 (u 2 • u 2 ) + a 2b 3 (u 2 • u 3 )
+ a 3 b1 ⋅ (u 3 • u1 ) + a 3 b 2 (u 3 • u 2 ) + a 3 b 3 (u 3 • u 3 )
Definition: orthonormierte Basis
Eine Basis e1, e 2 , (e 3 ) heißt orthonormiert, wenn:
{
}
(1) die Länge jedes Basisvektors 1 ist d. h. ei • ei = 1 ( i = 1,2,3)
(2) die Basisvektoren aufeinander senkrecht stehen d. h. ei • e j = 0
(1 ≤ i, j ≤ 3, i ≠ j )
Bzgl. einer orthonormierten Basis lautet das Skalarprodukt zweier Vektoren in
Koordinatenschreibweise:
⎛ a1 ⎞ ⎛ b1 ⎞
⎜ ⎟ ⎜ ⎟
a • b = ⎜ a 2 ⎟ • ⎜ b 2 ⎟ = a1 ⋅ b1 + a 2 ⋅ b 2 + a 3 ⋅ b 3
⎜ a ⎟ ⎜ b ⎟
⎝ 3 ⎠ ⎝ 3 ⎠
1.1.4 Anwendungen: bzgl. einer orthonormierten Basis gilt:
a) a ⊥ b ↔ a1b1 + a 2 b 2 + a 3 b 3 = 0
2
2
b) a = a1 + a 2 + a 3
2
1
1
c) a 0 = a =
2
2
2
a
a1 + a 2 + a 3
d) cos ∠(a, b) =
⎛ a1 ⎞
⎜ ⎟
⎜ a 2 ⎟
⎜ a ⎟
⎝ 3 ⎠
⎛ 2 ⎞
⎜ ⎟
Bsp. a = ⎜ − 2 ⎟ → a 0 =
⎜ 1 ⎟
⎝ ⎠
⎛ 2 ⎞
⎜
⎟
⎛ 2 ⎞ ⎜ 3 ⎟
⎜ ⎟ ⎜ − 2 ⎟
1
⎜ − 2 ⎟ =
4 + 4 + 1 ⎜ ⎟ ⎜ 3 ⎟
⎝ 1 ⎠ ⎜ 1 ⎟
⎜
⎟
⎝ 3 ⎠
a1b1 + a 2 b 2 + a 3 b 3
a•b
= a0 • b0 =
2
2
2
2
2
2
a⋅b
a1 + a 2 + a 3 b1 + b 2 + b 3
⎛ 2 ⎞
⎛ 3 ⎞
⎜ ⎟
⎜ ⎟
Bsp. a = ⎜ 0 ⎟ b = ⎜ 0 ⎟ bzgl. ONB à
⎜ 1 ⎟
⎜ − 1⎟
⎝ ⎠
⎝ ⎠
2 ⋅ 3 + 0 ⋅ 0 + 1⋅ ( −1)
1
cos ∠ a, b =
=
→ ∠(a, b) = 45 °
2
2
2
2
2
2
2
2 + 0 + 1 ⋅ 3 + 0 + ( −1)
( )
2
1.1.5 Messung im kartesischen Koordinatensystem
à Ein Koordinatensystem mit einer ONB heißt
kartesischen Koordinatensystem.
Anwendungen :
a) Länge einer Strecke
Sind A( a1/ a2/ a3 ) bzw. B( b1/ b2/ b3 )Punkte in einem kartesischen
Koordinatensystem dann AB = AB =
(b1 − a1 )2 + (b 2 − a 2 )2 + (b3 − a3 )2
2
2
Bsp.: A (1/2/ -3) B (3/ -2/-1) à AB = (3 − 1)2 + (− 2 − 2) + (− 1 + 3) = 2 6
b) Innenwinkel eines Dreiecks
Sind A( a1/ a2/ a3 ), B( b1/ b2/ b3 ) und C( c1 /c2 / c3 ) Eckpunkte eines Dreiecks in
einem kartesischen Koordinatensystem, dann gilt z.B. für den Innenwinkel γ :
cos γ =
CA • CB
CA ⋅ CB
Bsp.: A(0/2/0), B(0/-6/0), C( (0/0/2)
⎛ 0 ⎞
⎛ 0 ⎞
⎜ ⎟
⎜ ⎟
à CA = ⎜ 2 ⎟ CB = ⎜ − 6 ⎟ à CA • CB = −8
⎜ − 2 ⎟
⎜ − 2 ⎟
⎝ ⎠
⎝ ⎠
−8
à γ ≈ 116,57 °
CA = 8 CB = 40 à cos γ =
8 40
c) Schnittwinkel zweier Geraden
Sind g: x = a + λv und h: x = b + µu
Geraden in einem kartesischen Koordinatensystem, dann gilt für den
Schnittwinkel ∠ (g,h):
cos ∠(g, h) =
u•v
u⋅v
⎛ 1 ⎞ ⎛ 1 ⎞
⎛ 1 ⎞ ⎛ 3 ⎞
⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟
Bsp. g: x = ⎜ 0 ⎟ + λ⎜ 2 ⎟ h: x = ⎜ 0 ⎟ + µ⎜ 0 ⎟
⎜ 0 ⎟ ⎜ 1 ⎟
⎜ 0 ⎟ ⎜ − 5 ⎟
⎝ ⎠ ⎝ ⎠
⎝ ⎠ ⎝ ⎠
cos(∠g, h) =
−2
→ ∠(g, h) ≈ 83,37°
30 10
d) Winkelhalbierende
Sind g: x = a + λv und h: x = b + µu zwei sich schneidende
Geraden und ist s der Ortsvektor des Schnittpunktes, dann
lauten die Gleichungen der Winkelhalbierenden
w: x = s + λ(v 0 ± u0 )
3