statistik_Okt_18_05

STATISIK
LV Nr.: 0021
WS 2005/06
18. Oktober 2005
1
Zweidimensionale Merkmale
• Frage: Wie lässt sich der Zusammenhang
bzw. die Abhängigkeit zw. zwei Merkmalen
messen?
– Wie stark ist der Zusammenhang bzw. die
Abhängigkeit?
Antwort durch Korrelationsrechnung.
– Lässt sich der Zusammenhang in einer
bestimmten Form darstellen?
Antwort durch Regressionsrechnung.
2
Zweidimensionale Merkmale
• n Untersuchungseinheiten, 2 Merkmale X
und Y, Ausprägungen des Merkmals X
a1,…,al und Ausprägungen des Merkmals Y
b1,…,bm.
• 2-dimensionales Merkmal (X,Y) mit
Ausprägungen (aj,bk), mit absoluten
Häufigkeiten hjk und relativen Häufigkeiten
fjk=1/n·hjk
3
Kontingenztafel
• Häufigkeitsverteilung von (X,Y) wird durch
Kontingenztafel dargestellt.
X
Y b1
a1
h11
:
:
al
hl1
…
bm
…
h1m
:
…
hlm
4
Kontingenztafel
• Bsp. Geschlecht (X) Rauchverhalten (Y):
absolute und relative Häufigkeiten von
(X,Y).
X
Y R
N-R
X
Y R
N-R
w
9
32
w
0,12
0,44
m
5
27
m
0,07
0,37
5
Kontingenztafel
• Absolute Randhäufigkeiten
– von aj für j=1,…,l und bk für k=1,...,m:
m
h j   h jk
k 1
l
h k   h jk
j1
• Relative Randhäufigkeiten
– von aj für j=1,…,l und bk für k=1,…,m:
m
f j   f jk
k 1
l
f k   f jk
j1
• Randhäufigkeiten ergeben die Häufigkeitsverteilung des Merkmals X bzw.Y
(Randverteilung).
6
Kontingenztafel
• Kontingenztafel absoluten Häufigkeiten und
Randhäufigkeiten
X
Y b1
…
bm
Σ
…
h1m
h1.
:
:
a1
h11
:
:
al
hl1
…
hlm
hl.
Σ
h.1
…
h.m
h..=n
7
Kontingenztafel
• Kontingenztafel relative Häufigkeiten und
Randhäufigkeiten
X
Y b1
…
bm
Σ
a1
f11
…
f1m
f1.
:
:
:
:
al
fl1
…
flm
fl.
Σ
f.1
…
f.m
f..=1
8
Kontingenztafel
Es gilt:
• Relative Randhäufigkeit = 1 / n · absolute
Randhäufigkeit
1
1
f j  h j und f k  h k
n
n
• Summe der absoluten Randhäufigkeiten = n
l
m
 h
j1 k 1
jk
l
m
j1
k 1
l
m
j1
k 1
  h j  h k  n
• Summe der relativen Randhäufigkeiten = 1
l
m
 f
j1 k 1
jk
  f j  fk  1
9
Kontingenztafel
• Bsp. Geschlecht (X) Rauchverhalten (Y):
absolute und relative Häufigkeiten und
Randhäufigkeiten von (X,Y).
R
N-R

X
w
9
32
41
w
0,12
0,44 0,56
m
5
27
32
m
0,07
0,37 0,44

14
59
73

0,19 0,81
X
Y
Y
R
N-R

1
10
Kontingenztafel
• Bsp. Geschlecht (X) Rauchverhalten (Y):
• Zeilenprozent:
R
N-R

X
w
9
32
41
m
5
27

14
59
X
Y
R
N-R

w
0,22
0,78
1
32
m
0,16
0,84
1
73

0,19 0,81
1
Y
11
Kontingenztafel
• Bsp. Geschlecht (X) Rauchverhalten (Y):
• Spaltenprozent:
R
N-R

X
w
9
32
41
w
0,64
0,54 0,56
m
5
27
32
m
0,36
0,46 0,44

14
59
73

1
X
Y
Y
R
N-R
1

1
12
Darstellung
Geschlecht - Rauchverhalten
1
0,9
0,8
0,7
0,6
0,78
0,84
0,5
0,4
0,3
0,2
0,1
0,22
0,16
0
weiblich
männlich
Raucher
Nichtraucher
13
Darstellung
Geschlecht - Rauchverhalten
1
0,9
0,8
0,36
0,46
0,7
0,6
0,5
0,4
0,3
0,64
0,54
0,2
0,1
0
Raucher
Nichtraucher
weiblich
männlich
14
Darstellung
Geschlecht - Rauchverhalten
1
0,9
0,84
0,78
0,8
0,7
0,6
0,5
0,4
0,3
0,22
0,2
0,16
0,1
0
weiblich
männlich
Raucher
Nichtraucher
15
Darstellung
Geschlecht - Rauchverhalten
1
0,9
0,8
0,7
0,64
0,6
0,54
0,5
0,46
0,4
0,36
0,3
0,2
0,1
0
Raucher
Nichtraucher
weiblich
männlich
16
Darstellung
Geschlecht - Rauchverhalten
50
45
40
35
32
30
27
25
20
15
10
9
5
5
0
weiblich
männlich
Raucher
Nichtraucher
17
Darstellung
Geschlecht - Rauchverhalten
50
45
40
35
32
30
27
25
20
15
10
9
5
5
0
Raucher
Nichtraucher
weiblich
männlich
18
Korrelationskoeffizient
• Bravais-Pearson Korrelationskoeffizient rXY
• 2-dimensionales metrisch skaliertes
Merkmal (X,Y) mit Ausprägungen (aj,bk)
und Häufigkeiten hjk für j=1,…,l und
k=1,…,m.
• Maß für den Zusammenhang zw. X und Y:
l
rXY 
m
 (a
j1 k 1
j
n
 a)(b k  b)h jk
 l
 m

2
  (a j  a) h j   (b k  b) 2 h k 



 j1
 k 1

 (x
i 1
i
 x)(y i  y)
n
 n

2 
  (x i  x)   (y i  y) 2 
 i 1
 i 1

19
Korrelationskoeffizient
• rXY liegt immer im Intervall [-1,1]
• Extremfälle:
-1 negativer linearer Zusammenhang
rXY = 0 kein linearer Zusammenhang
1 positiver linearer Zusammenhang
• Interpretation:
– rXY < 0 d.h. große Werte von X treten mit kleinen
Werten von Y auf
– rXY > 0 d.h. große Werte von X treten mit großen
Werten von Y auf
20
Korrelationskoeffizient
• Probleme:
• Scheinkorrelation: X und Y hängen von einem
dritten Merkmal Z ab
– Bsp. Gefahr eines Waldbrandes (X) und schlechter
Kornertrag (Y) hängen von der Stärke der
Sonneneinstrahlung (Z) ab.
• Nonsenskorrelation: sachlogischer
Zusammenhang zw. X und Y
– Bsp. Korrelation zw. Anzahl der Störche und der
Anzahl der Geburten in einem Land
• Nichtlinearer Zusammenhang: rXY misst nur einen
linearer Zusammenhang
21
Korrelation
Korrelationskoeffizient = 0
Korrelationskoeffizient = 1
9
8
8
7
7
6
6
5
5
Y
Y
9
4
4
3
3
2
2
1
1
0
0
0
2
4
6
8
10
12
14
16
0
2
4
6
X
8
10
12
14
16
12
14
16
X
Korrelationskoeffizient = 0
Korrelationskoeffizient = - 1
18
8
16
7
14
6
12
5
10
Y
Y
9
4
8
3
6
2
4
1
2
0
0
0
2
4
6
8
X
10
12
14
16
0
2
4
6
8
10
X
22
Korrelation
Korrelationskoeffizient = - 0,58
Korrelationskoeffizient = 0,8
8
9
7
8
7
6
6
5
Y
Y
5
4
4
3
3
2
2
1
1
0
0
0
2
4
6
8
X
10
12
14
16
0
2
4
6
8
10
12
14
X
23
16
Korrelationskoeffizient
• Bsp. Körpergröße und Gewicht: r = 0,76
– Positiver linearer Zusammenhang zw.
Körpergröße und Gewicht.
120
100
Gewicht in kg
80
60
40
20
0
140
150
160
170
180
Größe in cm
190
200
210
24
Korrelation
• Fechnersche Korrelationskoeffizient (für 2
metrisch skalierte Merkmale X und Y): rF
• Basiert auf Vorzeichen der transformierten
Paare x* und y* (x i  x, yi  y)
1 x* und y* gleiches Vorzeichen od. beide 0
vi = ½ genau einer der Werte x* bzw. y* = 0
0 sonst
n
V  v i
i 1
25
Korrelation
• Fechnersche Korrelationskoeffizient:
2V  n
rF 
n
• Werte im Intervalle [-1,1]
• +1 nicht nur bei positivem linearen
Zusammenhang, sonder auch wenn gilt:
(x i  x und yi  y) oder (x i  x und yi  y)
26
Korrelation
• Bsp. Hennen, Körpergewicht, Legeleistung
Henne i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Gewicht xi
Leistung yi
xi*
yi*
vi
1763
1890
1872
1938
1791
1854
1960
1723
1898
1834
1946
1755
1846
1752
1884
1847
19
24
23
26
22
18
21
20
21
20
24
19
21
17
20
21
-84
43
25
91
-56
7
113
-124
51
-13
99
-92
-1
-95
37
-2
3
2
5
1
-3
0
-1
0
-1
3
-2
0
-4
-1
1
1
1
1
0
0
0,5
1
0,5
1
1
1
0,5
1
0
10,5
2  10,5  15 7
rF 

 0,4
15
15
27
Korrelation
• Rangkorrelationen für ordinal skalierte Merkmale:
• Verwendung von Rangzahlen: Merkmal Z,
Ausprägungen z1,…,zn, der Größe nach ordnen
(vom größten zum kleinsten Wert) z(1),…,z(n) und
nummerieren.
• Rangzahl: R(z(i)) = i für i=1,…,n
• Tritt ein Ausprägung mehrmals auf (Auftreten von
Bindungen), dann Rang = arithm. Mittel der
Ränge, die sie einnehmen.
– Bsp: z(1)=8, z(2)=5, z(3)=5, z(4)=2,
Ränge: R(z(1))=1, R(z(2))=2,5, R(z(3))=2,5, R(z(4))=4
28
Korrelation
• Spearmansche Rangkorrelationskoeffizient rS
• Entspricht dem Bravais-Pearson Koeffizienten der
Rangzahlen
n
rS 
 (R(x )  R(x))(R(y
i 1
i
i
)  R(y))
n
 n
2 
2
  (R(x i )  R(x))   (R(y i )  R(y)) 
 i 1
 i 1

• Wert +1 schon bei monoton wachsenden
Beobachtungen, d.h. es gilt für alle (xi,yi), (xj,yj):
mit xi < xj ist auch yi < yj
29
Korrelation
• Bsp. Klausur- und Übungspunkte
Student
Klausurpkt.
Rang K
UE-Pkt.
Rang UE
di
di²
1
76
1
122
1
0
2
44
6
67
8
-2
3
32
7
68
7
0
4
53
5
101
3
2
5
25
10
42
10
0
6
58
4
59
9
-5
7
26
9
118
2
7
8
59
3
79
6
-3
9
29
8
83
5
3
10
65
2
89
4
-2
0
4
0
4
0
25
49
9
9
4
• Einfachere Formel für den Spearman‘schen
Korrelationskoeffizienten (falls alle xi und yi
verschieden
sind (und di=R(xi)–R(yi)):
n
6 d i2
6  104
rS  1 
 1
 0,37
10(100  1)
n(n  1)
i 1
2
30
Korrelation
• Bsp. Maturanoten Mathe, Deutsch, Englisch
Mathe
Deutsch
Englisch
Mathe
1
0,23
0,382
Deutsch
0,23
1
0,576
Englisch
0,382
0,576
1
31
Korrelation
• Yulesche Assoziationskoeffizient für eine
Vierfeldertafel
• (X,Y) nominal skaliert
• Häufigkeitsverteilung von (X,Y)
A XY
h11h 22  h12h 21 f11f 22  f12f 21


h11h 22  h12h 21 f11f 22  f12f 21
• Es gilt:
-1 ≤ A ≤ +1; falls ein h =0, so gilt: |A |=1; Vorzeichen nur
in Verbindung Vierfeldertafel interpretierbar
XY
ij
XY
32
Korrelation
• Bsp. Geschlecht – Raucher/Nichtraucher
w
m

A XY
R
9
N-R
32

41
5
14
27
59
32
73
h11h 22  h12 h 21 9  27  32  5


 0, 21
h11h 22  h12 h 21 9  27  32  5
• Leicht positiver Zusammenhang zw.
Merkmalsausprägungen „w“ und „R“
33
Korrelation
• Bsp. Geschlecht – Raucher/Nichtraucher
m
w

A XY
R
5
N-R
27

32
9
14
32
59
41
73
h11h 22  h12 h 21 5  32  27  9


 0, 21
h11h 22  h12 h 21 5  32  27  9
• Leicht negativer Zusammenhang zw.
Merkmalsausprägungen „m“ und „R“
34
Theorie …
35
Wahrscheinlichkeitsrechung
• Betrachte Ereignisse die nicht
deterministisch (vorherbestimmbar) sind,
Ereignisse mit Zufallscharakter.
– Bsp. Werfen eines idealen Würfels, Werfen
einer fairen Münze, …
– Oder Ereignisse, die von so vielen
Einflussfaktoren abhängen, dass das Ergebnis
nicht sicher bestimmt werden kann.
36
Wahrscheinlichkeitsrechung
Grundbegriffe:
• Zufallsexperiment:
– Vorgang nach einer bestimmten Vorschrift
ausgeführt, beliebig oft wiederholbar, Ergebnis
hängt vom Zufall ab, bei mehrmaligen
Durchführung des Experiments beeinflussen
die Ergebnisse einander nicht – unabhängig
voneinander. (z.B. Münzwurf, Werfen eines
Würfels, …)
37
Wahrscheinlichkeitsrechung
• Elementarereignisse (Realisationen)
– Zufallsexperiment: Reihe aller möglichen
elementarer Ereignisse {e },…,{e }
1
n
• Ereignisraum S:
– Menge der Elementarereignisse S={e ,…,e }
1
n
• Ereignis:
– Jede beliebige Teilmenge des Ereignisraumes
(setzt sich aus einem od. mehreren
Elementarereignissen zusammen)
38
Wahrscheinlichkeitsrechung
• Vereinigung
– Vereinigung von 2 Ereignissen A und B: AUB Menge
aller Elementarereignisse, die zu A oder B gehören
• Durchschnitt
– Durchschnitt von 2 Ereignissen A und B: A∩B Menge
aller Elementarereignisse, die zu A und B gehören
• Disjunkte Ereignisse
– 2 Ereignisse A und B schließen einander aus, A∩B=Ø
(Ø unmögliches Ereignis)
• Komplementärereignis A
– Menge aller Elementarereignisse des Ereignisraumes S,
die nicht in Ereignis A enthalten sind
39
Wahrscheinlichkeitsrechung
• Wahrscheinlichkeit ist ein Maß zur
Quantifizierung der Sicherheit bzw.
Unsicherheit des Eintretens eines
bestimmten Ereignisses im Rahmen eines
Zufallsexperiments.
40
Wahrscheinlichkeitsrechung
• Klassischer Wahrscheinlichkeitsbegriff:
Zahl der günstigen Fälle
W(A) 
Zahl aller gleichmögl ichen Fälle
• Bsp. Urne mit 10 Kugeln (8 rot, 2 schwarz)
– Gesucht: Wahrscheinlichkeit, dass eine zufällig
gezogene Kugel rot ist (Ereignis A)
– Ereignisraum 10 mögl. Elementarereignisse, 8
günstige Fälle
– W(A) = 8 / 10 = 0,8
41
Wahrscheinlichkeitsrechung
• Statistischer Wahrscheinlichkeitsbegriff:
• Grenzwert der relativen Häufigkeiten des
Auftretens von A
h n (A)
W(A)  lim f n (A)  lim
n 
n 
n
42
Wahrscheinlichkeitsrechung
• Subjektiver Wahrscheinlichkeitsbegriff:
• Ereignissen werden „Wettchancen“
zugeordnet. Quote für A ist a:b, dann ergibt
sich die Wahrscheinlichkeiten
a
b
W(A) 
und W(A) 
ab
ab
43
Wahrscheinlichkeitsrechung
• Axiomatischer Wahrscheinlichkeitsbegriff:
• Definition von mathematischen
Eigenschaften
1. 0 ≤ W(A) ≤ 1
2. W(S) = 1
3. A und B disjunkt: W(A U B) = W(A) + W(B)
44
Zufallsvariable
• Zufallsvariable: Variable deren Wert vom
Zufall abhängt (z.B. X, Y, Z)
– Bsp. Zufallsexperiment: 2-maliges Werfen einer
Münze. Frage: Wie oft erscheint „Zahl“?
Mögliche Werte: 0, 1, 2. Variable „Anzahl
Zahl“ hängt vom Zufall ab – Zufallsvariable.
• Realisation (Ausprägung): Wert, den eine
Zufallsvariable X annimmt (z.B. x, y, z).
– Bsp. 2-maliges Werfen einer Münze, ZV X
„Anzahl Zahl“, Ausprägungen: x1=0, x2=1,
x3=2.
45
Zufallsvariable
• Zufallsvariable: Funktion, die jedem
Elementarereignis eine bestimmt reelle Zahl
zuordnet, z.B. X(ej)=xi
• Definitionsbereich einer ZV: Ereignisraum
S des zugrundeliegenden
Zufallsexperiments.
• Wertebereich einer ZV: Menge der reellen
Zahlen.
46
Zufallsvariable
• Diskrete Zufallsvariable: ZV mit endlich
vielen oder abzählbar unendlich vielen
Ausprägungen
• Stetige Zufallsvariable: können (zumindest
in einem bestimmten Bereich der reellen
Zahlen) jeden beliebigen Zahlenwert
annehmen.
47
Wahrscheinlichkeit
• Diskrete Zufallsvariable:
• Wahrscheinlichkeit, mit der eine diskrete
ZV X eine spezielle Ausprägung xi
annimmt, W(X=xi): Summe der
Wahrscheinlichkeiten derjenigen
Elementarereignisse ej, denen Ausprägung
xi zugeordnet ist:
W(X  x i ) 
 W(e )
X(e j )  x i
j
48
Wahrscheinlichkeitsfunktion
• Wahrscheinlichkeitsfunktion einer diskreten
ZV: Funktion f(xi), die für jede Ausprägung
der ZV (unterschiedliche Ausprägungen xi
einer ZV X) die Wahrscheinlichkeit ihres
Auftretens angibt: f(xi) = W(X=xi)
• Eigenschaften:
– f(xi) ≥ 0
– Σi f(xi) = 1
i=1,2,…
49
Verteilungsfunktion
• Verteilungsfunktion einer diskreten ZV:
Funktion F(x), die die Wahrscheinlichkeit
dafür angibt, dass die ZV X höchstens den
Wert x annimmt. F(x) = W(X ≤ x)
• Es gilt:
F(x)  W(X  x)   f(x i )
xi x
• Treppenfunktion
50
Verteilungsfunktion
• Verteilungsfunktion einer stetigen ZV (kann
in einem bestimmten Intervall jeden
beliebigen Wert annehmen): Funktion F(x),
die die Wahrscheinlichkeit dafür angibt,
dass die ZV X höchstens den Wert x
annimmt. F(x) = W(X ≤ x)
• Stetige Funktion
51
Verteilungsfunktion
• Eigenschaften einer stetigen Vt-Funktion:
1. 0 ≤ F(x) ≤ 1
2. F(x) ist monoton wachsend (d.h. für x1 < x2
gilt F(x1) ≤ F(x2)
3. lim x→-∞ F(x) = 0
4. lim x→∞ F(x) = 1
5. F(x) ist überall stetig
52
Wahrscheinlichkeitsdichte
• Wahrscheinlichkeitsdichte (Dichtefunktion)
f(x) einer stetigen ZV: Ableitung der
Verteilungsfunktion.
• Es gilt:
F´(x)  f(x)
x
F(x)   f(v)dv

53
Wahrscheinlichkeitsdichte
• Eigenschaften:
1. f(x) ≥ 0

2.  f(x)dx  1

b
3. W(a  X  b)   f(x)dx
a
4. W(X=x) = 0
5. W(a ≤ X ≤ b) = W(a < X < b)
6. W(X ≤ a) = F(a)
W(a ≤ X ≤ b) = F(b) – F(a)
W(X ≤ b) = F(b)
54
Parameter
• Charakterisierung der Wahrscheinlichkeitsverteilung von Zufallsvariablen durch
Parameter (Maßzahlen)
• Erwartungswert E(X) = Lageparameter
(Entspricht dem arithm. Mittel)
• Varianz Var(X) = Streuungsparameter
55
Erwartungswert
• Diskrete ZV:
E(X)   x i W(X  x i )  x i f(x i )
i
i
• Stetige ZV:

E(X) 
 x  f(x)dx

56
Varianz
• Diskrete ZV:
Var(X)   x i  E(X)  f(x i )
2
i
• Stetige ZV:

Var(X) 
 x  E(X)  f(x)dx
2

• Standardabweichung: σ X 
Var(X)
57
Standardisierung
• Lineare Transformation: Y = a + bX
• Spezialfall Standardisierung:
a = – E(X) / σX
b = 1 / σX
• Standardisierte Variable Z:
X  E(X)
Z
σX
• Es gilt: E(Z) = 0 und Var(Z) = 1
58
Theoretische Verteilungen
• Bedeutung von theoretische Verteilungen
• Deskriptive Statistik:
– Approximative funktionsmäßige Beschreibung
empirisch beobachteter Häufigkeitsverteilungen
• Mathematische Statistik:
– Wahrscheinlichkeiten für Ergebnisse
bestimmter Zufallsexperimente
59
Kombinatorik
• Wie kann eine gegebene Anzahl von
Elementen unterschiedlich angeordnet und
zu Gruppen zusammengefasst werden?
• Wie viele Möglichkeiten gibt es, n Elemente
anzuordnen? Anzahl der möglichen
Permutationen?
• Wie viele Möglichkeiten gibt es, von n
Elementen k auszuwählen? Anzahl der
möglichen Kombinationen?
60
Kombinatorik
• Permutationen:
• n voneinander verschiedene Elemente:
n! = n·(n-1)·(n-2)·…·1 Permutationen
• Bsp.1: n=3, Elemente e1, e2, e3. Anzahl der
möglichen Permutationen: 3! = 3·2·1 = 6
(e1, e2, e3) (e1, e3, e2) (e2, e1, e3) (e2, e3, e1)
(e3, e1, e2) (e3, e2, e1)
• Bsp.2: n=10, Anzahl der möglichen
Permutationen: 10! = 3 628 800
61
Kombinatorik
• n Elemente, wobei ni Elemente vom Typ i
sind (r unterschiedliche Typen):
n!
n1!...  n r !
• Bsp.1: n=10, r=3 und n1=3, n2=5, n3=2,
Anzahl der möglichen Permutationen:
10!
3628800

 2520
3!5!2! 6 120  2
62
Kombinatorik
• Kombinationen:
• Aus n verschiedene Elemente sollen k Stück
gewählt werden
– Kombination ohne Wiederholung: jedes
Element kann nur einmal gewählt werden
• Berücksichtigung der Reihenfolge:
n!
Anzahl der Möglichkeiten:
(n  k)!
• Keine Berücksichtigung der Reihenfolge:
Anzahl der Möglichkeiten:  n 
n!
  
 k  k!(n  k)!
63
Kombinatorik
• Kombinationen ohne Wiederholung:
• n=3, k=2, Elemente e1, e2, e3.
– Berücksichtigung der Reihenfolge:
Möglichkeiten: (e1, e2) (e2, e1) (e1, e3) (e3, e1)
(e2, e3) (e3, e2), also 3!/(3-2)! = 6 Möglichkeiten
– Keine Berücksichtigung der Reihenfolge:
Möglichkeiten: (e1, e2), (e1, e3) (e2, e3), also
3!/(2!(3-2)!) = 3 Möglichkeiten
64
Kombinatorik
• Kombinationen ohne Wiederholung:
• Bsp.1: Lotto, Möglichkeiten aus 49 Zahlen
6 zu wählen (Reihenfolge unberücksichtigt)
 49 
   13 983 816
6
• Bsp.2: Pferderennen, sind 8 Pferde am Start,
gibt es für die Belegung der ersten 3 Plätze
8!/(8-3)! = 336 Möglichkeiten
65
Kombinatorik
• Aus n verschiedene Elemente sollen k Stück
gewählt werden
– Kombination mit Wiederholung: ein Element
kann auch mehrfach ausgewählt werden.
• Berücksichtigung der Reihenfolge
Anzahl der Möglichkeiten: nk
• Keine Berücksichtigung der Reihenfolge
Anzahl der Möglichkeiten:
 n  k  1 (n  k  1)!

 
 k  k!(n  1)!
66
Kombinatorik
• Kombination mit Wiederholung:
• n=3, k=2, Elemente e1, e2, e3.
– Berücksichtigung der Reihenfolge,
Möglichkeiten: (e1, e1), (e1, e2), (e1, e3), (e2, e2),
(e2, e1), (e2, e3), (e3, e3), (e3, e1), (e3, e2), Anzahl
der Möglichkeiten: nk = 3² = 9
– Keine Berücksichtigung der Reihenfolge,
Möglichkeiten: (e1, e1), (e1, e2), (e1, e3), (e2, e2),
(e2, e3), (e3, e3), Anzahl der Möglichkeiten:
(3+2-1)! / (2!·(3-1)!) = 4! / (2!·2!) = 6
67
Kombinatorik
• Kombinationen mit Wiederholung:
• Bsp.1: Würfelt man viermal hintereinander,
sind 64 = Abläufe möglich
• Bsp.2: Hat man vier verschiedene Sorten
Süßigkeiten, gibt es 286 Möglichkeiten eine
Tüte mit 10 Süßigkeiten zu füllen.
 4  10  1

  286
 10 
68
Theoretische Verteilungen
• Diskrete Verteilungen
–
–
–
–
Binomialverteilung
Hypergeometrische Verteilung
Poissonverteilung
...
• Stetige Verteilungen
–
–
–
–
–
–
–
Gleichverteilung
Exponentialverteilung
Normalverteilung
Chi-Quadrat Verteilung
t-Verteilung (Studentverteilung)
F-Verteilung
...
69
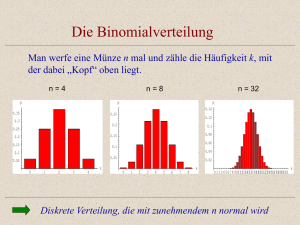
Binomialverteilung
• Wahrscheinlichkeiten für die Häufigkeit des
Eintreffens bestimmter Ereignisse bei
Bernoulli-Experimenten berechnen.
• Bernoulli-Experiment: Folge von BernoulliVersuchen. Urnenmodell mit Zurücklegen
– Es gibt nur 2 mögliche Ausgänge: A und Ā
– Wahrscheinlichkeiten für Eintreten von A (θ)
und Ā (1- θ) sind konstant
– Versuche sind voneinander unabhängig.
70
Binomialverteilung
• Bsp. Bernoulli-Experiment:
– fünfmaliges Werfen einer Münze,
Zufallsvariable X „Anzahl der Zahlen“,
Realisation x = 0, 1, 2, 3, 4, 5
– Wahrscheinlichkeiten für Eintreten von A:
W(X=x) = f(x) = ?
71
Binomialverteilung
• Wahrscheinlichkeit des Auftretens einer
bestimmten Realisation x: W(X=x) = f(x)
• Wahrscheinlichkeitsfunktion der
Binomialverteilung:
 n  x
 θ (1  θ) n  x
f B (x; n, θ)   x 
für x  0,1,..., n
 0
sonst

72
Binomialverteilung
• Bsp. Münzwurf (n=5), Wahrscheinlichkeit
dass genau 2-mal Zahl geworfen wird:
W(X=2)
 5 2
f B (2;5,0.5)   0,5 (1  0,5)52  0,3125
 2
73
Binomialverteilung
• Wahrscheinlichkeit, dass die Zufallsvariable
X höchstens den Wert x annimmt:
Verteilungsfunktion FB(x;n,θ)
n x
n -x
FB (x; n, θ)    θ (1  θ)
i 0  x 
x
74
Binomialverteilung
• Bsp. Münzwurf (n=5), Wahrscheinlichkeit
dass höchstens 2-mal Zahl geworfen wird:
W(X  2)
 5 2
FB (2;5,0.5)    0,5 (1  0,5)5-2  0,5
i 0  2 
2
75
Binomialverteilung
• Erwartungswert der Binomialverteilung:
E(X) = n·θ
• Varianz der Binomialverteilung:
Var(X) = n·θ·(1-θ)
• Bsp. Münzwurf:
– E(X) = 5·0,5 = 2,5
– Var(X) = 5·0,5·(1-0,5) = 1,25
76
Hypergeometrische Verteilung
• Urnenmodell Ziehen ohne Zurücklegen:
– Urne mit N Kugeln (M schwarze, N-M weißen)
– Zufallsstichprobe: ziehe n Kugeln ohne
Zurücklegen
– Wahrscheinlichkeit, dass unter den n gezogenen
Kugeln genau x schwarze zu finden sind?
• Ziehen ohne Zurücklegen, keine
Berücksichtigung der Reihenfolge.
77
Hypergeometrische Verteilung
• Urnenmodell:
– Aus M schwarzen Kugeln genau x auswählen: Anzahl
der Kombinationen  Mx 
 
– Aus N-M weißen Kugeln genau n-x auswählen: Anzahl
 N-M 
der Kombinationen  n-x 
– Jede mögl. Stpr. „x schwarze aus M“ kann mit jeder
mögl. Stpr. „n-x weiße aus N-M“ kombiniert werden.
– Daher: Gesamtzahl der Möglichkeiten genau x
N-M 
schwarze zu ziehen:  Mx 


  n-x 
– Gesamtzahl der Möglichkeiten aus N Kugeln n zu
ziehen:  Nn 
 
78
Hypergeometrische Verteilung
• Wahrscheinlichkeit genau n schwarz Kugeln
 M   N-M 
 

zu ziehen:
 x   n-x 
 N
 
n
• Wahrscheinlichkeitsfunktion der
Hypergeometrischen Verteilung:
  M  N-M 
  

x
n-x

  
f H (x;N,n,M)= 
für x=0,1,...,n
 N
 

n

 0
sonst
79
Hypergeometrische Verteilung
• Verteilungsfunktion: Summation der
Einzelwahrscheinlichkeiten
• Liefert Wahrscheinlichkeit für „höchstens x
schwarze Kugeln“
80
Hypergeometrische Verteilung
• Bsp. Sortiment von N=8 Dioden, es werden
n=3 zufällig gezogen (ohne Zurücklegen),
M=5 der Dioden sind defekt.
• Ges: Wahrscheinlichkeit, dass genau 2 (=x)
der 3 gezogenen Dioden defekt sind.
 M  N-M   5  8-5 
 
   
x
n-x
2  3-2  10  3




P(X=x)=
=
=
=0,5357
56
 N
 8
 
 
n
 
 3
81
Hypergeometrische Verteilung
• Erwartungswert:
E(X) = n · M/N
• Varianz
Var(X) = n · M/N · (N-M)/N · (N-n)/(n-1)
• Approximation durch Binomialverteilung:
– Wenn N, M, N-M groß und n klein, Parameter
der Binomialverteilung: θ = M/N
– Faustregel: Approximation, wenn n/N < 0,05
82
Poissonverteilung
• Verteilung seltener Ereignisse
• Große Zahl von Versuchen n,
Wahrscheinlichkeit θ für Auftreten eines
Ereignisses sehr klein
• Wahrscheinlichkeitsfunktion:
 μ x e-μ

f P (x;μ)=  x! für x=0,1,...
0sonst

83
Poissonverteilung
• Erwartungswert: E(X) = μ
• Varianz: Var(X) = μ
• Approximation der Binomialverteilung
durch die Poissonverteilung:
– n groß und θ klein, Parameter μ = n·θ
– Faustregel: n > 10 und θ < 0,05.
• Approximation der Hypergeometrischen Vt.
– M/N = θ klein, N im Vergleich zu n groß,
Parameter μ = n · M/N
– Faustregel: M/N < 0,05 und n/N < 0,05
84
Poissonverteilung
• Bsp. Wahrscheinlichkeit bei einer Prüfung
von n=2000 Buchungen genau 3 (=x)
Fehlbuchungen zu finden, Anteil der
Fehlbuchungen: θ=0,001.
• Poissonverteilung: μ = n·θ = 2
μ x e-μ 23e-2
W(X=x)=
=
=0,1804
x!
3!
85
Gleichverteilung
• Diskrete Zufallsvariable:
• Jede der k möglichen Ausprägungen hat
gleiche Wahrscheinlichkeit
P(X=xi) = 1/k
(i=1,…,k)
• Bsp. Wahrscheinlichkeitsverteilung der
Augenzahl eines idealen Würfels:
P(X=xi) = 1/6
(i=1,…,6)
86
Gleichverteilung
• Stetige Zufallsvariable:
• Realisationen der stetigen Zufallsvariablen
X liegen im Intervall [a;b]
• Dichtefunktion:
 1
für a  x  b

f G (x;a,b)=  b-a
 0
sonst
• P(x  X  x+Δx) = 1/(b-a) · Δx
87
Gleichverteilung
Stetige Gleichverteilung
0,2
P(xXx+Δx) =
1 /(b -a ) · Δ x
f(x;a,b)
1/(b-a)
0
0
a
x
x+Δx
14
b
x
88
Gleichverteilung
• Verteilungsfunktion (Integration der Dichte)
für x<a
 0
 x-a

FG (x;a,b)= 
für a  x  b
 b-a
für x>b
 1
89
Gleichverteilung
Stetige Gleichverteilung
1,2
1
F(x;a,b)
0,8
0,6
0,4
0,2
0
0
a
14
b
x
90
Gleichverteilung
• Erwartungswert: E(X) = (a+b)/2
• Varianz: Var(X) = (b-a)² / 12
• Bsp. Wegzeit ist gleichverteilt im Intervall
[30;40]. Ges. Wahrscheinlichkeit zw. 32 und
35 Min. zu benötigen.
P(32  X  35) = 1/(b-a) · Δx
= 1/(40-30) · (35-32) = 0,3
Durchschnittlich benötigte Zeit: E(X) = 35
91
Normalverteilung
• Wichtigste theoretische Verteilung:
• Normalverteilung:
–
–
–
–
–
–
–
stetige Verteilung
symmetrische Dichtefunktion
S-förmige Verteilungsfunktion
Erwartungswert: E(X) = µ
Varianz: Var(X) = σ²
Maximum der Dichte bei x=µ
Wendepunkte bei x=µσ
92
Normalverteilungen
• Normalverteilung:
• Dichtefunktion (für -∞<x<+∞ und σ>0) :
1
f n (x; μ, σ ) 
2
2π 2
e
1  x μ 
 

2 σ 
2
• Verteilungsfunktion:
x
Fn (x; μ, σ ) 
2


1
2 2
e
1  v μ 
 

2 σ 
2
dv
93
Normalverteilung
• Normalverteilungen mit unterschiedlichen
Parametern
Normalverteilung
0,45
0,4
0,35
0,3
f(x)
0,25
0,2
0,15
0,1
0,05
0
-6
-4
-2
0
2
4
6
x
N(4,3)
N(0,1)
8
10
12
94
N(2,2)
Normalverteilung
• Verteilungsfunktion
Verteilungsfunktion Normalverteilung
1
0,9
0,8
0,7
F(x)
0,6
0,5
0,4
0,3
0,2
0,1
0
-4
-3
µ-3σ
-2
µ-2σ
-1
0
1
µ-σ
µ
x
µ+σ
2
µ+2σ
3
µ+3σ
4
95
Normalverteilung
• Standardnormalverteilung:
– Erwartungswert µ = 0
– Varianz σ² = 1
• Dichtefunktion:
f n (z;0,1) 
1
2π
e
1
 z2
2
96
Normalverteilung
• Standardnormalverteilung
Standardnormalverteilung
0,5
99,73%
0,45
95,45%
68,27%
0,4
0,35
f(z)
0,3
WP
0,25
WP
0,2
0,15
0,1
0,05
0
-4
-3
-2
-1
0
z
1
2
3
97
4
Normalverteilung
• Approximation durch Normalverteilung:
Mit wachsendem n nähern sich viele
theoretische Vt. der Normalverteilung
• Empirische Verteilungen lassen sich
ebenfalls oft durch die N-Vt. annähern.
98
Normalverteilung
• Reproduktionseigenschaft (od. Additivitätseigenschaft) der Normal-Vt.
• Additionstheorem der Normalverteilung:
– Die Summe (X) von n unabhängig normalverteilten
Zufallvariablen X1,…,Xn ist ebenfalls normalverteilt.
X = X1 + … + Xn
– Der Erwartungswert von X ist die Summe der einzelnen
Erwartungswerte μ1,…,μn
E(X) = μ = μ1 + … + μn
– Die Varianz von X ist die Summe der einzelnen
Varianzen σ1²,…σn²
Var(X) = σ² = σ1² + … + σn²
99