Weizen (t)

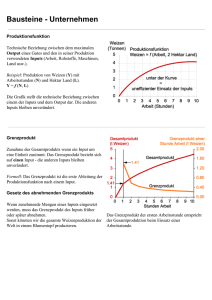
Mikroökonomie 1
Angebot des Unternehmen
4.1.07
1
Marktform der vollständigen Konkurrenz

Für das einzelne Unternehmen ist der Preis vom Markt
gegeben.

Mögliche Ursachen:
 Vielzahl von Nachfragern und Anbietern (keine
Preisabsprachen möglich)
 Homogenes Gut (Produkt eines Anbieters unterscheidet
sich nicht von dem seiner Konkurrenten)
 Neue Unternehmen können jederzeit in den Markt
einsteigen (Extra-Gewinne verschwinden)
2
Wie viel produzieren?
Mehr produzieren, wenn die Produktionskosten der
letzten Einheit kleiner als ihr Verkaufsertrag sind.
Preis
Kosten
Grenzkosten
800
600
500
Marktpreis = 500
400
Grenzkosten = 340
200
0
0
5
9 10
15
20
Weizen (t)
3
Wie viel produzieren?
Weniger produzieren, wenn die Produktionskosten der
letzten Einheit grösser als ihr Verkaufsertrag sind.
Preis
Kosten
Grenzkosten
800
Grenzkosten = 580
600
500
Grenzkosten = 500
400
200
gewinnmaximierende
Menge = 13 t Weizen
0
0
5
10
13 15
20
Weizen (t)
4
Wie gross ist der Gewinn?
Gewinn = Gesamtertrag - Gesamtkosten
Durchschnittskosten
Preis
Kosten
Grenzkosten
800
600
500
Marktpreis = 500
400
Gewinn
200
Ertrag
Kosten
= Preis mal Menge
= Durchschnittskosten mal Menge
0
0
5
10
13 15
20
Weizen (t)
5
Gesamtertrag
Gesamtkosten
6500
Gesamtkosten
6000
Gewinn = 2120 Fr.
4380
4000
2000
0
0
5
10
15
20
Preis
Kosten
Weizen (t)
Grenzkosten
800
möglicher Gewinn
weniger Gewinn
600
500
Durchschnittskosten
400
200
0
0
5
8
10
13
15
20
Weizen (t)
6
Was geschieht,
wenn der Preis steigt?
Durchschnittskosten
Preis
Kosten
Grenzkosten
das Angebot
steigt
800
700
600
600
500
400
200
0
0
5
10
15
20
Weizen (t)
7
Was geschieht,
wenn der Preis sinkt?
Durchschnittskosten
Preis
Kosten
Grenzkosten
das Angebot
sinkt
800
600
500
400
400
300
200
0
0
5
10
15
20
Weizen (t)
8
Was geschieht, wenn der Preis unter
die Durchschnittskosten sinkt?
Durchschnittskosten
Preis
Kosten
Grenzkosten
Das Unternehmen
macht einen
Verlust.
800
Was passiert mit
dem Angebot ?
600
400
300
200
200
Verlust
0
0
5
10
15
20
Weizen (t)
9
Angebot bei Verlust
Kosten pro
t Weizen
Grenzkosten
800
Verlust bei Produktion
600
Durchschnittskosten
400
300
200
200
variable Durchschnittskosten
Verlust
Fixkosten
fixe Durchschnittskosten
0
0
5
10
15
Verlust ohne Produktion
20
Weizen (t)
10
Der Ertrag deckt die variablen Kosten
und einen Teil der Fixkosten.
Angebot bei Verlust
Angebot
5
0
(Produktion
eingestellt)



Ertrag
Kosten
5 x 200 = 1000
Total = 1500
Fix = 1000
Variabel = 500
Total = 1000
Fix = 1000
Variabel = 0
0
Verlust
1000 – 1500 = -500
0 - 1000 = -1000
Kurzfristig geht es darum, den Verlust zu minimieren.
Kurzfristig wird angeboten, wenn wenigstens die variablen
Kosten und ein Teil der Fixkosten gedeckt werden.
Langfristig wird nur angeboten, wenn alle Kosten gedeckt
werden.
11
Flash-Simulation Unternehmen
12
Wenn es zwei Mengen gibt bei denen MC = p
MC
100
80
AC
p60
AVC
40
20
AFC
0
0
1
2
3
4
200
5
6
7
8
9
10
7
8
9
10
Gewinn
100
0
-100
-200
0
1
2
3
4
5
6
13
Inverse Angebotskurve
Welchen Preis verlangt das Unternehmen für eine bestimmte Menge
Output.
Unternehmen A
Unternehmen B
p
p
p=MCA(y)
y
p=MCB(y)
y
14
Produzentenrente 1
Gewinn:
py  cv  y   F
Produzentenrente:
py  cv  y 
MC
p
AC
p*
AVC
AFC
y*
y
15
Produzentenrente 2
Produzentenrente:
py  cv  y 
MC
p
?
AC
p*
AVC
Fläche unter Grenkostenkurve
= variable Kosten
AFC
y*
y
16
Produzentenrente 3
Produzentenrente:
py  cv  y 
MC
p
AC
p*
AVC
AFC
y*
y
17
Beispiel Produzentenrente


Wichtiges Instrument bei der Wohlfahrtsanalyse von
Marktereignissen und –eingriffen.
Veränderung entspricht einer Gewinnveränderung
(kurzfristig).
Beispiel:
höherer staatlicher
Preis für Milch
p
Angebot
Nachfrage
y
18
Beispiel zu Angebotskurve
2
Kostenfunktion: c  y   y  1
p  2y
p
Angebotsfunktion: S  p   y 
p  AVC ?
Gewinnfunktion:
S  p  y 
p
2
  p   py  c  y 
p
2
AC
AVC
2
2
p  p
 p    1
2 2
p2 p2
p2


1 
1
2
4
4
1
y
p2
 1  p 
Produzentenrente: A     p 
4
 2  2 
19
langfristige Angebotskurve

Menge die bei der optimalen Grösse der fixen Inputs
produziert wird.
kurzfristig:
langfristig:
p  MC  y, k 
p  MCl  y   MC  y, k  y  
mit
mit
py  cv  y   0
py  c  y   0
cv  y 
p
y
c y
p
y
20
langfristige Angebotskurve

Die langfristige Angebotskurve ist preiselasticher.
p
kurfristig
langfristig
y*
y
21
langfristige Angebotskurve

Bei langfristig konstanten Durchschnittskosten
 langfristige Grenzkostenkurve = langfristige
Durchschnittskostenkurve
 jede beliebige Menge wird zum Preis
p  cmin
angeboten
p
p  cmin
langfristig
y
22
langfristige Durchschnittskosten
kleiner Bauer hat 10 ha Land
grosser Bauer hat 30 ha Land
Grenzkosten
kleiner Bauer
Durchschnittskosten
kleiner Bauer
1000
Kosten pro Eiheit
Grenzkosten
grosser Bauer
800
600
Durchschnittskosten
grosser Bauer
400
konstante langfristige DK
200
0
0
5
10
Weizen (t)
15
20
25
23