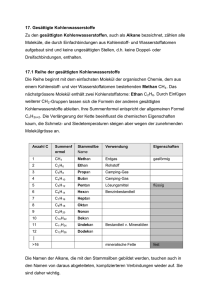
Kapitel 2: Quantenstruktur von Molekülen

Kapitel 2:
Quantenstruktur von Molekülen
Übersicht:
2.1 Der molekulare Hamiltonoperator
2.2 Die Born-Oppenheimer-Näherung
2.3 Die Schrödingergleichung für die Kernbewegung
2.4 Die Born-Oppenheimer-Potentialfläche
2.5 Modellpotentiale
2.6 Separation der Wellenfunktion
für die Kernbewegung
2.7 Schwingungsbewegung von Molekülen:
Normalkoordinatenanalyse
2.8 Drehimpuls in der Quantenmechanik
2.9 Drehbewegung von Molekülen
2.10 Drehimpuls-Kopplungshierarchien
in Molekülen
Literatur:
Atkins, Molecular Quantum Mechanics, 4. ed.: Kapitel 4,8,10, 11
Primas, Müller-Herold, Elementare Quantenchemie: Kapitel 4
Kapitel
2.1 Der Molekulare Hamiltonoperator
2.2 Die Born-Oppenheimer-Näherung
2.3 Die Schrödingergleichung für die Kernbewegung
→ Tafel
2.4 Die Born-Oppenheimer-Potentialfläche
2.4.1 Eigenschaften
Die Bewegungen der Elektronen und der Kerne können daher in sehr guter
Näherung voneinander getrennt werden (Born-Oppenheimer-Näherung). Die
schnellen Elektronen “sehen” daher immer ein starres Kerngerüst und ihre
Wellenfunktionen passen sich instantan an, wenn sich die Geometrie der Kerne
ändert, um die Energie zu minimisieren.
Da Kerne erfahren bei ihrer Bewegung die sich verändernde elektronische
Energie als eine effektive potentielle Energie*. Diese wird als Born-Oppenheimer
(BO)-Potential bezeichnet und stellt das intramolekulare Potential für die
Bewegung der Kerne dar.
* Eine Potential ist definiert als eine Energie, die nur von der Lage (d.h. den Ortskoordinaten) abhängt.
Für mehratomige Moleküle ist das Born-Oppenheimer-Potential eine
mehrdimensional Funktion der Koordinaten aller Kerne im Molekül. Man spricht
daher von einer mehrdimensionalen Born-Oppenheimer-Potentialhyperfläche.
Ein stabiles Molekül entspricht einem Minimum der BO-Hyperfläche. Die
entsprechende Kernkonfiguration wird als Gleichgewichtsgeometrie des
Moleküls bezeichnet.
Die BO-PF hängt nicht von den Kernmassen ab und ist insbesondere identisch
für alle Isotopomere eines Moleküls (z.B. H2, HD und D2)
2.4.2 Interne und externe Bewegungsfreiheitsgrade eines Moleküls
Für die weitere Diskussion des BO-Potentials müssen wir zwischen internen und
externen Bewegungsfreiheitsgraden (FG) eines Moleküls unterscheiden. Jedem
FG entspricht eine Koordinate der Bewegung.
Analyse der möglichen Bewegungen:
1. Ein Atom kann sich in alle drei räumlichen Dimensionen (x,y,z) bewegen
→ 3 FG für die Bewegung in x,y,z
2. Ein Molekül bestehend aus K Atomen kann als Ansammlung seiner Atome
betrachtet werden → 3K FG für die Bewegung jedes Atoms in x,y,z
Die Bewegungen der Atome im Molekül sind jedoch nicht unabhängig voneinander:
•
Das Molekül kann sich als ganzes bewegen: Translation
→ 3 FG
•
Das Molekül kann als ganzes rotieren: Rotation: lineare Moleküle
nicht-lineare Mol.
→ 2 FG
→ 3 FG
•
Die restlichen 3K-3-2=3K-5 (lineare Mol.) bzw. 3K-6 (nicht-lineare Mol.) FG
entsprechen den Schwingungen (Vibrationen) des Moleküls
Translation und Rotation werden als externe Bewegungsfreiheitsgrade bezeichnet,
da sie die Bewegung des Moleküls als ganzes betreffen.
Die Molekülschwingungen entsprechen den internen Bewegungsfreiheitsgraden,
da sich dabei die relative Lage der Kerne zueinander ändert:
Lineare Moleküle:
Nicht-lineare Moleküle:
3K-5 interne FG = interne Koordinaten
3K-6 interne FG = interne Koordinaten
Die elektronische Energie hängt offensichtlich nur von der Lage der Kerne relativ
zueinander ab. Die BO-Hyperfläche ist somit nur eine Funktion der 3K-5 (3K-6)
internen Koordinaten.
rij
Welche internen Koordinaten wählt man nun zur
Darstellung der BO-Hyperfläche ?
Zweckmässig sind (a) Bindungslängen rij, (b)
Bindungswinkel θijk und (c) Dihedralwinkel Φijkl
oder allgemeine Schwingungskoordinaten
(Normalkoordinaten, s. Abschn. 2.7).
2.4.3 Beispiele
Energie
BO-Energie U(r)≣V(r)
Zweiatomige Moleküle: das Wasserstoff-Molekül H2
Gleichgewichtsabstand
(=Bindungslänge)
req
Kernabstand r
H
H
Getrennte Atome bei R=∞
Totale Energie Eel=2 x E1s
Dissoziationsenergie
= benötigte Energie zur
Trennung der Bindung
HH
Optimaler Überlapp der 1s AOs
beim Gleichgewichtsabstand = minimale Energie
Bem.: Für das BO-Potential wird in der Literatur oft das Symbol V statt U
verwendet, um zu unterstreichen, dass es sich um ein Potential handelt.
Dreiatomige Moleküle: das Ozon-Kation O3+
•
3K-6=3 interne Koordinaten: BO-Potential=3-dim. Funktion →
nur Schnitte durch die Potentialfunktion darstellbar
•
BO-Potential entlang der
Bindungswinkel-Koordinate
Θ213
2D-Kontourplot des BOPotentials entlang den
Bindungslängen r12 and r13.
Minimum =
Gleichgewichtsgeometrie
r12 / Å
•
r12 1 r13
2 Θ213 3
r12,eq
GleichgewichtsBindungswinkel
Θeq
r13,eq
r13 / Å
Mehratomige Moleküle: grosse Anzahl interner Freiheitsgrade, man stellt wiederum
nur Schnitte oder vielfach auch nur die relativen Energien von stationären Punkten
(=Minima entsprechend stabilen Konfigurationen des Moleküls und Sattelpunkte
entsprechend Übergangszuständen (=Barrieren, Sattelpunkten)) auf der BOPotential-Hyperfläche dar
Bsp.: Cyclopentadien C5H6:
potentielle Energie V
Übergangszustände
(Sattelpunkte, Barrieren)
Illustration von
Minima und Übergangszuständen
Cyclopentadien
Übergangszustand
(Barriere, Sattelpunkt)
Minimum
(stabiles
Molekül)
Allen und Ethin
stabile Isomere
(Minima auf der selben
(Minima auf der
Potential-Hyperfläche) Potential-Hyperfläche)
Minimum
(stabiles Molekül)
Chemische Reaktionen verfolgen einen Pfad minimaler Energie auf der
Potentialhyperfläche (s. Kapitel 4)
Bsp.: F + HCl → HF + Cl
Reaktanden
F + HCl
Übergangszustand
(Sattelpunkt, Barriere)
Eine chemische Reaktion ist
vollständig durch die
zugrundeliegende BOPotentialfläche bestimmt !
Produkte
Cl + HF
M.P. Deskevich et al., J. Chem. Phys 124 (2006), Art. No. 224303
Ein Molekül ohne Struktur: CH5+
•
CH5+ ist ein wichtiges Molekül in Chemischer-IonisationsMassenspektrometrie (Protonendonor !) und der Chemie des
interstellaren Raumes
•
Das globale Minimum der BO-PF wurde als eine
Struktur mit C2v-Symmetrie bestimmt, die als ein CH3+
aufgefasst werden kann, das an ein H2 gebunden ist
•
CH3
+
Die Potentialbarrieren entlang internen
Koordinaten, die zu einem Austausch aller 5
H-Atome im Molekül führen, sind jedoch sehr
klein (kleiner als die Nullpunktsenergie des
Moleküls !)
E.T. White et al., Science 284 (1999), 135
X. Huang et al., Science 311 (2006), 60
H2
•
CH5+ ist daher ein extrem fluxionales,
strukturloses Molekül, das am besten als
ein Kohlenstoff-Kation aufgefasst werden
kann, um das 5 H-Atome kreisen.
•
Eine befriedigende theoretische
Beschreibung für CH5+ existiert bisher noch
nicht ...
Moleküldynamik-Simulationen
von CH5+
CH4
CH5+
© Gruppe Marx, Ruhr-Uni Bochum
2.5 Modellpotentiale
Die Berechnung einer vollständigen BO-Hyperfläche mit quantenchemischen
Methoden ist extrem (!) aufwändig und derzeit (2013) nur für maximal
sechsatomige Moleküle machbar. Man verwendet daher häufig analytische
Modellpotentiale um Bereiche der BO-Hyperfläche - in der Regel eindimensionale
Schnitte entlang bestimmter internen Koordinaten - zu approximieren.
harmonisch
2.5.1 Harmonische Potentialfunktion
•
einfachste mögliche Potentialfunktion:
(2.5.1)
k ... Kraftkonstante
r ... irgendeine interne Koordinate
•
gute Näherung an das tatsächliche BO-Potential
nahe an der Gleichgewichtsgeometrie req
•
wird bei grossen Auslenkungen aus der
Gleichgewichtslage (r-req) unphysikalisch, da es
keine Dissoziation des Moleküls erlaubt
BO
Harmonische Näherung des BO-Potentials
für ein zweiatomiges Molekül
•
Die Kraftkonstante k kann aus der zweiten Ableitung des BO-Potentials V(r)
bei der Gleichgewichtsgeometrie req berechnet werden
2
k=
V (r )
r2
(2.5.2)
r =req
2.5.2 Anharmonische Potentialfunktion
•
Die harmonische Näherung kann als erstes Glied einer TaylorreihenApproximation des BO-Potentials um die Gleichgewichtsgeometrie
aufgefasst werden, die durch die Berücksichtigung von Termen höherer
Ordnung (=Anharmonizitäten) systematisch verbessert werden kann:
(2.5.3)
kubische
quartische
Anharmonizität Anharmonizität
•
Diese Form von Reihenentwicklung ist der in der Praxis am häufigsten
gebrauchte Ansatz, da sie eine beliebig genaue Approximation des BOPotentials erlaubt.
•
Siehe hierzu auch Übung 2.
2.5.3 Morse-Potentialfunktion
•
einfaches Modellpotential, das Anharmonizitäten und Dissoziationsverhalten
berücksichtigt:
(2.5.4)
De ... Dissoziationsenergie
k ... harmonische Kraftkonstante
•
gute Nährung an das BO-Potential für
Streckbewegungen (Verlängerung von
Bindungsabständen rij)
•
nicht geeignet für Knickbewegungen
θijk oder Torsionen Φijkl
_______________________________________________________________________________
•
Parameter für die Morse-Potentialfunktion (Beispiele)
Morse-Potentialparameter von ausgewählten zweitomigen Molekülen:
Gleichgewichtsabstände Re, Dissoziationsenergien De, Kraftkonstanten k zweiatomiger Moleküle.
rReqe /pm
De / eV
k /N m- 1
rReqe /pm
De / eV
k /N m- 1
H2
74.1
4.748
576
H2+
105.2
2.793
160
CH
112.0
3.642
448
H Cl
127.5
4.618
517
OH
097.0
4.624
782
N a2
307.9
0.730
17
CO
112.8
11.226
1905
S2
188.9
4.414
497
N2
109.8
9.905
2299
C l2
198.8
2.514
324
NO
115.1
6.615
1597
N a Cl
236.1
4.23
110
O2
120.8
5.214
1178
A g Cl
228.1
3.24
183
Ne 2
310.
0.0035
0.41
(N.B. 1eV = 96.4846 kJ/mol)
(Daten aus K.P. Huber, G. Herzberg, Constants of Diatomic Molecules, Van Nostrand 1979)
2.5.4 Potentiale für interne Drehbewegungen (Torsionen)
•
Interne Rotationen = Drehung bestimmter Teile eines Moleküls (z.B.
Methylgruppen)
•
Die Potentialfunktion für interne Rotationsbewegungen ist periodisch:
Ethan C2H6
Butan C4H10
ϕ ... Dihedral-(Torsions-) Winkel
ϕ
ϕ
Ethan C2H6
Butan C4H10
ϕ ... Dihedral-(Torsions-) Winkel
ϕ
Konformere
•
•
•
Torsionspotentiale werden üblicherweise durch Summen von trigonometrischen Funktionen ausgedrückt (Fourier-Reihenentwicklung):
⇥ V2
⇥ V3
⇥
V1
V( )=
1 + cos +
1 cos 2 +
1 + cos 3
(2.5.5)
2
2
2
Interne Rotationen sind in Biomolekülen (Peptide, Proteine, RNA, DNA) von
herausragender Bedeutung.
Die verschiedenen Rotationsisomere werden als Konformere bezeichnet.
Definition: eine Konformation ist eine spezifische räumliche Anordnung eines
Makromoleküls entsprechend einem Minimum auf der BO-Potentialfläche.
Konformere sind Stereoisomere, die durch interne Rotationen ineinander
überführt werden können.
2.6 Separation der Wellenfunktion für die Kernbewegung
Die verschiedenen Formen der Bewegung eines Moleküls passieren auf
verschiedenen Zeitskalen:
•
•
•
•
elektronische Bewegung: ~as
Molekülschwingungen: ~fs
Molekulare Drehbewegung: ~ps
Translationsbewegung: ~ns
Als Folge beeinflussen sich die verschiedenen Bewegungsformen in der Regel
nur wenig und die Wellenfunktion der Kernbewegung kann näherungsweise
separiert werden:
⇥(n) = 't · 'r · 'v
Translation
(2.6.1)
Rotation Vibration
externe
interne
Bewegungsfreiheitsgrade
2.7 Schwingungsbewegung von Molekülen:
Normalkoordinatenanalyse
Theorie → Tafel
Der vibratorische Hamiltonoperator lässt sich in eine Summe von 1Dharmonischen Oszillatoren zerlegen:
3K
3K 
X
X
p
1 2 2
~2 @ 2
+ ! j Yj
Ĥ =
Ĥj =
(2.7.1)
!j =
mit
j
2
2 @Y
2
j=1
j=1
j
Kreisfrequenz
Kraftkonstante
des Oszillators j =Eigenwert der Kraftmatrix
Eigenschaften der Kraftkonstanten λj (=zweite Ableitungen des BO-Potentials
an einem stationären Punkt):
• 5(6) der Kraftkonstanten sind immer ≡0: λF+1= λF+2=...= λ3K=0 (wobei
F=3K-5(6)). Diese entsprechen den externen Bewegungsfreiheitsgraden
Translation und Rotation.
• Wenn alle λ1 = ... = λF >0 handelt es sich um ein lokales Minimum der BO-PF =
stabiles Molekül
• Wenn eine oder mehrere λj<0: stationärer Punkt der BO-PF =
Übergangszustand
Illustration von Minima und Sattelpunkten (Übergangszuständen),
s.a. Abschnitt 2.4.3:
Übergangszustand
(Barriere, Sattelpunkt)
Minimum
(stabiles
Molekül)
Minimum
(stabiles Molekül)
Die vibratorische Schrödingergleichung lässt sich dann in 3K-5(6) 1Dharmonische-Oszillator-Schrödingergleichungen zerlegen: (j=1,2,...,3K-5(6))
2
2
⇤
2 ⇤Yj 2
⇥
1 2 2
+
j Yj ⇥vj (Yj ) = Evj ⇥vj (Yj )
2
(2.7.2)
Lösungen der Schrödingergleichung des 1D-harmonischen Oszillators (s. PC I):
•
Eigenwerte = Schwingungsenergien:
Evj =
j (vj
+ 1/2)
(2.7.3)
mit vj=0,1,2,3,...: vibratorische Quantenzahlen
•
Eigenfunktionen = Schwingungswellenfunktionen:
✓ ◆1
✓r
◆
⇢
4
!
1
!
1! 2
p
Hvj
'vj (Yj ) =
Yj exp
Yj
v
⇡~
~
2~
2 j vj !
(2.7.4)
mit den Hermite-Polynomen Hv(x):
Allgemeiner Ausdruck:
H0 (x) = 1
H1 (x) = 2x
H2 (x) = 4x
v
d
Hv (x) = ( 1)v e
e
v
dx
x2
2
H3 (x) = 8x 3
2
12x
usw.
x2
(2.7.5)
Schwingungswellenfunktionen φv:
v=3
v=2
v=1
v=0
'v
R
|'v |2
Die mit den Normalkoordinaten assoziierten Schwingungsmoden werden auch
als Normalmoden bezeichnet. Beispiele:
•
CO2
(linear: 3.3-5=4 Normalmoden)
symmetrische
Streckschwingung
asymmetrische
Streckschwingung
•
H2O
(gewinkelt: 3.3-6=3 Normalmoden)
symmetrische
Streckschwingung
Biegeschwingung
zwei entartete
Biegeschwingungen
asymmetrische
Streckschwingung
•
C2H4
(3.6-6=12 Normalmoden)
2.8 Drehimpuls in der Quantenmechanik
2.8.1 Definition und Eigenschaften der Drehimpulsoperatoren
Drehimpulsoperatoren sind Bestandteil der Hamiltonoperatoren von vielen
quantenmechanischen Problemen (molekulare Drehbewegung, Stoss- und
Reaktionsprozesse, elektronische Bewegung, etc.). Wir beschäftigen uns also
zunächst mit ihren Eigenschaften und ihrer Matrixdarstellung.
Gemäss dem Korrespondenzprinzip leitt sich der QM Drehimpulsoperator J~ˆ
wie folgt her (siehe auch PC I und II):
2 3 2 3 2 3
Jˆx
p̂x
x̂
J~ˆ = ~rˆ ⇥ p~ˆ , 4Jˆy 5 = 4ŷ 5 ⇥ 4p̂y 5
p̂z
ẑ
Jˆz
Ortsoperator
(2.8.1)
Impulsoperator
mit x̂ = x und p̂x = (~/i )@/@x , analog für die y- und z- Koordinaten.
Auswerten des Vektorprodukts in Gl. (2.8.1) ergibt:
Jˆx = ŷ p̂z ẑ p̂y , Jˆy = ẑ p̂x x̂ p̂z , Jˆz = x̂ p̂y ŷ p̂x
(2.8.2)
Der Operator für das Betragsquadrat des Drehimpulses Ĵ2 (das Quadrat der Länge
des Drehimpulsvektors) ist definiert als:
def
Jˆ2 = J~ˆ · J~ˆ = Jˆx2 + Jˆy2 + Jˆz2
(2.8.3)
Die Drehimpulsoperatoren gehorchen folgenden Vertauschungsrelationen:
def
[Jˆx , Jˆy ] = Jˆx Jˆy
Jˆy Jˆx = i ~Jˆz
bzw.
[Jˆy , Jˆz ] = i ~Jˆx , [Jˆz , Jˆx ] = i ~Jˆy
(2.8.4)
Kommutator
[Jˆ2 , Jˆi ] = 0,
(2.8.5)
i 2 {x, y , z }
wie man leicht aus der Vertauschungsrelationen für die Orts- und Impulsoperatoren
[x̂, p̂x ] = i ~,
[ŷ , p̂y ] = i ~,
[ẑ, p̂z ] = i ~
(2.8.6)
sowie Gl. 2.8.2 herleiten kann. Ausserdem gilt:
[Jˆ2 , Jˆi ] = 0,
(2.8.7)
i 2 {x, y , z }
d.h. Ĵ2 vertauscht mit den Drehimpulskomponenten Ĵx, Ĵy und Ĵz.
Eigenwerte:
Jˆ2 |J, Mi = ~2 J(J + 1)|J, Mi
J=0, 1, 2, ...
(2.8.8)
Jˆz |J, Mi = ~M|J, Mi
M=-J, -J+1, ... , +J
(2.8.9)
Da Ĵx, Ĵy und Ĵz gemäss Gl. (2.8.4) nicht untereinander vertauschen, kann immer nur
eine Komponente des Drehimpulsvektors exakt bestimmt werden. Man wählt
konventionsgemäss Ĵz. Da Ĵ2 und Ĵz gemäss Gl. (2.8.8) vertauschen, können sowohl
die Länge des Drehimpulsvektors als auch seine z-Komponente gleichzeitig exakt
bestimmt werden.
Eigenfunktionen |J, Mi ⌘ YJ,M (✓, ) :
Die Eigenfunktionen der Drehimpulsoperatoren Ĵ2 und Ĵz sind die aus der Lösung
des Wasserstoffatom-Problems bekannten Kugelflächenfunktionen YJ,M(θ,Φ):
J=0
1
2
3
|M|=0
1
2
3
Analytische Ausdrücke:
(2.8.10)
✓ ◆1/2
1
Y0,0 =
4⇡
✓ ◆1/2
3
Y1,0 =
cos(✓)
4⇡
✓ ◆1/2
3
Y1,±1 = ⌥
sin(✓) exp(±i )
8⇡
✓
◆1/2
5
Y2,0 =
3 cos2 (✓) 1
16⇡
✓ ◆1/2
15
Y2,±1 = ⌥
cos(✓) sin(✓) exp(±i ))
8⇡
✓
◆1/2
15
Y2,±2 =
sin2 (✓) exp(±2i ))
32⇡
usw.
2.8.2 Leiteroperatoren
Zum Aufstellen der Matrizen der Drehimpulsoperatoren definiert man nun die
folgenden Leiteroperatoren:
Jˆ+ = Jˆx + i Jˆy
Erzeugungs- (Aufsteige-) Operator
daraus folgt:
Jˆx = 12 (Jˆ+ + Jˆ )
Jˆ = Jˆx
i Jˆy
(2.8.11)
Vernichtungs- (Absteige-) Operator
Jˆy =
Eigenschaften der Leiteroperatoren: → Tafel
1 ˆ
2i (J+
Jˆ )
(2.8.12)
2.8.3 Matrixdarstellung der Drehimpulsoperatoren
Herleitung → Tafel
Zusammenfassung der Matrixelemente der Drehimpulsoperatoren:
hJ, M 0 |Jˆ2 |J, Mi = ~2 J(J + 1)
hJ, M 0 |Jˆz |J, Mi = ~M
hJ, M |Jˆ+ |J, Mi = ~
0
hJ, M |Jˆ |J, Mi = ~
0
hJ, M 0 |Jˆx |J, Mi =
1
2
hJ, M 0 |Jˆy |J, Mi =
1
2i
p
p
(2.8.25)
M 0 ,M
(2.8.24)
M 0 ,M
J(J + 1)
M(M + 1)
M 0 =M+1,M
(2.8.33)
J(J + 1)
M(M
1)
M 0 =M 1,M
(2.8.34)
hJ, M 0 |Jˆ+ |J, Mi + hJ, M 0 |Jˆ |J, Mi
(2.8.35)
hJ, M 0 |Jˆ+ |J, Mi
(2.8.36)
hJ, M 0 |Jˆ |J, Mi
Alle anderen Matrixelemente sind gleich Null.
2.8.4 Kopplung von Drehimpulsen
Wir betrachten zwei Subsysteme mit Drehimpulsen J~1 und J~2 . Diese können zu
einem Gesamtdrehimpuls J~ koppeln.
Bsp.: ein ungepaartes Elektron in einem Atom: Spin-Bahn-Kopplung
(s. Übung 5, PC II):
Basis: |J1 , M1 i ⌘ |`, m` i
• J~1 : Bahndrehimpuls ~` .
• J~2 : Elektronenspin-Drehimpuls ~s .
• J~ : totaler Drehimpuls.
Basis: |J2 , M2 i ⌘ |s, ms i
Basis: |J, Mi
Physikalisch entstehen Drehimpulskopplungen durch die Wechselwirkungen
von magnetischen Momenten, die mit der Drehbeweung von geladenen
Teilchen einhergehen.
Die Kopplung der Drehimpulse impliziert nichts anderes als eine Kopplung der
betreffenden (Dreh)Bewegungen. Drehimpulskopplungen treten immer auf,
sobald mehrere Drehimpulse in einem System vorhanden sind
(Bahndrehimpuls, Spindrehimpuls, Rotationsdrehimpuls, etc.).
Drehimpulskopplungen werden oft mit einem Vektormodell visualisiert. J~ ergibt
sich hierbei aus der Vektorsumme von J~1 und J~2. In Operatorschreibweise:
J~2
J~1
J~ˆ = J~ˆ1 + J~ˆ2
M2
Jˆx = Jˆ1,x + Jˆ2,x
Jˆy = Jˆ1,y + Jˆ2,y
J~
M1
d.h.:
z
(2.8.37)
Jˆz = Jˆ1,z + Jˆ2,z
M
Man betrachtet nun zwei Grenzfälle:
•
Schwache Kopplung zwischen J~1 und J~2 : J~1 , J~2 sind in guter Näherung
unabhängig voneinander (ungekoppelte Darstellung).
Gemeinsame Basis der Drehimpulse: |J1 , M1 , J2 , M2 i = |J1 , M1 i|J2 , M2 i (2.8.38)
•
Starke Kopplung zwischen J~1 und J~2 : J~1 , J~2 sind nicht mehr unabhängig
voneinander (gekoppelte Darstellung).
(2.8.39)
Gemeinsame Basis der Drehimpulse: |J1 , J2 , J, Mi
Die Basen |J1 , M1 , J2 , M2 i und |J1 , J2 , J, Mi sind durch eine Basistransformation
miteinander verbunden:
X
|J1 , J2 , J, Mi =
C(J1 , M1 , J2 , M2 ; J, M) |J1 , M1 , J2 , M2 i
(2.8.40)
M1 ,M2
wobei die Koeffizienten C(J1,M1, J2, M2 ; J, M) Vektorkopplungskoeffizienten
(Clebsch-Gordan (CG)-Koeffizienten) genannt werden. CG-Koeffizienten findet
man in Tabellenwerken.
Bem.: in der Literatur werden CG-Koeffizienten auch oft als sog. Wigner 3JSymbole ausgedrückt:
✓
◆
( 1)J1 J2 M
J1 J2 J
= p
C(J1 , M1 , J2 , M2 ; J, M)
(2.8.41)
M1 M2 J
2J + 1
Wigner 3J-Symbol
CG-Koeffizient
Die möglichen Werte für J ergeben sich aus der Drehimpulserhaltung:
J = J1 + J2 , J1 + J2
1, ..., |J1
J2 |
(Clebsch-Gordan-Reihe)
M = M1 + M2
Beispiele → Tafel, Übung 5 und später in der Vorlesung
(2.8.42)
2.9 Drehbewegung von Molekülen
2.9.1 Schrödingergleichung für die Rotationsbewegung eines Moleküls
Der Hamiltonoperator für die Rotationsbewegung eines
Moleküls wird mittels des Korrespondenzprinzips aus der
klassischen Rotationsenergie Er eines Köpers berechnet:
1
Erot = Ia a2
(2.9.1)
2
Trägheitsmoment
um Rotationsachse a
Winkelgeschwindigkeit
um Rotationsachse a
a
b
Für die freie Rotation im 3D-Raum um die senkrecht stehenden Achsen a,b,c
lautet die Rotationsenergie:
⇥
1
2
2
2
I a a + Ib b + Ic c
Erot =
(2.9.2)
2
Mit der Definition des Drehimpuls Ji=Iiωi (i=a,b,c) erhält man:
⇥
Jb2
Jc2
1 Ja2
+
+
Erot =
2 Ia
Ib
Ic
c
Ersetzt man nun die Drehimpulse Ji durch ihre QM Operatoren Ĵi erhält man den
Hamiltonoperator für die Rotationsbewegung:
⇥
Jˆb2
Jˆc2
Jˆa2
Ĥrot =
+
+
(2.9.3)
2Ia
2Ib
2Ic
... und damit die rotatorische Schrödingergleichung:
⇥
Jˆb2
Jˆc2
Jˆa2
Ĥrot rot =
+
+
rot = Erot rot
2Ia
2Ib
2Ic
(2.9.4)
Die Rotationsachsen a,b,c sind am Molekül fixiert und drehen sich mit diesem
mit. Der molekulare Rotationsdrehimpuls-Operator Ĵ = [Ĵa, Ĵb, Ĵc]T ist also in
diesem molekülfesten, rotierenden Koordinatensystem definiert.
Durch die Transformation in das molekülfeste Koordinatensystem gehorchen die
Komponenten des molekularen Rotations-Drehimpulsoperators “anomalen”
Vertauschungsrelationen mit umgekehrtem Vorzeichnen als in Gl. (2.8.4):
[Jˆa , Jˆb ] =
i ~Jˆc
und zyklische Permutationen
(2.9.5)
Als Folge davon sind Erzeugungs- und Vernichtungsoperator des molekülfesten
Drehimpulses mit entgegengesetztem Vorzeichen im Vergleich zu Gl. (2.8.11)
definiert, s. Übung 4 für Details.
2.9.2 Molekulare Trägheitsmomente
Das Trägheitsmoment Iα für die Rotation eines starren
Körpers bestehend aus K Massenpunkten mi um die
Rotationsachse α ist gegeben durch (s. Physikvorlesung):
I↵ =
K
X
2
mi r↵?,i
(2.9.6)
Normalabstand des Massenpunkts mi
zur Rotationsachse α, α ∈ {a,b,c}
i=1
Die Rotationsachse geht dabei immer durch den
Schwerpunkt S des Moleküls:
1
S = PK
i=1
mi
K
X
i=1
mi ri ,
ri = [xi , yi , zi ]
... kartesische Koordinate des Massenpunktes mi
(2.9.7)
Beispiele (s. auch Übungen):
Nomenklatur: a = Achse mit kleinstem Trägheitsmoment, c = Achse mit grösstem
Trägheitsmoment.
Man klassifiziert Moleküle nach den Eigenschaften ihrer Trägheitsmomente:
•
Sphärische Kreisel: alle Trägheitsmomente sind gleich gross:
I a = Ib = Ic
•
(2.9.8)
Bsp.: CH4, SF6
Symmetrische Kreisel: zwei Trägheitsmomente sind gleich gross:
a) zigarrenförmige symmetrische Kreisel:
Ia < Ib = Ic
(2.9.9)
Bsp.:CH3Cl, CH3CN
b) tellerförmige symmetrische Kreisel:
Ia = Ib < Ic
•
(2.9.10)
Bsp.: NH3, C6H6
Asymmetrische Kreisel: alle Trägheitsmomente verschieden
I a = Ib = Ic
(2.9.11)
Bsp.: alle Moleküle mit niedriger bzw. keiner Symmetrie
Für planare Moleküle gilt:
Ic = Ia + I b
(2.9.12)
2.9.3 Sphärische Kreisel
Für sphärische Kreisel gilt Ia=Ib=Ic≡I. Somit wird die Schrödingergl. (2.9.4) zu:
⇥
Jˆa2 + Jˆb2 + Jˆc2
(2.9.13)
rot = Erot rot
2I
Da das Betragsquadrat des Rotations-Drehimpulsoperators gegeben ist durch:
⇥ˆ 2 = Jˆ2 = Jˆ2 + Jˆ2 + Jˆ2
(2.9.14)
|J|
a
folgt:
Jˆ2
2I
rot
= Erot
b
c
rot
(2.9.15)
Diese Schrödingergleichung ist formal die Eigenwertgleichung des
Drehimpulsoperators Ĵ2, Gl. (2.8.8) ! Die Eigenfunktionen sind somit die
Kugelflächenfunktionen 'rot = YJ,M und die Rotationsenergien sind gegeben
durch:
Jˆ2
Jˆ2
~J(J + 1)
(2.9.16)
'rot =
YJ,M =
YJ,M = Erot YJ,M
2I
2I
2I
also:
mit
und
2
Erot =
2I
J(J + 1)
(2.9.17)
J=0,1,2,...
rotatorische Drehimpulsquantenzahl
M=-J,-J+1,...,+J Quantenzahl der Projektion von J auf die z-Achse
2
Der Ausdruck
B=
2I
(2.9.18)
wird als Rotationskonstante bezeichnet. Ausgedrückt
in Wellenzahlen:
B=
4 cI
(2.9.18)
Damit wird Gl. (4.3.16) zu
Erot (J)/hc = F (J) = BJ(J + 1)
(2.9.19)
Der Abstand zwischen zwei Energieniveaus F(J+1)-F(J) ist
F (J + 1)
F (J) = 2B(J + 1)
(2.9.20)
2.9.4 Symmetrische Kreisel
Für zigarrenförmige Kreisel sind die Trägheitsmomente Ib=Ic>Ia. Man definiert zwei
Rotationskonstanten (in Einheiten von Wellenzahlen):
A=
mit A>B.
4 cIa
und
~
B=
4⇡cIb
(2.9.21)
Rotatorische Energieniveaus
eines spärischen Kreisels
Die Energieniveaus (in Wellenzahlen) sind:
Erot (J, K)/hc = F (J, K) = BJ(J + 1) + (A
B)K
2
(2.9.22)
a
mit einer neuen Quantenzahl K=-J, -J+1, .., J, die der
Projektion von J auf die a-Achse entspricht. Gl. (2.9.22)
wird in Übung 4 hergeitet.
Analog erhält man für tellerförmige Kreisel (Ic>Ia=Ib)
Erot (J, K)/hc = F (J, K) = BJ(J + 1)
(B
C)K 2
(2.9.23)
mit den Rotationskonstanten (in Einheiten von Wellenzahlen):
~
~
B=
C=
(2.9.24)
4⇡cIb
4⇡cIc
Interpretation der
Quantenzahl K
2.9.5 Lineare Kreisel
Lineare Moleküle sind eine Spezialform von
zigarrenförmigen symmetrischen Kreiseln. Da die Kerne als
punktförmig betrachtet werden und alle auf der Molekülachse liegen, ist eine Rotation um diese Achse nicht
möglich: K=0 für lineare Moleküle.
Die Energieniveaus sind wie beim sphärischen Kreisel gegeben durch:
F (J) = BJ(J + 1)
(2.9.25)
a
Zusammenfassung: rotatorische Energieniveaudiagramme
linearer und
sphärischer Kreisel
zigarrenförmiger Kreisel
tellerförmiger Kreisel
Erot
Erot = BJ(J + 1)
Erot = BJ(J + 1) + (A
B)K 2
Erot = BJ(J + 1)
(B
C)K 2
Für asymmetrische Kreisel existiert keine geschlossene Formel für die
Rotationsenergien. Diese müssen in diesem Fall durch Matrixdiagonalisierung
des Hamiltonoperators Gl. (2.9.3) berechnet werden → siehe Übung 4.
2.10 Drehimpuls-Kopplungshierarchien in Molekülen
2.10.1 Drehimpuls-Kopplungshierarchien in Atomen
Wir betrachten ein Atom mit zwei Valenzelektronen mit Bahndrehimpuls ℓ1 und ℓ2
bzw. Elektronenspin-Drehimpuls s1 und s2. Je nach Stärke der Spin-Bahn (SB)Kopplung existieren zwei Grenzfälle für die Drehimpuls-Kopplungshierarchie (s. a.
Übung 5):
•
schwache SB-Kopplung: LS (Russel-Saunders)- Kopplungsschema
1. Die Bahn- und Spindrehimpulse koppeln zunächst zu
Gesamt-Bahndrehimpuls: L = `1 + `2 , `1 + `2
1, ..., |`1
`2 |
(2.10.1)
Gesamt-Spindrehimpuls:
1, ..., |s1
s2 |
(2.10.2)
S = s 1 + s 2 , s1 + s 2
2. L und S koppeln zu einem Gesamt-Drehimpuls J:
J = L + S, L + S
1, ..., |L
S|
(2.10.3)
Die guten (wohldefinierten) Quantenzahlen sind in diesem Fall L,S,J,M
(ungekoppelte Darstellung, s. Abschn. 2.8.4)
•
starke SB-Kopplung: jj- Kopplungsschema
1. Die die individuellen Bahn- und Spindrehimpulse koppeln zuerst:
j1 = `1 + s1 , ..., |`1
s1 |
j2 = `2 + s2 , ..., |`2
s2 |
(2.10.4)
(2.10.5)
2. j1 und j2 koppeln zu einem Gesamt-Drehimpuls J:
J = j1 + j2 , ..., |j1
j2 |
(2.10.6)
Die guten (wohldefinierten) Quantenzahlen sind in diesem
Fall j1,j2,J,M (gekoppelte Darstellung, s. Abschn. 2.8.4)
Je nach Kopplungsschema ergibt sich ein anderes
Energieniveau-Diagramm für das Atom !
Abb.: SB-Kopplung in den Gruppe 14-Elementen (p2
Elektronenknfiguration). Leichte Elemente wie C weisen
schwache SB-Kopplung gemäss dem LS-Kopplungsschema
auf, schwere Elemente wie Pb jj-Kopplung. In letzterem Fall
sind die LS-Termsymbole 2S+1LJ nicht mehr aussagekräftig.
2.10.2 Hundsche Kopplungsfälle
Ähnliche Drehimpuls-Kopplungshierarchien findet man auch in Molekülen:
Hundsche Kopplungsfälle. Wir diskutieren diese für zweiatomige Moleküle, das
Prinzip gilt jedoch ebenso für mehratomige Systeme. Wir visualisieren die beiden
wichtigsten Hunds-Fälle (a und b) mithilfe des Vektormodells der DrehimpulsKopplung.
Hunds-Fall a: starke Kopplung von Elektronen-Bahn- und Spin-Drehimpuls an die
Molekülachse, mittelstarke SB-Wechselwirkung:
Drehimpuls Quantenzahl
J~
~
R
Bedeutung
~
L
L
totaler El. Bahn-DI
~
⇤
Λ
Projektion von L auf Molekülachse
~
S
S
tot. El-Spin-DI
~
⌃
Σ
Projektion von S auf Molekülachse
Kopplungshierarchie:
J~
J
Totaler DI
1.
~
⌦
Ω
Projektion von J auf Molekülachse
~
R
R
Rotations-DI
~
L
~
⇤
~
S
~
⌃
~
⌦
2.
~ =~
~
⌦
⇤+⌃
~ +R
~
J~ = ⌦
(2.10.7)
Gute Quantenz.: J, Ω, Λ, Σ
Notation der molekularen Drehimpulse
Hunds-Fall b: schwache SB-Kopplung, aber der Elektronen-Bahn-Drehimpuls ist
immer noch an die Molekülachse gekoppelt. Tritt überlicherweise in Σ-elektronischen Zuständen (d.h. Λ=0) von zweiatomigen Molekülen sowie üblicherweise in
polyatomigen Molekülen auf.
~
R
~
N
~
S
Kopplungshierarchie:
J~
1.
2.
~
L
~
⇤
~ =~
~
N
⇤+R
~ +S
~
J~ = N
(2.10.8)
Gute Quantenzahlen: J, N, S, Λ
N bezeichnet hier den totalen Drehimpuls ohne Spin. In einem Σ-elektronischen
Zustand (d.h. Λ=0) gilt N≣R.
Zur Erinnerung an PC II: Termsymbole von Molekülen: 2|Σ|+1|Λ|g/u mit:
Beispiel: → Tafel
|Λ|
Symbol
0
Σ
1
Π
2
Δ
3
Φ