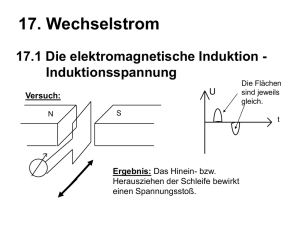
N - sks-weitling.bildung
Werbung
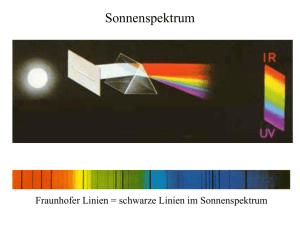
Slide 1
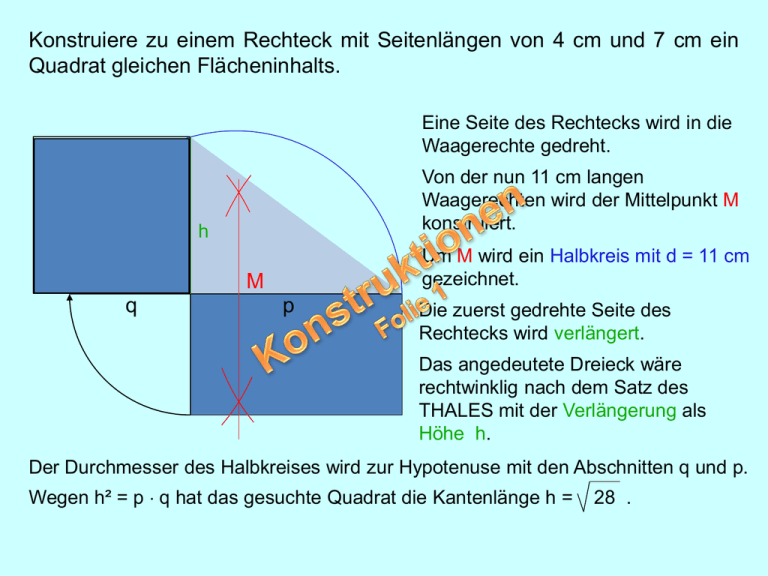
Konstruiere zu einem Rechteck mit Seitenlängen von 4 cm und 7 cm ein
Quadrat gleichen Flächeninhalts.
Eine Seite des Rechtecks wird in die
Waagerechte gedreht.
Von der nun 11 cm langen
Waagerechten wird der Mittelpunkt M
konstruiert.
h
Um M wird ein Halbkreis mit d = 11 cm
gezeichnet.
M
q
p
Die zuerst gedrehte Seite des
Rechtecks wird verlängert.
Das angedeutete Dreieck wäre
rechtwinklig nach dem Satz des
THALES mit der Verlängerung als
Höhe h.
Der Durchmesser des Halbkreises wird zur Hypotenuse mit den Abschnitten q und p.
Wegen h² = p q hat das gesuchte Quadrat die Kantenlänge h =
28 .
Slide 2
Konstruiere Strecken der Länge
2
;
3 ;
5 und
6
cm.
1
1
1
3
1
2
1 cm
5
6
1 cm
Konstruiere eine Strecke der
24 cm.
24
3 cm
Länge
8 cm
Slide 3
Wie groß ist der Flächeninhalt eines Rechtecks, dessen 27,5 cm lange
Diagonalen sich unter einem Winkel von 40,25° schneiden?
e = 27,5 cm
e
180° -
= 40,25°
e
2
e
2
e
2
180° -
e
2
1
e
e
1
e
e
sin
A=
sin (180° 2
2
2
2
2
2
)
Wegen sin = sin (180° - ) sind alle vier Teildreiecke des Rechtecks
gleich groß.
A=
A=4
1
2
e
2
e
1
sin =
2
2
e² sin
A = 244,3156298
A = 244 m²
Slide 4
Der Zahlenwert der Seitenlänge eines Quadrates sei x.
Wie muss x gewählt werden, damit der Zahlenwert des Umfangs bei
entsprechenden Einheiten
a) gleich dem Zahlenwert des Flächeninhalts,
b) größer als der Zahlenwert des Flächeninhalts,
c) kleiner als der Zahlenwert des Flächeninhalts ist?
a)
4x = x²
0 = x² - 4x
x1 = 0
x2 = - p = 4
x=4
b)
4x > x²
0
c)
4x < x²
4
Slide 5
In einem gleichschenkligen Trapez ABCD (AB || CD) halbiert die Diagonale
e den Winkel , während sie den Winkel im Verhältnis 1 : 2 teilt.
a) Wie groß sind die Winkel des Trapezes?
b) Konstruiere ein solches Trapez mit der Seite a = 4,5 cm!
c) Beschreibe die Konstruktion.
D
C
=
a)
x
=
2x
+ = + = 180°
x
x
A
B
b)
D
A
C
Diagonale teilt 1 : 1
Diagonale teilt 1 : 2
= 1,5
+ = + 1,5 = 3,5 = 180°
= 72° =
= 108° =
c) a = 4,5 cm zeichnen; es ergeben sich A und B
in A und in B antragen
w konstruieren; es ergibt sich Punkt C
B
Parallele zu a durch C zeichnen; es
ergibt sich Punkt D
Slide 6
Von einem Dreieck ABC ist bekannt:
(1) Die Seite AB = c ist 25 cm lang.
(2) Die Seitenhalbierende CM = sc ist 12,5 cm lang.
(3) Die Seite BC = a ist 5 cm länger als die Seite AC = b.
Fertige eine entsprechende Skizze an.
Welchen Abstand haben die
C
Punkte A, B und C von M?
Was für ein besonderes
Dreieck ist ABC?
Welche Länge haben die
Seiten a und b?
12,5 cm 25 cm
A
M 12,5 cm
c² = a² + b²
c² = a² + (a - 5)² = a² + a² - 10a + 25
625 = 2a² - 10a + 25
0 = 2a² - 10a - 600
0 = a² - 5a - 300
a = 20 cm
b = 15 cm
B
Welche Flächeninhalt hat
das Dreieck ABC?
1
ab
2
1
A=
20 15
2
A=
A = 150 cm²
Slide 7
Einem Kreis (r = 6,0 cm) ist ein gleichschenkliges Dreieck ABC mit einem
Winkel = 70° an der Spitze einbeschrieben.
Wie lang sind die Seiten des Dreiecks?
70°
C
x
x
sin 70° =
6 cm
70°
x = sin 70° 6 cm
x = 5,64 cm
AB = c = 11,23 cm
140°
55°
55°
A
cos 55° =
B
b
b=
5,64 cm
b
5,64 cm
cos 55°
b = 9,83 cm
55°
5,64 cm
a = 9,83 cm
Slide 8
Berechne die fehlenden Innenwinkel, wenn sich die folgenden Angaben
jeweils auf ein Viereck ABCD beziehen.
a) = 70°; = 80°; = 90°
b) = = 100°; =
c) = = 50°; =
d) + = 180°; = ; = 45°
e) Um welche Arten von Vierecken handelt es sich jeweils in den
Aufgaben a) bis d)?
a)
b)
c)
d)
= 360° - ( + + )
= 360° - (70° + 80° + 90°)
= 120°
+ + + = 360°
+ + + = 360°
2(100° + ) = 360°
= = 80°
+ + + = 360°
+ + + = 360°
2(50° + ) = 360°
= = 130°
= = 135°; = = 45°
e)
allgemeines
Viereck
gleichschenkliges
Trapez
Parallelogramm
Parallelogramm
Slide 9
Gegeben sei ein Kreis mit einer Sehne AB, die nicht durch den Mittelpunkt
des Kreises geht. Ferner seien AC und BD Durchmesser des Kreises.
a) Zeichne eine entsprechende Planfigur und trage die Strecken AD und
BC ein.
b) Bestimme die Größe des Winkels CBA.
Welchen Satz hast du benutzt?
c) Es wird behauptet, dass die Dreiecke ABC und ABD zueinander
kongruent sind.
Führe den Nachweis darüber.
a)
D
b) Winkel CBA = 90°
Satz des THALES
c) ABC ABD Begründung
A
x
M
B
C
AB
AB
ident. Seiten
AC
BD
Durchmesser
CBA BAD nach THALES beide
90°
Zwei Dreiecke sind zueinander
kongruent, wenn sie übereinstimmen in
zwei Seiten und dem der größeren
Seite gegenüberliegenden Winkel.
Slide 10
Konstruiere und beschreibe den Lösungsweg:
Dreieck ABC mit a = 6 cm; = 50°; hc = 2,5 cm
Skizze:
hc
Konstruktion:
C
g1
a
Beschreibung:
1. Gerade g zeichnen; auf ihr soll später
Seite c des Dreiecks liegen; Punkt A
2. Gerade g1 parallel zu g im Abstand von
hc = 2,5 cm zeichnen
3. Winkel = 50° in Punkt A antragen;
Punkt C
4. Kreisbogen mit r = a = 6 cm um C;
Punkt B
5. Punkte B und C verbinden
g
A
B
Slide 11
Konstruiere und beschreibe den Lösungsweg:
Dreieck ABC mit c = 4,5 cm; = 70°; ha = 3,2 cm
Skizze:
Beschreibung:
1. ha zeichnen; Punkt A
2. Gerade g senkrecht durch Fußpunkt von
ha
3. Kreisbogen mit r = c = 4,5 cm um A;
Punkt B
4. Punkte A und B verbinden
5. Winkel = 70° in A antragen; Punkt C
ha
Konstruktion:
c
C
A
B
g
Slide 12
Konstruiere und beschreibe den Lösungsweg:
Dreieck ABC mit a : b = 5 : 3; c = 7 cm; = 60°
Skizze:
a
b
Konstruktion:
c
Beschreibung:
1. Winkel zeichnen; Punkt C
2. Kreisbogen mit r = 5 cm um C; Punkt B‘
3. Kreisbogen mit r = 3 cm um C; Punkt A‘
4. Punkte A‘ und B‘ verbinden
5. Zentrische Streckung (C; k) bis c = 7 cm;
Punkte A und B
C
A‘
B‘
A
B
Slide 13
Von einem Dreieck ABC sind die folgenden Seiten und Winkel gegeben:
AB = c = 5,9 m; BC = a = 4,5 m; BCA = = 74°
a) Berechne die Größe der Winkel und .
b) Konstruiere das Dreieck in einem geeigneten Maßstab! Gib diesen
Maßstab an!
c) Berechne den Flächeninhalt dieses Dreiecks!
Skizze:
a)
sin
a
sin
c
sin
sin =
a
c
Sinussatz
a
b)
sin = 0,7331
C
c
= 47,2°
Maßstab: 1 : 10
5,9m 5,9 cm
a
A
c
=
B
= 58,8°
b) Flächensatz
1
A = 2 ac sin
1
A = 2 4,5 5,9 sin 58,8°
A = 11,4 m²
Slide 14
Konstruiere und beschreibe den Lösungsweg:
Parallelogramm ABCD mit c = 5 cm; d = 3 cm; f = 4 cm
Skizze:
Beschreibung:
1. Seite c = 5 cm zeichnen; Punkte C und D
2. Kreisbogen um C mit r = d = 3 cm
3. Kreisbogen um D mit r = f = 4 cm;
Punkt B
4. Punkte B und C verbinden
5. Strecke BC parallel durch D
C
verschieben; Punkt A
6. Punkte A und B verbinden
c
d
f
Konstruktion:
D
A
B
Slide 15
Konstruiere und beschreibe den Lösungsweg:
Rhombus ABCD mit e = 4 cm; f = 6 cm
Ein ebenes Viereck, bei dem alle vier
Seiten gleich lang sind, heißt Raute (Plural:
Skizze:
Beschreibung:
f
Rauten) oder Rhombus
(Plural: Rhomben).
sind
gegenüberliegende
1. AC= eDabei
= 4 cm
zeichnen;
Punkte A und C
e und gegenüberliegende Winkel gleich groß.
Seiten parallel
2. Mittelsenkrechte von e konstruieren
3. MB = 0,5f = 3 cm zeichnen; Punkt B
4. MD = 0,5f = 3 cm zeichnen; Punkt D
Konstruktion:
5. Punkte ABCD verbinden
D
C
A
M
B
Slide 16
Konstruiere und beschreibe den Lösungsweg:
Viereck ABCD mit a = 5 cm; b = 3,6 cm; c = 6 cm; = 80°; = 115°
Skizze:
Beschreibung:
1. Seite a = 5 cm zeichnen;
Punkte A und B
2. Winkel = 80° in A antragen
3. Winkel = 115° in B antragen
4. Seite b = 3,6 cm auf freiem Schenkel
von abtragen; Punkt C
5. Kreisbogen um C mit r = c = 6 cm;
Punkt D
6. Punkte C und D verbinden
c
b
a
Konstruktion:
D
C
A
B
Slide 17
Die Diagonalen e und f eines beliebigen konvexen Vierecks schneiden
sich unter einem Winkel .
Für den Flächeninhalt des Vierecks
ergibt sich die Formel
A = ½ e f sin
Beweise die Gültigkeit dieser Formel.
sin = sin (180° - )
A1 = ½ ab sin
d
A4
180° -
e
a
A1
A3
c
b f
A2
e=a+c
f=d+d
A2 = ½ bc sin
A3 = ½ cd sin
A4 = ½ da sin
A = A1 + A2 + A3 + A4 = ½ sin (ab + bc + cd + da)
= ½ sin ( b(a + c) + d(c + a) )
= ½ sin ( b(a + c) + d(a + c) )
= ½ sin ( (a + c) (b + d) )
= ½ sin e
f
= ½ e f sin
Slide 18
Gib diejenigen Punktmengen der Ebene (Geraden, Kreise) an, deren
Elemente jeweils eine der folgenden Bedingungen erfüllen.
a) Der Abstand von einem gegebenen Punkt ist gleich.
b) Der Abstand von einer gegebenen Geraden ist gleich.
c) Der Abstand von den Schenkeln eines Winkels ist gleich.
d) Der Abstand von den Endpunkten einer Strecke ist gleich.
e) Der Abstand von zwei gegebenen Parallelen ist gleich.
a) Kreis
b) Parallele zur gegebenen Geraden
c) Winkelhalbierende
d) Mittelsenkrechte der Strecke
e) mittlere Parallele
M
Slide 19
Gegeben sind zwei Parallelen g und h sowie zwei Punkte A und B, die
zwischen den Parallelen liegen. Gesucht ist die Menge der Punkte, die
von den Parallelen gleichen Abstand und von den Punkten A und B
gleiche Entfernung haben.
a) Führe eine solche Konstruktion aus.
b) Gib Bedingungen an, unter denen die Aufgabe
g
- keine Lösung,
m
- genau eine Lösung oder
M
- unendlich viele Lösungen hat.
B
h
n
M
A
a) Von g und h haben alle Punkte auf
b) Keine Lösung:
der mittleren Parallelen m den gleichen
Mittelparallele und -senkrechte
Abstand.
liegen parallel zueinander
Von A und B haben alle Punkte auf der
eine Lösung:
Mittelsenkrechen n von AB die gleiche
unendlich viele Lösungen:
Entfernung.
Mittelparallele und -senkrechte
Ein Punkt der die geforderten Bedingungen
liegen aufeinander
erfüllt liegt dort, wo m und n sich schneiden.
Slide 20
Konstruiere ein rechtwinkliges Dreieck ABC mit BCA = 90°, wenn die
Länge der Seitenhalbierenden sb = 6 cm und CBS = 40° (S ist der
Schnittpunkt von AC mit sb).
Berechne den Umfang und den Flächeninhalt des Dreiecks ABC.
C
Skizze:
Beschreibung:
S
A
Konstruktion:
S
A
sb
40°
C
1. sb = SB = 6 cm zeichnen
B 2. CBS = 40° in B antragen
3. CSB = 180° - (90° + 40°) = 50° in
S antragen; PunktC
4. CS über S hinaus verdoppeln; Punkt A
5. A mit B verbinden
a
sin 50° =
a = 4,60 cm
6 cm
b/2
B
sin 40° =
b/2 = 3,86 cm
6 cm
b = 7,71 cm
c² = a² + b²
c = 8,98 cm
u = a + b + c = 21,3 cm
1
A=
ab = 17,73 cm²
2
Slide 21
Gegeben sind die beiden einander anliegenden
Winkel und mit dem Scheitelpunkt A und dem
Punkt D auf dem gemeinsamen Schenkel.
a) Konstruiere aus dieser Figur ein Dreieck ABC
D
derart, dass AD Seitenhalbierende zu BC ist und A
die Punkte B und C auf verschiedenen
Schenkeln von und liegen, jedoch nicht auf
dem Schenkel, auf dem D liegt.
b) Unter welcher Bedingung wird das Dreieck ABC gleichseitig?
C
a)
C‘
Parallelverschiebung beider Schenkel
A
durch den Punkt D; Punkte B‘ und C‘
Punkte B‘ und C‘ verbinden
B‘C‘ parallel durch Punkt D
D
Verschieben; Punkte B und C
B‘
b) In einem gleichseitigen Dreieck hat jeder Innenwinkel
die Größe von 60°. + = 60°
B
In einem gleichseitigen Dreieck ist die Seitenhalbierende auch die Winkelhalbierende. =
Daraus folgt die Bedingung: = = 30°
Slide 22
Skizze:
Zwei
Straßen schneiden einander im Punkt A.
Durch den Punkt B auf der einen StraßeCwird eine Rohrleitung gelegt, die die
andere Straße im Punkt C schneidet.
Bei der Vermessung wurden folgende Werte ermittelt:
AB = c = 4,7 km;
BAC = = 35°; CBA = = 85°
a) Konstruiere Adas Dreieck ABC in einem
geeigneten Maßstab.
c Abschnittes BC der Rohrleitung.
b) Berechne die Länge a des
B Länge des Abschnittes BC zu
c) Um einen Näherungswert aN für die
erhalten, wurde für CBA = der Näherungswert 90° verwendet. Die Werte
C
für AB = c und BAC = blieben unverändert.
Berechne den Näherungswert aN.
a
d) Gib den absoluten Fehler |aN - a| an!
35°
85°
a) Original 4,7 km Bild 47 mm
47 mm B
A
Bild
47 mm
Maßstab =
=
Original
4700000 mm
aN
tan
35°
=
1
4,7 km
Maßstab =
= 1 : 100000 c)
100000
aN = 3,291 km
35°
b) = 180° - ( 35° + 85°) = 60°
47 mm
B
A
a
4,7
=
sin 35°
sin 60°
d) |3,291 - 3,113| = 0,178 km
a = 3,113 km
Slide 23
Auf einem Betriebsgelände sollen 20 verzinkte Zaungitter (Länge 2,00 m;
Höhe 1,40 m) genutzt werden, um einen Platz mit möglichst großer
Lagerkapazität einzuzäunen.
Man entscheidet sich für eine geeignete Stelle, die durch rechtwinklig
aufeinanderstoßende Mauern ausreichender Länge schon an zwei Seiten
begrenzt ist.
20 m
Mauer
Das Maximum an Fläche bringt ein Quadrat.
10 Gitter je verbleibender Seite.
A = (10 2,00 m)²
A = 400 m²
Slide 24
Ein Vermessungstrupp hat die Länge einer unzugänglichen Strecke AB
trigonometrisch zu bestimmen.
C
A
Er ermittelt die angegebenen
Messwerte.
a) Berechne die Länge der
B
Strecke AB.
b) Auf die gleiche Weise wurde von drei Groppen einer 10. Klasse die
Länge der Strecke AB bestimmt. Sie fanden die folgenden Werte:
Gruppe 1: 73,4 m
a) AB = 45,0² + 72,8² - 2 45,0 72,8 cos 77°
Gruppe 2: 76,4 m
Gruppe 3: 77,3 m
AB = 76,5 m
Berechne den Mittelwert der
b) AB = 1/3 (73,4 + 76,4 + 77,3)
drei Längen.
AB = 75,7 m
c) Um wie viel Meter weicht
dieser Mittelwert von der
c) Abweichung | 75,7 – 76,5 | = 0,8 m
Länge AB, die unter a) berechnet wurde, ab?
Slide 25
Eine neue Eisenbahnlinie wird gebaut. Sie verläuft in einer Ebene
senkrecht zu einer bereits bestehenden Bahnlinie, über die sie mittels
einer Brücke von 8,5 m Höhe geführt werden soll.
Wie lang muss die Rampe mindestens sein, wenn der Anstiegswinkel
nicht mehr als 1° betragen darf?
b
c
a
Einfache Kreuzung
ohne Brücke.
a = 8,5 m
= 1°
Länge der Rampe = c
a
a
tan =
c=
c
tan
8,5
c=
tan 1°
c = 487 m
Slide 26
Von einer Küstenstation K werden zwei Schiffe S1 und S2 geortet, die mit 8
bzw. 5 kn (1 Knoten = 1 Seemeile/h = 1,852 km/h) aufeinander zufahren.
S1 ist in genau nordwestlicher Richtung 16 sm von K und S2 in Richtung
75° von K 27 sm entfernt.
Wann und in welcher Entfernung von K begegnen sich die Schiffe?
s² = 16² + 27² - 2 16 27 cos 120°
s = 37,6 sm
N
S1
45°
s
75°
W
K
v1 t + v2 t = 37,6
8 t + 5 t = 37,6
S2
t = 2,89 h
T
O
t = 2,89 60 min = 173,54 min
t = 2 h 54 min
S1T = 8 sm/h 2,89 h = 23,135 sm
sin
sin 120°
S2T = 5 sm/h 2,89 h = 14,465 sm
= 21,6°
=
16
37,6
Die gesuchte Entfernung
KT² = 27² + 14,465² - 2 27 14,465 cos 21,6°
entspricht der Strecke KT.
KT = 14,5 sm
Slide 27
Ein Küstenmotorschiff fährt mit dem Kurs 159°. Der Schiffsführer peilt
einen Kirchturm in Richtung 90° an. Nach 8 sm Fahrt peilt er denselben
Kirchturm in Richtung 45° an.
Wie weit ist das Schiff bei der letzten Peilung vom Kirchturm entfernt?
gesucht ist die Strecke KS2
S1
90°
159°
69°
69° S2
K
Winkelergänzungen in der Skizze
führen zu allen Innenwinkeln des
Dreiecks S1S2K:
KS1S2 = 159° - 90° = 69°
45°
die 69° ergeben sich als
Wechselwinkel auch bei S2
S1S2K = 90° - 69° + 45° = 66°
S1KS2 = 180° - (66° + 69°) = 45°
KS2
8 sm
=
sin 69°
sin 45°
KS2 = 10,6 sm
Slide 28
Zwei Flugzeuge F1 und F2 starten gleichzeitig vom gleichen Flugplatz. F1
fliegt auf dem Kurs 250° mit einer Geschwindigkeit v1 = 800kmh-1 und F2
auf Kurs 280° mit einer Geschwindigkeit v2 = 900 kmh-1.
Wie weit sind beide Flugzeuge 2 Stunden nach dem Einschwenken auf
den Kurs voneinander entfernt?
Geometrische Lösung:
70° = 250° - 180°
N
Pfeillänge von F1 beträgt
s1 = v1 2 h = 1600 km
80° = 360° - 280°
F2
80°
30° F
F1
Rechnerische Lösung:
Winkelergänzung führt zu
F1FF2 = 30°
70°
Pfeillänge von F2 beträgt
s2 = v2 2 h = 1800 km
Im Maßstab 1 : 40 000 000
sind das 4 cm bzw. 4,5 cm.
Gemessen wird der Abstand von F1
zu F2 mit 2,25 cm.
Das entspricht 900 km.
Damit sind vom F1FF2 zwei Seiten und der von diesen eingeschlossene Winkel
bekannt Kosinussatz:
F1F2 2 = 1600² + 1800² - 2 1600 1800 cos 30°
F1F2 = 900,940 km
Slide 29
Zwecks genauer Standortbestimmung peilt man von einem in Küstennähe
fahrenden Schiff S einen Schornstein T in Richtung N 33,0° O und einen
Leuchtturm L in Richtung N 48,2° W an.
Aus der Seekarte entnimmt man die Strecke LT = 18,3 sm und ihre
Richtung N 82,1° O.
a) Wie weit ist das Schiff vom Leuchtturm entfernt?
b) Welchen Kurs muss das Schiff fahren, um den Leuchtturm im Abstand
N
von 6,5 sm zu passieren?
a) gesucht ist Seite t
N
T
Winkelergänzung führt zu
82,1°
49,1°
L
LST = 48,2° + 33,0°
49,7°
= 81,2°
33,0°
TLS =180° - 82,1° - 48,2°
48,2°
b)
= 49,7°
t
81,2°
STL =180° - 81,2° - 49,7°
= 49,1°
S
6,5 sm
Sinussatz führt zu
sin =
13,997 sm
t
18,3 sm
=
= 27,7° Kurs = 27,7° + 48,2°
sin 49,1°
sin 81,2°
Kurs = N 75,9° W
t = 13,997 sm
Slide 30
Konstruiere zu einem Rechteck mit Seitenlängen von 4 cm und 7 cm ein
Quadrat gleichen Flächeninhalts.
Eine Seite des Rechtecks wird in die
Waagerechte gedreht.
Von der nun 11 cm langen
Waagerechten wird der Mittelpunkt M
konstruiert.
h
Um M wird ein Halbkreis mit d = 11 cm
gezeichnet.
M
q
p
Die zuerst gedrehte Seite des
Rechtecks wird verlängert.
Das angedeutete Dreieck wäre
rechtwinklig nach dem Satz des
THALES mit der Verlängerung als
Höhe h.
Der Durchmesser des Halbkreises wird zur Hypotenuse mit den Abschnitten q und p.
Wegen h² = p q hat das gesuchte Quadrat die Kantenlänge h =
28 .
Slide 2
Konstruiere Strecken der Länge
2
;
3 ;
5 und
6
cm.
1
1
1
3
1
2
1 cm
5
6
1 cm
Konstruiere eine Strecke der
24 cm.
24
3 cm
Länge
8 cm
Slide 3
Wie groß ist der Flächeninhalt eines Rechtecks, dessen 27,5 cm lange
Diagonalen sich unter einem Winkel von 40,25° schneiden?
e = 27,5 cm
e
180° -
= 40,25°
e
2
e
2
e
2
180° -
e
2
1
e
e
1
e
e
sin
A=
sin (180° 2
2
2
2
2
2
)
Wegen sin = sin (180° - ) sind alle vier Teildreiecke des Rechtecks
gleich groß.
A=
A=4
1
2
e
2
e
1
sin =
2
2
e² sin
A = 244,3156298
A = 244 m²
Slide 4
Der Zahlenwert der Seitenlänge eines Quadrates sei x.
Wie muss x gewählt werden, damit der Zahlenwert des Umfangs bei
entsprechenden Einheiten
a) gleich dem Zahlenwert des Flächeninhalts,
b) größer als der Zahlenwert des Flächeninhalts,
c) kleiner als der Zahlenwert des Flächeninhalts ist?
a)
4x = x²
0 = x² - 4x
x1 = 0
x2 = - p = 4
x=4
b)
4x > x²
0
c)
4x < x²
4
Slide 5
In einem gleichschenkligen Trapez ABCD (AB || CD) halbiert die Diagonale
e den Winkel , während sie den Winkel im Verhältnis 1 : 2 teilt.
a) Wie groß sind die Winkel des Trapezes?
b) Konstruiere ein solches Trapez mit der Seite a = 4,5 cm!
c) Beschreibe die Konstruktion.
D
C
=
a)
x
=
2x
+ = + = 180°
x
x
A
B
b)
D
A
C
Diagonale teilt 1 : 1
Diagonale teilt 1 : 2
= 1,5
+ = + 1,5 = 3,5 = 180°
= 72° =
= 108° =
c) a = 4,5 cm zeichnen; es ergeben sich A und B
in A und in B antragen
w konstruieren; es ergibt sich Punkt C
B
Parallele zu a durch C zeichnen; es
ergibt sich Punkt D
Slide 6
Von einem Dreieck ABC ist bekannt:
(1) Die Seite AB = c ist 25 cm lang.
(2) Die Seitenhalbierende CM = sc ist 12,5 cm lang.
(3) Die Seite BC = a ist 5 cm länger als die Seite AC = b.
Fertige eine entsprechende Skizze an.
Welchen Abstand haben die
C
Punkte A, B und C von M?
Was für ein besonderes
Dreieck ist ABC?
Welche Länge haben die
Seiten a und b?
12,5 cm 25 cm
A
M 12,5 cm
c² = a² + b²
c² = a² + (a - 5)² = a² + a² - 10a + 25
625 = 2a² - 10a + 25
0 = 2a² - 10a - 600
0 = a² - 5a - 300
a = 20 cm
b = 15 cm
B
Welche Flächeninhalt hat
das Dreieck ABC?
1
ab
2
1
A=
20 15
2
A=
A = 150 cm²
Slide 7
Einem Kreis (r = 6,0 cm) ist ein gleichschenkliges Dreieck ABC mit einem
Winkel = 70° an der Spitze einbeschrieben.
Wie lang sind die Seiten des Dreiecks?
70°
C
x
x
sin 70° =
6 cm
70°
x = sin 70° 6 cm
x = 5,64 cm
AB = c = 11,23 cm
140°
55°
55°
A
cos 55° =
B
b
b=
5,64 cm
b
5,64 cm
cos 55°
b = 9,83 cm
55°
5,64 cm
a = 9,83 cm
Slide 8
Berechne die fehlenden Innenwinkel, wenn sich die folgenden Angaben
jeweils auf ein Viereck ABCD beziehen.
a) = 70°; = 80°; = 90°
b) = = 100°; =
c) = = 50°; =
d) + = 180°; = ; = 45°
e) Um welche Arten von Vierecken handelt es sich jeweils in den
Aufgaben a) bis d)?
a)
b)
c)
d)
= 360° - ( + + )
= 360° - (70° + 80° + 90°)
= 120°
+ + + = 360°
+ + + = 360°
2(100° + ) = 360°
= = 80°
+ + + = 360°
+ + + = 360°
2(50° + ) = 360°
= = 130°
= = 135°; = = 45°
e)
allgemeines
Viereck
gleichschenkliges
Trapez
Parallelogramm
Parallelogramm
Slide 9
Gegeben sei ein Kreis mit einer Sehne AB, die nicht durch den Mittelpunkt
des Kreises geht. Ferner seien AC und BD Durchmesser des Kreises.
a) Zeichne eine entsprechende Planfigur und trage die Strecken AD und
BC ein.
b) Bestimme die Größe des Winkels CBA.
Welchen Satz hast du benutzt?
c) Es wird behauptet, dass die Dreiecke ABC und ABD zueinander
kongruent sind.
Führe den Nachweis darüber.
a)
D
b) Winkel CBA = 90°
Satz des THALES
c) ABC ABD Begründung
A
x
M
B
C
AB
AB
ident. Seiten
AC
BD
Durchmesser
CBA BAD nach THALES beide
90°
Zwei Dreiecke sind zueinander
kongruent, wenn sie übereinstimmen in
zwei Seiten und dem der größeren
Seite gegenüberliegenden Winkel.
Slide 10
Konstruiere und beschreibe den Lösungsweg:
Dreieck ABC mit a = 6 cm; = 50°; hc = 2,5 cm
Skizze:
hc
Konstruktion:
C
g1
a
Beschreibung:
1. Gerade g zeichnen; auf ihr soll später
Seite c des Dreiecks liegen; Punkt A
2. Gerade g1 parallel zu g im Abstand von
hc = 2,5 cm zeichnen
3. Winkel = 50° in Punkt A antragen;
Punkt C
4. Kreisbogen mit r = a = 6 cm um C;
Punkt B
5. Punkte B und C verbinden
g
A
B
Slide 11
Konstruiere und beschreibe den Lösungsweg:
Dreieck ABC mit c = 4,5 cm; = 70°; ha = 3,2 cm
Skizze:
Beschreibung:
1. ha zeichnen; Punkt A
2. Gerade g senkrecht durch Fußpunkt von
ha
3. Kreisbogen mit r = c = 4,5 cm um A;
Punkt B
4. Punkte A und B verbinden
5. Winkel = 70° in A antragen; Punkt C
ha
Konstruktion:
c
C
A
B
g
Slide 12
Konstruiere und beschreibe den Lösungsweg:
Dreieck ABC mit a : b = 5 : 3; c = 7 cm; = 60°
Skizze:
a
b
Konstruktion:
c
Beschreibung:
1. Winkel zeichnen; Punkt C
2. Kreisbogen mit r = 5 cm um C; Punkt B‘
3. Kreisbogen mit r = 3 cm um C; Punkt A‘
4. Punkte A‘ und B‘ verbinden
5. Zentrische Streckung (C; k) bis c = 7 cm;
Punkte A und B
C
A‘
B‘
A
B
Slide 13
Von einem Dreieck ABC sind die folgenden Seiten und Winkel gegeben:
AB = c = 5,9 m; BC = a = 4,5 m; BCA = = 74°
a) Berechne die Größe der Winkel und .
b) Konstruiere das Dreieck in einem geeigneten Maßstab! Gib diesen
Maßstab an!
c) Berechne den Flächeninhalt dieses Dreiecks!
Skizze:
a)
sin
a
sin
c
sin
sin =
a
c
Sinussatz
a
b)
sin = 0,7331
C
c
= 47,2°
Maßstab: 1 : 10
5,9m 5,9 cm
a
A
c
=
B
= 58,8°
b) Flächensatz
1
A = 2 ac sin
1
A = 2 4,5 5,9 sin 58,8°
A = 11,4 m²
Slide 14
Konstruiere und beschreibe den Lösungsweg:
Parallelogramm ABCD mit c = 5 cm; d = 3 cm; f = 4 cm
Skizze:
Beschreibung:
1. Seite c = 5 cm zeichnen; Punkte C und D
2. Kreisbogen um C mit r = d = 3 cm
3. Kreisbogen um D mit r = f = 4 cm;
Punkt B
4. Punkte B und C verbinden
5. Strecke BC parallel durch D
C
verschieben; Punkt A
6. Punkte A und B verbinden
c
d
f
Konstruktion:
D
A
B
Slide 15
Konstruiere und beschreibe den Lösungsweg:
Rhombus ABCD mit e = 4 cm; f = 6 cm
Ein ebenes Viereck, bei dem alle vier
Seiten gleich lang sind, heißt Raute (Plural:
Skizze:
Beschreibung:
f
Rauten) oder Rhombus
(Plural: Rhomben).
sind
gegenüberliegende
1. AC= eDabei
= 4 cm
zeichnen;
Punkte A und C
e und gegenüberliegende Winkel gleich groß.
Seiten parallel
2. Mittelsenkrechte von e konstruieren
3. MB = 0,5f = 3 cm zeichnen; Punkt B
4. MD = 0,5f = 3 cm zeichnen; Punkt D
Konstruktion:
5. Punkte ABCD verbinden
D
C
A
M
B
Slide 16
Konstruiere und beschreibe den Lösungsweg:
Viereck ABCD mit a = 5 cm; b = 3,6 cm; c = 6 cm; = 80°; = 115°
Skizze:
Beschreibung:
1. Seite a = 5 cm zeichnen;
Punkte A und B
2. Winkel = 80° in A antragen
3. Winkel = 115° in B antragen
4. Seite b = 3,6 cm auf freiem Schenkel
von abtragen; Punkt C
5. Kreisbogen um C mit r = c = 6 cm;
Punkt D
6. Punkte C und D verbinden
c
b
a
Konstruktion:
D
C
A
B
Slide 17
Die Diagonalen e und f eines beliebigen konvexen Vierecks schneiden
sich unter einem Winkel .
Für den Flächeninhalt des Vierecks
ergibt sich die Formel
A = ½ e f sin
Beweise die Gültigkeit dieser Formel.
sin = sin (180° - )
A1 = ½ ab sin
d
A4
180° -
e
a
A1
A3
c
b f
A2
e=a+c
f=d+d
A2 = ½ bc sin
A3 = ½ cd sin
A4 = ½ da sin
A = A1 + A2 + A3 + A4 = ½ sin (ab + bc + cd + da)
= ½ sin ( b(a + c) + d(c + a) )
= ½ sin ( b(a + c) + d(a + c) )
= ½ sin ( (a + c) (b + d) )
= ½ sin e
f
= ½ e f sin
Slide 18
Gib diejenigen Punktmengen der Ebene (Geraden, Kreise) an, deren
Elemente jeweils eine der folgenden Bedingungen erfüllen.
a) Der Abstand von einem gegebenen Punkt ist gleich.
b) Der Abstand von einer gegebenen Geraden ist gleich.
c) Der Abstand von den Schenkeln eines Winkels ist gleich.
d) Der Abstand von den Endpunkten einer Strecke ist gleich.
e) Der Abstand von zwei gegebenen Parallelen ist gleich.
a) Kreis
b) Parallele zur gegebenen Geraden
c) Winkelhalbierende
d) Mittelsenkrechte der Strecke
e) mittlere Parallele
M
Slide 19
Gegeben sind zwei Parallelen g und h sowie zwei Punkte A und B, die
zwischen den Parallelen liegen. Gesucht ist die Menge der Punkte, die
von den Parallelen gleichen Abstand und von den Punkten A und B
gleiche Entfernung haben.
a) Führe eine solche Konstruktion aus.
b) Gib Bedingungen an, unter denen die Aufgabe
g
- keine Lösung,
m
- genau eine Lösung oder
M
- unendlich viele Lösungen hat.
B
h
n
M
A
a) Von g und h haben alle Punkte auf
b) Keine Lösung:
der mittleren Parallelen m den gleichen
Mittelparallele und -senkrechte
Abstand.
liegen parallel zueinander
Von A und B haben alle Punkte auf der
eine Lösung:
Mittelsenkrechen n von AB die gleiche
unendlich viele Lösungen:
Entfernung.
Mittelparallele und -senkrechte
Ein Punkt der die geforderten Bedingungen
liegen aufeinander
erfüllt liegt dort, wo m und n sich schneiden.
Slide 20
Konstruiere ein rechtwinkliges Dreieck ABC mit BCA = 90°, wenn die
Länge der Seitenhalbierenden sb = 6 cm und CBS = 40° (S ist der
Schnittpunkt von AC mit sb).
Berechne den Umfang und den Flächeninhalt des Dreiecks ABC.
C
Skizze:
Beschreibung:
S
A
Konstruktion:
S
A
sb
40°
C
1. sb = SB = 6 cm zeichnen
B 2. CBS = 40° in B antragen
3. CSB = 180° - (90° + 40°) = 50° in
S antragen; PunktC
4. CS über S hinaus verdoppeln; Punkt A
5. A mit B verbinden
a
sin 50° =
a = 4,60 cm
6 cm
b/2
B
sin 40° =
b/2 = 3,86 cm
6 cm
b = 7,71 cm
c² = a² + b²
c = 8,98 cm
u = a + b + c = 21,3 cm
1
A=
ab = 17,73 cm²
2
Slide 21
Gegeben sind die beiden einander anliegenden
Winkel und mit dem Scheitelpunkt A und dem
Punkt D auf dem gemeinsamen Schenkel.
a) Konstruiere aus dieser Figur ein Dreieck ABC
D
derart, dass AD Seitenhalbierende zu BC ist und A
die Punkte B und C auf verschiedenen
Schenkeln von und liegen, jedoch nicht auf
dem Schenkel, auf dem D liegt.
b) Unter welcher Bedingung wird das Dreieck ABC gleichseitig?
C
a)
C‘
Parallelverschiebung beider Schenkel
A
durch den Punkt D; Punkte B‘ und C‘
Punkte B‘ und C‘ verbinden
B‘C‘ parallel durch Punkt D
D
Verschieben; Punkte B und C
B‘
b) In einem gleichseitigen Dreieck hat jeder Innenwinkel
die Größe von 60°. + = 60°
B
In einem gleichseitigen Dreieck ist die Seitenhalbierende auch die Winkelhalbierende. =
Daraus folgt die Bedingung: = = 30°
Slide 22
Skizze:
Zwei
Straßen schneiden einander im Punkt A.
Durch den Punkt B auf der einen StraßeCwird eine Rohrleitung gelegt, die die
andere Straße im Punkt C schneidet.
Bei der Vermessung wurden folgende Werte ermittelt:
AB = c = 4,7 km;
BAC = = 35°; CBA = = 85°
a) Konstruiere Adas Dreieck ABC in einem
geeigneten Maßstab.
c Abschnittes BC der Rohrleitung.
b) Berechne die Länge a des
B Länge des Abschnittes BC zu
c) Um einen Näherungswert aN für die
erhalten, wurde für CBA = der Näherungswert 90° verwendet. Die Werte
C
für AB = c und BAC = blieben unverändert.
Berechne den Näherungswert aN.
a
d) Gib den absoluten Fehler |aN - a| an!
35°
85°
a) Original 4,7 km Bild 47 mm
47 mm B
A
Bild
47 mm
Maßstab =
=
Original
4700000 mm
aN
tan
35°
=
1
4,7 km
Maßstab =
= 1 : 100000 c)
100000
aN = 3,291 km
35°
b) = 180° - ( 35° + 85°) = 60°
47 mm
B
A
a
4,7
=
sin 35°
sin 60°
d) |3,291 - 3,113| = 0,178 km
a = 3,113 km
Slide 23
Auf einem Betriebsgelände sollen 20 verzinkte Zaungitter (Länge 2,00 m;
Höhe 1,40 m) genutzt werden, um einen Platz mit möglichst großer
Lagerkapazität einzuzäunen.
Man entscheidet sich für eine geeignete Stelle, die durch rechtwinklig
aufeinanderstoßende Mauern ausreichender Länge schon an zwei Seiten
begrenzt ist.
20 m
Mauer
Das Maximum an Fläche bringt ein Quadrat.
10 Gitter je verbleibender Seite.
A = (10 2,00 m)²
A = 400 m²
Slide 24
Ein Vermessungstrupp hat die Länge einer unzugänglichen Strecke AB
trigonometrisch zu bestimmen.
C
A
Er ermittelt die angegebenen
Messwerte.
a) Berechne die Länge der
B
Strecke AB.
b) Auf die gleiche Weise wurde von drei Groppen einer 10. Klasse die
Länge der Strecke AB bestimmt. Sie fanden die folgenden Werte:
Gruppe 1: 73,4 m
a) AB = 45,0² + 72,8² - 2 45,0 72,8 cos 77°
Gruppe 2: 76,4 m
Gruppe 3: 77,3 m
AB = 76,5 m
Berechne den Mittelwert der
b) AB = 1/3 (73,4 + 76,4 + 77,3)
drei Längen.
AB = 75,7 m
c) Um wie viel Meter weicht
dieser Mittelwert von der
c) Abweichung | 75,7 – 76,5 | = 0,8 m
Länge AB, die unter a) berechnet wurde, ab?
Slide 25
Eine neue Eisenbahnlinie wird gebaut. Sie verläuft in einer Ebene
senkrecht zu einer bereits bestehenden Bahnlinie, über die sie mittels
einer Brücke von 8,5 m Höhe geführt werden soll.
Wie lang muss die Rampe mindestens sein, wenn der Anstiegswinkel
nicht mehr als 1° betragen darf?
b
c
a
Einfache Kreuzung
ohne Brücke.
a = 8,5 m
= 1°
Länge der Rampe = c
a
a
tan =
c=
c
tan
8,5
c=
tan 1°
c = 487 m
Slide 26
Von einer Küstenstation K werden zwei Schiffe S1 und S2 geortet, die mit 8
bzw. 5 kn (1 Knoten = 1 Seemeile/h = 1,852 km/h) aufeinander zufahren.
S1 ist in genau nordwestlicher Richtung 16 sm von K und S2 in Richtung
75° von K 27 sm entfernt.
Wann und in welcher Entfernung von K begegnen sich die Schiffe?
s² = 16² + 27² - 2 16 27 cos 120°
s = 37,6 sm
N
S1
45°
s
75°
W
K
v1 t + v2 t = 37,6
8 t + 5 t = 37,6
S2
t = 2,89 h
T
O
t = 2,89 60 min = 173,54 min
t = 2 h 54 min
S1T = 8 sm/h 2,89 h = 23,135 sm
sin
sin 120°
S2T = 5 sm/h 2,89 h = 14,465 sm
= 21,6°
=
16
37,6
Die gesuchte Entfernung
KT² = 27² + 14,465² - 2 27 14,465 cos 21,6°
entspricht der Strecke KT.
KT = 14,5 sm
Slide 27
Ein Küstenmotorschiff fährt mit dem Kurs 159°. Der Schiffsführer peilt
einen Kirchturm in Richtung 90° an. Nach 8 sm Fahrt peilt er denselben
Kirchturm in Richtung 45° an.
Wie weit ist das Schiff bei der letzten Peilung vom Kirchturm entfernt?
gesucht ist die Strecke KS2
S1
90°
159°
69°
69° S2
K
Winkelergänzungen in der Skizze
führen zu allen Innenwinkeln des
Dreiecks S1S2K:
KS1S2 = 159° - 90° = 69°
45°
die 69° ergeben sich als
Wechselwinkel auch bei S2
S1S2K = 90° - 69° + 45° = 66°
S1KS2 = 180° - (66° + 69°) = 45°
KS2
8 sm
=
sin 69°
sin 45°
KS2 = 10,6 sm
Slide 28
Zwei Flugzeuge F1 und F2 starten gleichzeitig vom gleichen Flugplatz. F1
fliegt auf dem Kurs 250° mit einer Geschwindigkeit v1 = 800kmh-1 und F2
auf Kurs 280° mit einer Geschwindigkeit v2 = 900 kmh-1.
Wie weit sind beide Flugzeuge 2 Stunden nach dem Einschwenken auf
den Kurs voneinander entfernt?
Geometrische Lösung:
70° = 250° - 180°
N
Pfeillänge von F1 beträgt
s1 = v1 2 h = 1600 km
80° = 360° - 280°
F2
80°
30° F
F1
Rechnerische Lösung:
Winkelergänzung führt zu
F1FF2 = 30°
70°
Pfeillänge von F2 beträgt
s2 = v2 2 h = 1800 km
Im Maßstab 1 : 40 000 000
sind das 4 cm bzw. 4,5 cm.
Gemessen wird der Abstand von F1
zu F2 mit 2,25 cm.
Das entspricht 900 km.
Damit sind vom F1FF2 zwei Seiten und der von diesen eingeschlossene Winkel
bekannt Kosinussatz:
F1F2 2 = 1600² + 1800² - 2 1600 1800 cos 30°
F1F2 = 900,940 km
Slide 29
Zwecks genauer Standortbestimmung peilt man von einem in Küstennähe
fahrenden Schiff S einen Schornstein T in Richtung N 33,0° O und einen
Leuchtturm L in Richtung N 48,2° W an.
Aus der Seekarte entnimmt man die Strecke LT = 18,3 sm und ihre
Richtung N 82,1° O.
a) Wie weit ist das Schiff vom Leuchtturm entfernt?
b) Welchen Kurs muss das Schiff fahren, um den Leuchtturm im Abstand
N
von 6,5 sm zu passieren?
a) gesucht ist Seite t
N
T
Winkelergänzung führt zu
82,1°
49,1°
L
LST = 48,2° + 33,0°
49,7°
= 81,2°
33,0°
TLS =180° - 82,1° - 48,2°
48,2°
b)
= 49,7°
t
81,2°
STL =180° - 81,2° - 49,7°
= 49,1°
S
6,5 sm
Sinussatz führt zu
sin =
13,997 sm
t
18,3 sm
=
= 27,7° Kurs = 27,7° + 48,2°
sin 49,1°
sin 81,2°
Kurs = N 75,9° W
t = 13,997 sm
Slide 30