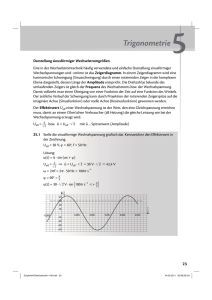
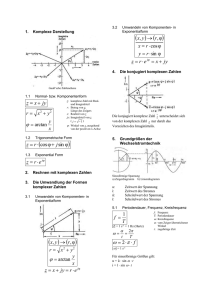
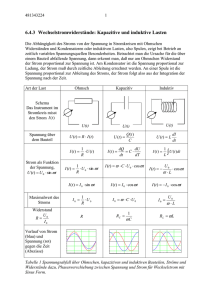
Zeigerdiagramme

1
Das Zeigerdiagramm für Wechselspannung mit Sinus Form
Der Wert der Spannung U (t )  U 0  sin t ist durch ihren Betrag U0 und die „Phase“ t gegeben. Beide Informationen kann man in einen „Zeiger“ verpacken. Betrag und Phase sind dann
als Länge des Vektors und als Winkel zur x  Achse, der „reellen Achse“, unmittelbar ablesbar:
Imaginäre Achse
U 0  sin t
Reelle Achse
Phasenwinkel
t
Abbildung 1 Zeigerdiagramm in der komplexen Ebene
Die zeitliche Änderung der so dargestellten Größen entspricht der Drehung des Zeigers mit
konstanter Winkelgeschwindigkeit. Die trigonometrische Formulierung entspricht dann der
Projektion des Zeigers auf eine der Achsen. http://www.unituebingen.de/uni/pki/skripten/V4_2Wellen.DOC - Kreisbewegungen
Komplexe Schreibweise für Spannung, Ströme und Widerstände
Die mathematische Entsprechung des Zeigers in der komplexen Ebene ist die komplexe Exponentialfunktion. Die Verbindung zur trigonometrischen Formulierung liefert die Eulersche
Formel:
Schreibweise
Komplex
i
Trigonometrisch
sin 
e  cos   i  sin 
Eulersche Formel
Anwendung, z. B. auf die
U 0  sin t 
U  U 0  e it
Elektrische Spannung:
Tabelle 1 Eulersche Formel und Exponential-Schreibweise der Wechselspannung. Als trigonometrische Schreibweise kann auch der Realteil ausgewählt werden..
Spannung ist mit dem Strom nach dem Ohmschen Gesetz U  R  I verknüpft. Bei kapazitiven und induktiven Widerständen unterscheidet sich der Strom nicht nur im Betrag, sondern
auch in der Phase von der Spannung. Um das Ohmsche Gesetz formal beizubehalten, werden
auch im Widerstand zwei Informationen verpackt, deshalb wird auch er als komplexe Zahl in
geschrieben. Der Betrag des Widerstands ist der reelle Faktor vor der Exponentialfunktion,
die Phase wird aus dem Exponenten als reeller Faktor von i unmittelbar abgelesen.
Die Eulerschen Formel zeigt, daß ein Faktor i im Ergebnis zu einer Phasenverschiebung um
 2 äquivalent ist:
2
Realteil
Imaginärteil
0
1


cost  
2



sin t  
2

Der Faktor i entspricht dem Zeiger mit Betrag 1 und Phase
 2:
i  cos

 i  sin
2

2
e
i

2
Multiplikation von e it mit  i entspricht einer Phasenverschiebung um  2 :
ie
it
e
i

2
e
i t
e


i t  
2

Berechnung der Widerstände
Art der Last
Ohmsch
Kapazitiv
U(t)
U(t)
Induktiv
Schema
Spannung über
dem Bauteil
U (t )  R  I (t )
Strom als Funktion der Spannung,
U (t )  U 0  e it
eingesetzt:
Strom als Funktion der Spannung,
U (t )  U 0  e it
eingesetzt:
I (t ) 
I (t ) 
1
 U (t )
R
1
 U 0  e it
R
I (t ) 
Widerstand
U (t )
R
I (t )
U (t ) 
1
 U (t )
R
Q(t )
C
U (t )  L
I (t )  Q  C  U
I (t )  C  U 0 
I (t ) 
 
d it
e
dt
I (t )  i    C  U (t )
RC  
R
i
Zeigerdiagramm für
den Widerstand
U(t)
1
U (t )dt
L
U0
  e it dt
L
I (t )  
i
C
i
U (t )
L
R L  iL
i
r
I (t ) 
dI
dt
i
r
r
3
Zeigerdiagramm für
Strom (blau)
und Spannung
(orange) und
Verlauf beider
Größen gegen
die Zeit
(Abszisse)
F1
F2
1,0
1,0
0,5
0,5
0,5
0,0
Y Axis Title
1,0
Y Axis Title
Y Axis Title
F1
F2
0,0
-1,0
-1,0
-1,0
0
2
4
6
8
0
10
0,0
-0,5
-0,5
-0,5
F1
F2
2
4
6
8
10
0
2
4
6
8
10
X Axis Title
X Axis Title
X Axis Title
Tabelle 2 Phasenverschiebung zwischen Spannung und Strom für Ohmsche, kapazitive und
induktive Lasten bei Betrieb mit Wechselstrom mit Sinus Form.
Der Faktor  i zwischen Strom und Spannung zeigt eine Phasenverschiebung von  90 0 :
Für den Kondensator und die Spule gilt deshalb:
Schreibweise
Vektor in der komplexen Ebene
U (t )  U 0  e it
Spannung:
Strom im Kondensator:
I (t )  i   C  U (t )  I 0  e

Strom in der Spule:
I (t ) 


i  t  
2

Trigonometrisch
U 0  sin t 


I 0  sin t  
2



I 0  sin t  
2


i  t  
i
 U (t )  I 0  e  2 
 L
Tabelle 3 Phasenverschiebung des Stroms gegen die Spannung beim kapazitiven und induktiven Widerstand
Auch die komplexen Widerstände können vektoriell, als Zeigerdiagramm dargestellt werden.
Zur Berechnung des Gesamtwiderstands ihrer Kombinationen werden die Widerstände vektoriell addiert. Die durch die Widerstände verursachte Phasenverschiebung zwischen Strom und
Spannung ist als Winkel der Vektoren zur waagrechten, reellen Achse unmittelbar abzulesen:
Vorteil dieser Darstellung!
L
L
R
R
1
C
1
C
R  iL  i
Abbildung 2 Zeigerdiagramm von Wechselstromwiderständen und ihrer Summe
1
C