Lk Physik Aufgabenblatt März Wechselstromwiderstände 1

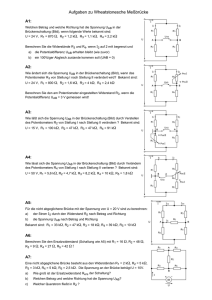
Lk Physik
Aufgabenblatt
März
Wechselstromwiderstände
1. Gegeben ist nebenstehende Schaltung mit
1
R1 = R2 = 5 Ω und
= 6 Ω.
ωC
Der Scheitelwert der Wechselspannung ist so groß,
dass
UBC0 = 10 V ist.
Die Scheitelwerte der Größen werden hier durch den
Index 0 gekennzeichnet.
IC
Aq R1 Bq q
IR
C
R2
q Cq
I
U = U0 · cos(ωt)
bb
a) Legen Sie ein Zeigerdiagramm für die gesamte Schaltung an.
Gehen Sie dabei von der Teilspannung UBC0 aus, die Sie waagerecht einzeichnen.
b) Berechnen Sie den Gesamtstrom I0 und seine Phasenverschiebung ∆α zur Spannung UBC0 .
c) Berechnen Sie nun aus UAB0 und UBC0 die Gesamtspannung U0 und ihre Phasenverschiebung ∆β zur Spannung UBC0 .
Zerlegen Sie zur Durchführung der Vektoraddition die Vektoren in ihre waagerechten
und senkrechten Komponenten.
d) Aus ∆α und ∆β können Sie nun die Phasenverschiebung ∆ϕ zwischen U und I
ermitteln.
e) Berechnen Sie nun den Wechselstromwiderstand X der gesamten Anordnung.
f) Wie groß müsste die Spannung UBC0 gewählt werden, damit die Gesamtspannung U0 = 15 V ist ?
Viel Erfolg !
Kink
Lk Physik
Musterlösung
Wechselstromwiderstände
1.
a) Zeigerdiagramm :
Im 6
IC 6
7I
UAB7
∆ϕ
∆β
∆α IR UBC
1U
-
Re
UBC0
R
UBC0
ICO =
= UBC0 ωC
1
ωC
s
s
2
p
U
1
BC0
2
2 2
2 + I2 =
IO = IRO
+ ω2C 2
CO
2 + UBC0 ω C = UBC0
R
R2
s
1
1
= 10 V
= 2,6 A
2+
25 Ω
36 Ω2
b) IRO =
IC0
5
= RωC =
IR0
6
◦
⇒ ∆α = 40
tan ∆α =
c) UAB0 = R1 · I0 = 5 Ω · 2,6 A = 13 V
d) Re(UAB ) = UAB0 · cos ∆α = 13 v · cos 40 ◦ = 10 V
Im(UAB ) = UAB0 · sin ∆α = 13 v · sin 40 ◦ = 8,4 V
Re(U ) = Re(UAB ) + UBC = 10 V + 10 V = 20 V
Im(U ) = Im(UAB ) = 8,4 V
p
p
U0 = Re(U )2 + Im(U )2 = 202 V2 + 8,42 V2 = 22 V
tan ∆β =
Im(U ) 8,4 V
=
= 0,42
Re(U )
20 V
⇒ ∆β = 23 ◦
∆ϕ = ∆α − ∆β = 40 ◦ − 23 ◦ = 17 ◦
e) X =
Ueff U0
22 V
=
=
= 8, 5 Ω
Ieff
I0
2,6 A
0
f) UBC0 : UBC0
= U0 : U00
U00
15 V
0
= 10 V ·
= 6, 8 V
UBC0 = UBC0 ·
U0
22 V
März