7. Impuls, Drehimpuls und Energie 1. Der Körper wird aus dem

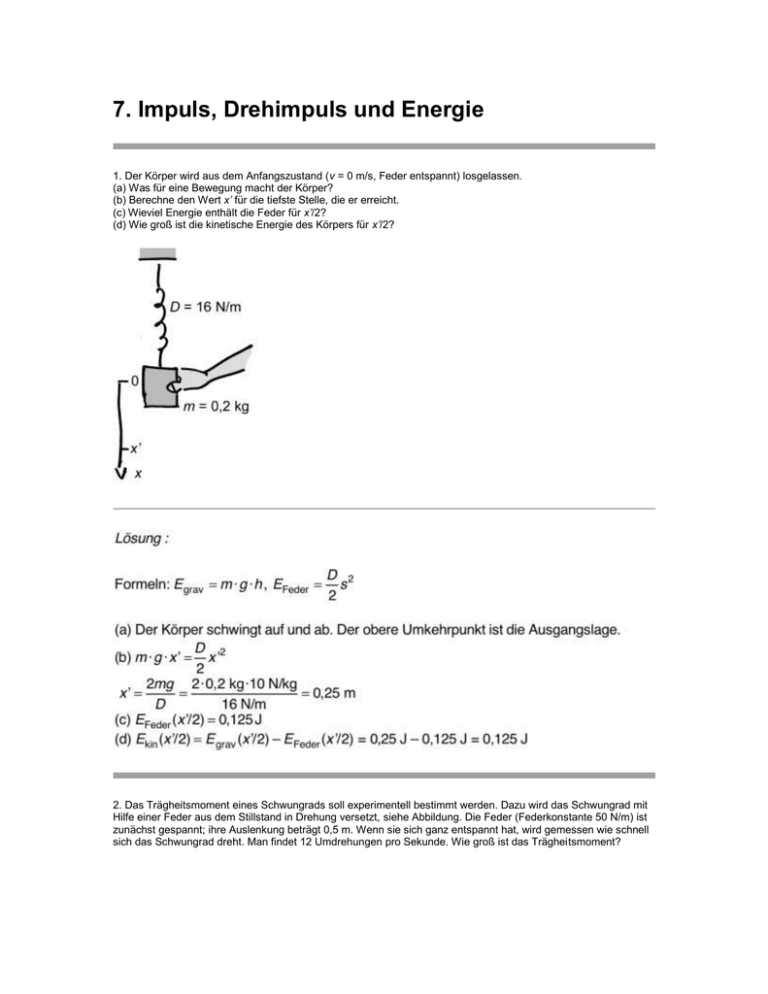
7. Impuls, Drehimpuls und Energie
1. Der Körper wird aus dem Anfangszustand (v = 0 m/s, Feder entspannt) losgelassen.
(a) Was für eine Bewegung macht der Körper?
(b) Berechne den Wert x’ für die tiefste Stelle, die er erreicht.
(c) Wieviel Energie enthält die Feder für x’/2?
(d) Wie groß ist die kinetische Energie des Körpers für x’/2?
2. Das Trägheitsmoment eines Schwungrads soll experimentell bestimmt werden. Dazu wird das Schwungrad mit
Hilfe einer Feder aus dem Stillstand in Drehung versetzt, siehe Abbildung. Die Feder (Federkonstante 50 N/m) ist
zunächst gespannt; ihre Auslenkung beträgt 0,5 m. Wenn sie sich ganz entspannt hat, wird gemessen wie schnell
sich das Schwungrad dreht. Man findet 12 Umdrehungen pro Sekunde. Wie groß ist das Trägheitsmoment?
3. Das Trägheitsmoment eines Schwungrads soll experimentell bestimmt werden. Dazu wird das Schwungrad mit
Hilfe eines Gewichts aus dem Stillstand in Drehung versetzt. Wenn sich das Gewicht um 1m gesenkt hat, dreht
sich das Schwungrad mit drei Umdrehungen pro Sekunde.
4. Rheinkraftwerk Iffezheim:
Hohenunterschied 11 Meter
Wasserstrom 750 Kubikmeter pro Sekunde
Wie viel elektrische Energie kann produziert werden?
5. Ein Pumpspeicherwerk hat ein „Oberbecken“ auf 800 m Höhe und ein „Unterbecken“ auf 400 m Höhe.
(a) Wie groß ist das Gravitationspotenzial oben und unten (bezogen auf NN)?
(b) Die nutzbare Wassermenge geträgt 8 Millionen Kubikmeter. Wie viel Energie kann gespeichert werden?
(c) Die Generatoren liefern einen Energiestrom von maximal 800 MW. Wie lange reicht der Energievorrat?
6. Ein Gleiter auf der Luftkissenbahn stößt gegen einen doppelt so schweren, der sich am Anfang nicht bewegt.
Der Stoß ist völlig unelastisch (Puffer aus Knetmasse). Vergleiche die kinetische Energie vor dem Stoß mit der
nach dem Stoß. Erkläre.
7. Zwei Schwungräder A und B haben je ein Trägheitsmoment von
Winkelgeschwindigkeit von
. A dreht sich mit einer
, B dreht sich nicht.
(a) Welchen Drehimpuls hat Rad A?
(b) Welche Energie hat A auf Grund seiner Drehung?
Die Räder werden nun mit Hilfe einer Rutschkupplung miteinander verbunden.
(c) Wie viel Drehimpuls hat jetzt jedes der beiden Räder?
(d) Wie viel Energie hat jedes Rad? Wie viel Energie haben beide zusammen?
(e) Vergleiche mit dem Ergebnis von (b) und kommentiere.
8. Es gibt eine Analogie zwischen geradlinigen Bewegungen und Drehbewegungen. Welche physikalischen
Größen entsprechen sich? Welche Formeln entsprechen sich?
Lösung:
9. (a) Seil E bewegt sich mit 0,2 m/s. Welche Geschwindigkeiten haben die Seilstücke B und C?
(b) Wie sind die Impulsströme an den Stellen A, B, C, D und E?
(c) Wie sind die Energieströme an den Stellen A, B, C, D und E?
(d) Welchen Weg nimmt der Energiestrom?
(e) Die Last wird um 2 m gehoben. Wieviel Energie muss das Männchen liefern?
Lösung:
10. Ein 30 kg schwerer Wagen wird mit Impuls geladen. Es fließt 6 Sekunden lang ein Impulsstrom von 20 N. Es
gibt keine Reibungsverluste. Welche kinetische Energie hat der Wagen am Ende?
11. Ein Wagen (m = 20 kg) fährt mit v = 0,5 m/s in x-Richtung gegen einen Federpuffer und prallt zurück.
(a) Wie ist sein Impuls vor und nach dem Stoß?
(b) Wie ist seine kinetische Energie vor und nach dem Stoß?
(c) Wie stark wird die Feder zusammengedrückt? (Federkonstante D = 60 N/m)
(d) Wie groß ist die Geschwindigkeit des Wagens, wenn die Feder gerade zur Hälfte zusammengedrückt ist?
12. Der Wagen (m = 20 kg) wird aus dem Stand losgelassen. Die Feder (D = 500 N/m) ist in der Ausgangsposition
um 0,4 m zusammengedrückt.
(a) Wie groß ist die kinetische Energie des Wagens an der Stelle P?
(b) Wie groß ist seine Geschwindigkeit bei P?
(c) Welche maximale Höhe erreicht der Wagen?
(d) Welche Geschwindigkeit hat er, wenn er sich auf der halben maximalen Höhe befindet?
13. Der Wagen wird aus dem Stand losgelassen. Er rollt die schräge Bahn hinunter, stößt gegen die Feder und
wird wieder nach links beschleunigt. Die Reibung ist vernachlässigbar.
(a) Wie groß ist seine kinetische Energie, wenn er zum erstenmal bei P vorbeikommt?
(b) Wie groß ist seine Geschwindigkeit bei P?
(c) Wie groß sind kinetische Energie und Geschwindigkeit, wenn er zum zweiten Mal bei P vorbeikommt?
(d) Um wieviel wird die Feder zusammengedrückt?
(e) Welche Höhe erreicht der Wagen, wenn er wieder zurückkommt?
14. Der Körper wird losgelassen, wenn er sich an der Stelle s = 0,5 m befindet. (Die Feder ist bei s = 0 m
entspannt.)
(a) In welche Richtung setzt sich der Körper in Bewegung? Was für eine Bewegung führt er aus?
(b) An welcher Stelle ist der Nettoimpulsstrom (aus dem Schwerefeld und aus der Feder) gleich 0 N?
(c) Wie groß sind in dieser Höhe die Energie der Feder und die kinetische Energie des Körpers?
15. Stimmt es, dass sich der Bremsweg eines Autos verdoppelt, wenn sich die Geschwindigkeit auf das Doppelte
vergrößert?
(a) Berechne den Bremsweg eines Autos (m = 1000 kg) bei den Geschwindigkeiten 36 km/h und 72 km/h. Der
maximale Impulsstrom, der beim Bremsen aus dem Auto in die Erde fließt, beträgt 4000 N.
(b) Berechne die jeweilige Bremszeit .
16. Eine senkrecht angeordnete Feder mit der Federkonstante D = 30 N/m wird um 20 cm zusammengedrückt.
(a) Wie viel Energie ist in der Feder gespeichert?
(b) Eine 50 g schwere Murmel wird auf die Feder gesetzt und die Feder wird losgelassen. Welche Geschwindigkeit
hat die Murmel 50 cm über ihrer Startposition?
(c) Wie lange dauert es jetzt noch, bis die Kugel den höchsten Punkt ihrer Flugbahn erreicht?
17. Ein 200 g schwerer Stein wird nach oben geworfen. Nach zwei Sekunden trifft er auf die Erde.
(a) Wie groß war seine Anfangsgeschwindigkeit?
(b) Wie groß war seine kinetische Energie am Anfang?
(c) Welche Höhe erreicht er?