Weitere diskrete Wahrscheinlichkeitsverteilungen

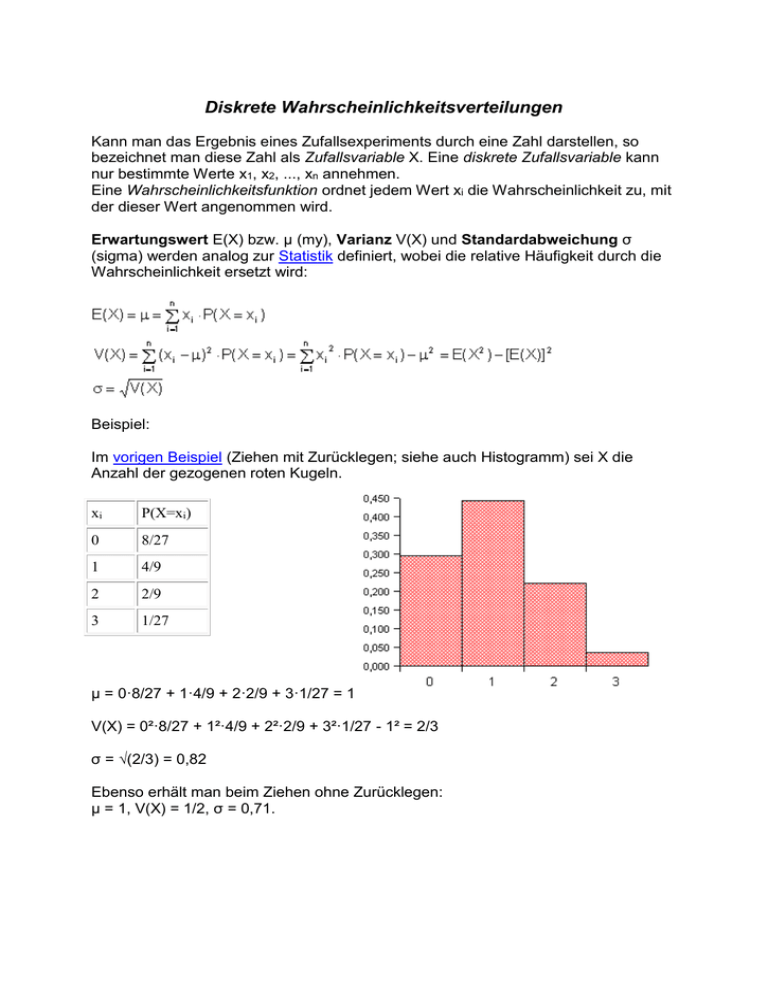
Diskrete Wahrscheinlichkeitsverteilungen
Kann man das Ergebnis eines Zufallsexperiments durch eine Zahl darstellen, so
bezeichnet man diese Zahl als Zufallsvariable X. Eine diskrete Zufallsvariable kann
nur bestimmte Werte x1, x2, ..., xn annehmen.
Eine Wahrscheinlichkeitsfunktion ordnet jedem Wert xi die Wahrscheinlichkeit zu, mit
der dieser Wert angenommen wird.
Erwartungswert E(X) bzw. μ (my), Varianz V(X) und Standardabweichung σ
(sigma) werden analog zur Statistik definiert, wobei die relative Häufigkeit durch die
Wahrscheinlichkeit ersetzt wird:
Beispiel:
Im vorigen Beispiel (Ziehen mit Zurücklegen; siehe auch Histogramm) sei X die
Anzahl der gezogenen roten Kugeln.
xi
P(X=xi)
0
8/27
1
4/9
2
2/9
3
1/27
μ = 0·8/27 + 1·4/9 + 2·2/9 + 3·1/27 = 1
V(X) = 0²·8/27 + 1²·4/9 + 2²·2/9 + 3²·1/27 - 1² = 2/3
σ = √(2/3) = 0,82
Ebenso erhält man beim Ziehen ohne Zurücklegen:
μ = 1, V(X) = 1/2, σ = 0,71.
Die Binomialverteilung
Eine wichtige Wahrscheinlichkeitsverteilung ist die Binomialverteilung. Sie tritt unter
folgenden Bedingungen auf:



Ein Experiment hat nur zwei mögliche Ausgänge A und A'. Dabei sei P(A) = p
und P(A') = q = 1 - p.
Es kann beliebig oft wiederholt werden.
Die Wahrscheinlichkeit von A bzw. A' bleibt bei jeder Wiederholung gleich.
(Ein solches Experiment nennt man Bernoulli-Experiment.)
Dann ist die Wahrscheinlichkeit, dass bei n Wiederholungen k-mal das Ereignis A
eintritt,
(k = 0, 1, 2, ... n)
(n über k) ist der Binomialkoeffizient.
Für Erwartungswert und Standardabweichung ergeben sich die Formeln
Beispiel:
Wir würfeln 12mal mit einem normalen Würfel, X sei die Anzahl der geworfenen
Sechser.
n = 12, p = 1/6, q = 5/6
Die beiden Abbildungen zeigen die Binomialverteilung für p = 1/2 und n = 4 bzw. 16.
Wie man sieht, nähert sich die Form bei wachsendem n immer mehr einer
"Glockenkurve", der Normalverteilung (s. stetige Verteilungen).
Weitere diskrete Wahrscheinlichkeitsverteilungen
Gleichverteilung
Dabei handelt es sich um die einfachste diskrete Verteilung: Jeder ganzzahlige Wert
von 1 bis n wird mit derselben
Wahrscheinlichkeit angenommen.
k = 1, 2, ... n
Beispiel: X ist die Augenzahl bei einmaligem Würfeln mit einem fairen Würfel.
Hypergeometrische Verteilung
Beim Ziehen ohne Zurücklegen können wir nicht mit Binomialverteilung rechnen, weil
sich die Wahrscheinlichkeiten bei jedem Zug ändern. Hier müssen wir auf die Formel
"Anzahl der günstigen Fälle/Anzahl der möglichen Fälle" zurückgreifen.
Wir gehen aus von einer Grundgesamtheit aus N Elementen, von denen K eine
bestimmte Eigenschaft haben. Es werden n Elemente ohne Zurücklegen gezogen. X
sei die Anzahl der Elemente der Stichprobe, die die untersuchte Eigenschaft haben.
Dann gilt:
k = 0, 1, 2, ...
n
(Die Abbildung zeigt das Histogramm einer hypergeometrischen Verteilung mit N =
10, K = 5 und n = 4. Vergleiche mit der entsprechenden Binomialverteilung!)
Beispiel:
Wie groß ist die Wahrscheinlichkeit, beim Lotto "6 aus 45" 4 Richtige zu tippen?
Es gibt (6 über 4) Möglichkeiten, aus den 6 richtigen Zahlen 4 auszuwählen, und (39
über 2) Möglichkeiten, von den 39 falschen Zahlen 2 anzukreuzen. Insgesamt sind
(45 über 6) verschiedene Tipps möglich. Wir erhalten daher für die gesuchte
Wahrscheinlichkeit:
= 0,001365
Poisson-Verteilung
Die Poisson-Verteilung gilt für seltene Ereignisse, die voneinander unabhängig sind.
Man erhält sie als Grenzfall der Binomialverteilung, wenn n sehr groß und p sehr
klein wird. X ist die Anzahl der Ereignisse pro Zeiteinheit. Mit λ = n·p erhält man die
Wahrscheinlichkeit
k = 0, 1, 2, ...
Beachte, dass k beliebig große Werte
annehmen kann. Für große k wird
aber die Wahrscheinlichkeit
verschwindend klein.
Auch die hypergeometrische Verteilung kann man für große n durch die PoissonVerteilung annähern.
Beispiel:
In eine Bibliothek kommen durchschnittlich 3 Benutzer pro Stunde.
Wie groß ist die Wahrscheinlichkeit, dass in der nächsten Stunde 5 Benutzer
kommen?
Wir können die Angabe etwa so auffassen, dass in einer Woche (40 Stunden) 120
Benutzer kommen. Die Wahrscheinlichkeit, dass ein bestimmter Benutzer in der
nächsten Stunde kommt, beträgt 1/40. Daher ist λ = 120/40 = 3. Es handelt sich hier
um einen sogenannten Poisson-Prozess der Dichte 3. Wir erhalten für die gesuchte
Wahrscheinlichkeit
Geometrische Verteilung
Wir betrachten wieder ein Bernoulli-Experiment mit den Wahrscheinlichkeiten P(A) =
p, P(A') = q = 1 - p. Diesmal interessiert uns aber, wie lange wir warten müssen, bis
das Ereignis A zum ersten Mal auftritt. Das ist beim k-ten Versuch der Fall, wenn auf
(k-1) Misserfolge ein Erfolg folgt; die Wahrscheinlichkeit dafür beträgt
P(X=k) = p·qk-1
Auch hier kann k beliebig große Werte
annehmen.
Beispiel: Beim Spiel "Mensch ärgere
dich nicht" darf man eine Figur erst ins
Spiel bringen, wenn man eine Sechs
gewürfelt hat. Wie groß ist die Wahrscheinlichkeit, dass man darauf bis zur dritten
Runde warten muss?
Es ist p = 1/6, q = 5/6. Die gesuchte Wahrscheinlichkeit beträgt daher
P(X=3) = 1/6·(5/6)2 = 0,1157