Einführung in das Thema "Wahrscheinlichkeit"

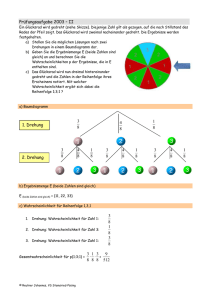
Einführung in das Thema „Wahrscheinlichkeit“
Aufgabe:
a) Drehe das 6-Felder-Glücksrad genau 6-mal.
Wie viel Mal bleibt das Glücksrad wahrscheinlich auf dem Feld mit der Zahl 1 stehen?
Begründe deine Antwort.
Begriffseinführungen:

P (Ereignis)
bedeutet: „Die Wahrscheinlichkeit eines Ereignisses“
Info: P ist die Abkürzung für probability = Wahrscheinlichkeit
Bsp: Glücksrad
P (1)
bedeutet: „Die Wahrscheinlichkeit, dass das Ereignis 1 gedreht wird“
P (2)
bedeutet: „Die Wahrscheinlichkeit, dass das Ereignis 2 gedreht wird“
P (3)
bedeutet: „Die Wahrscheinlichkeit, dass das Ereignis 3 gedreht wird“
P (4)
bedeutet: „Die Wahrscheinlichkeit, dass das Ereignis 4 gedreht wird“

„Anzahl der günstigen Ergebnisse“
Bsp: Glücksrad
Die Zahl 1 kommt auf dem Glücksrad in drei Feldern vor. Auch die Zahl 2 kommt auf einem
Feld vor. Auch die Zahl 3 kommt auf einem Feld vor. Auch die Zahl 4 kommt auf einem Feld
vor.
Man sagt auch:
Die Anzahl der günstigen Ergebnisse für Das Ereignis „1“ ist 3.
Die Anzahl der günstigen Ergebnisse für das Ereignis „2“ ist 1.
Die Anzahl der günstigen Ergebnisse für das Ereignis „3“ ist 1.
Die Anzahl der günstigen Ergebnisse für das Ereignis „4“ ist 1.

„Anzahl aller möglichen Ergebnisse“
Dieses Glücksrad hat sechs mögliche Felder, auf die es gedreht werden kann.
→ Es gibt also hier sechs mögliche Ergebnisse!
Formel zur Berechnung von Wahrscheinlichkeiten:
P (Ereignis) =
𝑨𝒏𝒛𝒂𝒉𝒍 𝒅𝒆𝒓 𝒈ü𝒏𝒔𝒕𝒊𝒈𝒆𝒏 𝑬𝒓𝒈𝒆𝒃𝒏𝒊𝒔𝒔𝒆
𝑨𝒏𝒛𝒂𝒉𝒍 𝒅𝒆𝒓 𝒎ö𝒈𝒍𝒊𝒄𝒉𝒆𝒏 𝑬𝒓𝒈𝒆𝒃𝒏𝒊𝒔𝒔𝒆
Beispiel 1:
Wie hoch ist die Wahrscheinlichkeit, dass das Glücksrad auf das Feld mit der Zahl 1 gedreht
wird?
P (1) =
𝑨𝒏𝒛𝒂𝒉𝒍 𝒅𝒆𝒓 𝒈ü𝒏𝒔𝒕𝒊𝒈𝒆𝒏 𝑬𝒓𝒈𝒆𝒃𝒏𝒊𝒔𝒔𝒆
𝑨𝒏𝒛𝒂𝒉𝒍 𝒅𝒆𝒓 𝒎ö𝒈𝒍𝒊𝒄𝒉𝒆𝒏 𝑬𝒓𝒈𝒆𝒃𝒏𝒊𝒔𝒔𝒆
𝟑
= = O,5 = 50 %
𝟔
Antwort:
Die Wahrscheinlichkeit, dass auf das Feld mit der Zahl 1 gedreht wird, ist 3 zu 6.
Die Wahrscheinlichkeit, dass auf das Feld mit der Zahl 1 gedreht wird, , liegt bei 50 %.
Beispiel 2:
Wie hoch ist die Wahrscheinlichkeit, dass das Glücksrad auf das Feld mit der Zahl 2 gedreht
P (2) =
𝑨𝒏𝒛𝒂𝒉𝒍 𝒅𝒆𝒓 𝒈ü𝒏𝒔𝒕𝒊𝒈𝒆𝒏 𝑬𝒓𝒈𝒆𝒃𝒏𝒊𝒔𝒔𝒆
𝑨𝒏𝒛𝒂𝒉𝒍 𝒅𝒆𝒓 𝒎ö𝒈𝒍𝒊𝒄𝒉𝒆𝒏 𝑬𝒓𝒈𝒆𝒃𝒏𝒊𝒔𝒔𝒆
𝟏
= = O,166 = 16,6 %
𝟔
Antwort:
Die Wahrscheinlichkeit, dass auf das Feld mit der Zahl 2 gedreht wird, ist1 zu 6.
Die Wahrscheinlichkeit, dass auf das Feld mit der Zahl 2 gedreht wird,
liegt bei 16,6 %.