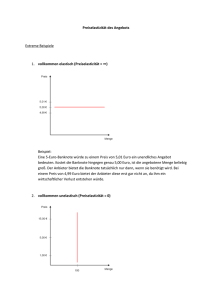
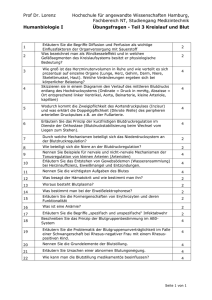
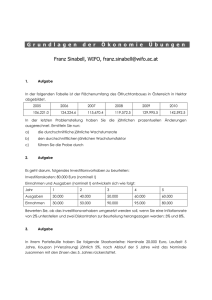
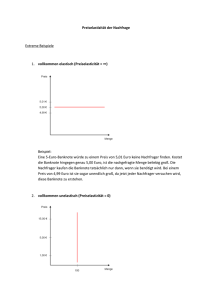
Frage I 1 (10 Punkte)

Dr. M. Ruiz
Fragen der Mikro-Teilklausur HWI SS07 vom 13. Juli 2007
Seite 1 von 3
**************************************************************************************
Dr. M. Ruiz
13. Juli 2007
Mikro-Teilklausur für HWI
Name:
Semesterzahl:______
Vorname:
Matr.Nr.:
Platznr.:______
Wenn das Ergebnis nicht Netz erscheinen soll, bitte hier ankreuzen: _____
Beachten Sie bitte folgendes:
Die Klausur besteht aus 6 Aufgaben, 4 Aufgaben mit je 10 Punkten und 2 Aufgaben
mit je 20 Punkten. Bitte überprüfen Sie die Vollständigkeit Ihres Exemplars.
Bei der Klausur werden nur Lösungen auf den verteilten Blättern berücksichtigt.
Bitte melden Sie sich beim Verlassen des Raumes während der Klausur bei der Aufsicht. Geben Sie Ihre Unterlagen dort ab.
Ergebnisse ohne Ansatz, Begründung bzw. Berechnung , Zeichnungen ohne vollständige Beschriftung werden nicht als vollständige Lösung gewertet.
Als einzige Hilfsmittel sind einfache Taschenrechner und Lineal zugelassen.
Teilklausur Mikroökonomie
Aufgabe:
1
2
3
4
5
6
insgesamt
Bearb.Zeit
Erreichte
Punktzahl
10 min
10 min
10 min
10 min
20 min
20 min
80 min
Insgesamt erreichte Punkte:
Note:
Seite
1
Dr. M. Ruiz
Fragen der Mikro-Teilklausur HWI SS07 vom 13. Juli 2007
Seite 2 von 3
Frage 1 (10 Min)
a) Beschreiben Sie algebraisch und verbal das Konzept der Preiselastizität der Nachfrage. Erläutern Sie das Verhalten eines HH mit einer Preiselastizität von -2.
b) Die Nachfragefunktion eines HH nach einem Gut sei durch p = 12 - 2xN gegeben
(p Marktpreis , xN nachgefragte Menge). Zeichnen Sie die Funktion und bestimmen
Sie den Prohibitivpreis und die Sättigungsmenge. Bestimmen Sie den Preis und die
Menge, bei der die Nachfrageelastizität gleich -2 ist.
c) Die obige Nachfragefunktion trifft auf einem Markt mit einer linearen Angebotsfunktion p = a + bxA mit unbekannten Parametern a und b zusammen. Das Marktgleichgewicht sei bei x* = 2 erreicht. Die Preiselastizität des Angebots sei im Punkt
des Marktgleichgewichts gleich +2. Ermitteln Sie die Parameter a und b.
Frage 2 (10 Min)
a) Zeigen Sie, wie sich die sog. Marshall-Kurve (Preis-Nachfrage-Kurve) für Gut 2
aus einer Folge von Haushaltsgleichgewichten (Preis-Konsum-Kurve im x1-x2Diagramm) grafisch herleiten läßt. (Vollständige Bezeichnung aller Kurven und relevanten Punkte)
b) Die Grenzrate der Substitution von Orangensaft zu Apfelsaft sei bei einem bestimmten HWI-Studenten ungewöhnlicherweise immer gleich 1, egal, wieviel Apfelsaft er konsumiert. Wie sehen seine Indifferenzkurven aus?
c) Konstruieren Sie bei gegebenem Preis für O-Saft von pO = 2 und gegebener Konsumsumme von e= 10 die Haushaltsgleichgewichte für verschiedene denkbare Preise des Apfelsafts und leiten Sie daraus die Marshall-Kurve für Apfelsaft her. Wie
groß ist die Preiselastizität der Apfelsaftnachfrage?
Frage 3 (10 Min)
a) Zeigen Sie, wie sich der Gesamteffekt einer Preissenkung bei Gut 1 nach Hicks in
einen Substitutionseffekt und einen Einkommenseffekt zerlegen läßt.
(Grafische Analyse in einem (x1,x2)-Diagramm mit ausführlicher Beschriftung, Erklärung der verwendeten Budgetgeraden und Kommentar)
b) Erläutern Sie die denkbaren Wirkungsrichtungen des Substitutionseffekts und des
Einkommenseffekts aufgrund der hier unterstellten Preissenkung bei Gut 1 auf die
Nachfrage nach Gut 1.
c) Erklären Sie, was man unter dem Spezialfall eines Giffen-Gutes versteht.
Woran kann man bei der Analyse des Substitutionseffektes und des Einkommenseffektes einer Preissenkung bei Gut 1 erkennen, ob es sich bei dem untersuchten Gut
1 um ein Giffen-Gut handelt? (neue Grafik mit deutlich erkennbaren Effekten und mit
Kommentar). Wie verläuft die Engel-Kurve und wie die Marshall-Kurve eines GiffenGutes?
Frage 4 (10 Min)
a) Gegeben seien die Preise p1 und p2 sowie das Einkommen e. Leiten Sie für eine
Nutzenfunktion vom Cobb-Douglas-Typ U = x1a. x2b mit den festen Koeffizienten
a,b>0 nach Lagrange das Haushaltsoptimum her und bestimmen Sie daraus die beiden Güternachfragefunktionen des HH für x1 und für x2..
b) Erläutern Sie die nach diesen Funktionen sich ergebenden Auswirkungen einer
Änderung von e auf x1 und von e auf x2. Wie groß sind die Einkommenselastizitäten
von Gut1 und von Gut2?
c) Erläutern Sie die Auswirkungen einer Änderung von p1 auf x1 und einer Änderung
von p2 auf x2. Wie groß sind die Preiselastizitäten von Gut1 und von Gut2?
Wie groß ist hier der Einfluß von p2 auf x1 und von p1 auf x2? Wie groß sind die
Kreuzpreiselastizitäten von Gut1 und von Gut2?
Seite
2
Dr. M. Ruiz
Fragen der Mikro-Teilklausur HWI SS07 vom 13. Juli 2007
Seite 3 von 3
Frage 5 (20 Minuten)
Zwei Unternehmen A und B konkurrieren um die Nachfrage auf auf einem Markt. Sie
verfügen über jeweils drei Strategien S1, S2 und S3 , über die sie vorab ohne Absprachen entscheiden müssen.
A
S1
Auszahlungsmatrix
B
S1
S2
S3
2/9
1/5
5/8
S2
3/2
2/3
1/2
S3
4/2
1/4
3/5
a) Was versteht man unter einer dominanten Strategie? (Definition)
b) Untersuchen Sie, ob A oder/und B über eine dominante Strategie verfügt und wo
sie ggf. liegt. (mit ausführlicher Untersuchung und Begründung)
c) Was versteht man unter einem Nash-Gleichgewicht? (Definition)
d) Prüfen Sie, ob es stabile Gleichgewichte (Nash-Gleichgewichte) gibt und wo es/sie
ggf. liegen. (Erläuterung des Lösungsweges und ausführliche Untersuchung jeder
einzelnen Strategiekombination)
e) Was versteht man unter einem "Gefangenendilemma"? (Defininiton) Untersuchen
Sie, ob hier solche Dilemma-Situationen vorliegen.
Frage 6 (20 Minuten)
Die Präferenzordnung eines typischen HH sei beschrieben durch die Nutzenfunktion
U = x12x2 . Die Güterpreise seien p1 = 4 und p2 = 2
a) Berechnen Sie die nutzenmaximalen Verbrauchsmengen für eine Konsumsumme
von 600 Euro.
b) Bestimmen Sie die Opportunitätskosten des Konsums einer zusätzlichen Einheit
von Gut 2.
c) Bestimmen Sie die Grenzrate der Substitution von Gut 1 durch Gut 1 im Haushaltsoptimum.
Wie verändert sich die Güternachfrage im HH-Optimum,
d) - wenn sich der Preis für Gut 2 verdoppelt?
e) - wenn der Staat für Gut 1 eine Preissubvention von Euro 2,- je Mengeneinheit
einführt?
f) - wenn der Staat den HH eine pauschale Summe (Einkommenssubvention)
zukommen läßt, die genau so gross ist wie der Subventionsbetrag unter (e).
g) Vergleichen Sie für den HH den Nutzen der Preissubvention unter (e) mit dem
Nutzen der Einkommenssubvention unter (f). (Berechnung)
h) Erläutern sie allgemein mit einer grafischen Analyse, warum ein beliebiger HH in
aller Regel eine pauschale Subvention einer Preissubvention (bei gleichen Subventions-Kosten für den Staat) vorziehen wird. Mit welcher Begründung werden trotzdem
häufig Preise subventioniert?
Seite
3