1.4 Kinetik des starren Körpers

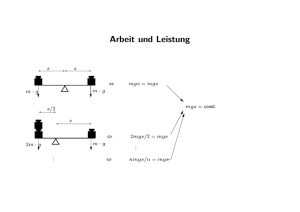
1.4
Kinetik des starren Körpers
In diesem Kapitel rücken wieder Kräfte und Momente als Ursache der Bewegung in unseren Fokus. Nach den Überlegungen zur Kinematik der starren Scheibe müssen wir über
die Änderung des translatorischen Bewegungszustand eines geeigneten Referenzpunktes,
vormals mit A bezeichnet, und über die Änderung der Rotation des starren Körpers um
diesen Referenzpunkt Aussagen machen können. Beides kann wie wir sehen werden getrennt abgehandelt werden. In einem ersten Unterkapitel werden wir die translatorischen
Bewegung abhandeln, in einem zweiten Unterkapitel schließlich die Rotation.
z
1.4.1
Schwerpunktsatz
F
M
Ein Körper kann im algemeinen Fall durch Kräfte und Momente
belastet werden. Die Abbildung zeigt die resultierende Kraft F⃗
⃗ . Die Newtonsche Bewegungsund das resultierende Moment M
gleichung hatten wir bisher für Massenpunkte allenfalls für Systeme von Massenpunkten kennen gelernt. Es liegt nun nahe den
Körper in differentielle Massenelemente aufzuteilen, die wir wie
Massenpunkte behandeln wollen. Die Newtonsche Bewegungsgleichung für eine freigeschnittenes Massenelement dm liefert
m
y
x
dm
dMdm
dFdm
vdm
wobei die resultierende Kraft dF⃗dm auf den Massenpunkt äußere und innere Kräfte beinhaltet18) . Außerdem können alle Massenelemente verschiedene Geschwindigkeiten ⃗vdm aufweisen,
was durch den Index an der Geschwindigkeit vermerkt wird. Um den gesamten Körper zu erfassen, integrieren wir über alle Massenelemente
Wenn wir stets die gesamte Masse des Körpers im Auge halten, so ist m = const und die Zeitdifferentiation kann vor das Integral links vom Gleichheitszeichen gezogen werden. Das Inegral
auf der rechten Seite liefert uns die resultierende äußere Kraft F⃗ auf den Körper:
z
Die zeitliche Differentiation der Bestimmungsgleichung für den Ort
des Schwerpunkts
F
vS
M
aS S
m
liefert für die Schwerpunktsgeschwindigkeit ⃗vS
x
y
so dass wir endgültig
18)
Die Momente tauchen in dieser Gleichung nicht auf, da sie als Kräftepaare darstellbar sind und damit keinen Beitrag zur resultierenden Kraft liefern. Die freien Momente und die Momente der Kräfte werden bei der
Berechnung der Rotation des Körpers Eingang finden.
82
erhalten.
Das Ergebnis ist sehr einfach zu interpretieren. Der Schwerpunkt eines ausgedehnten Körpers
der Masse m wird unter dem Einfluss der äußeren Kräfte so beschleunigt, als ob die Masse des
Körpers im Schwerpunkt konzentriert ist.
Schwerpunktsbeschleunigung ⃗aS und resultierende Kraft F⃗ sind zueinander parallel, ihre Wirkungslinien müssen jedoch nicht zusammenfallen19) .
Es sei ausdrücklich darauf hingewiesen, dass wir bei dieser Herleitung die Näherung des starren
Körpers nicht genutzt haben. Genau die gleiche Aussage hatten wir auch bereits für ein System
von Massenpunkten im Abschnitt über den Impulssatz und bei der Behandlung von Streu und
Stoßproblemen erhalten.
Das Ergebnis rechtfertigt im Nachhinein die Kinetik des Massenpunktes als eine sehr brauchbare
Approximation der Wirklichkeit für solche Probleme, bei denen die binnenkörperliche Rotation
keine wichtige Rolle spielt.
Die Beschreibung der Rotation des Körpers wollen wir an dieser Stelle noch zurückstellen und
zunächst die mathematische Beschreibung mechanischer Energieformen für den starren Körper
nämlich die potentielle Energie und die kinetische Energie vornehmen.
19)
Es sei explizit darauf hingewiesen, dass die Lage der Wirkungslinie hinsichtlich der Rotationsbewegung des
Körpers, die durch Winkelgeschwindigkeit φ
⃗˙ und Winkelbeschleunigung φ
⃗¨ beschrieben wird, eine Rolle spielt.
Die Momente der Kräfte und auch freie Momente bewirken eine zeitliche Änderung des Drehimpulses. Für die
Beschleunigung aller anderen Punkte A des Körpers, die nicht mit dem Schwerpunktes S zusammenfallen, können
wir für den starren Körper mit der Eulerschen Formel die Beschleunigung
(
)
⃗aA = ⃗aS + ⃗aA,S = ⃗aS + φ
⃗˙ × φ
⃗˙ × ⃗rA,S + φ
⃗¨ × ⃗rA,S .
berechnen.
83
1.4.2
Potentielle und kinetische Energie des Körpers
Potentielle Energie in konstantem Schwerefeld
Wir hatten beim Massenpunkt die potentielle Energie als die negative Arbeit der Gewichtskraft
bei der Verschiebung im Schwerefeld eingeführt. Wir teilen den Körper in infinitesimale Massenelemente dm auf und übernehmen diese Definition für jedes Massenelement:
z
g
G
Wir erleichtern uns die Herleitung, indem wir einen starren Körper
annehmen. Dann können wir die Verschiebung d⃗rdm mit Euler
durch
dm S m
A
x
⃗ = ⃗g dm in die obige Beausdrücken und dies zusammen mit dG
ziehung einsetzen:
y
dG
dm
dFdm
dMdm drdm
Integrieren für alle Massenelemente des Körpers
Die beiden Integrale können dabei sofort vereinfacht werden, da ⃗g und wegen des starren Körpers
auch d⃗rA und d⃗
φ für alle Massenelemente den gleichen Wert haben:
Es bietet sich hier nun an, den Punkt A geschickt zu wählen. Identifizieren wir nämlich A mit
dem Schwerpunkt des starren Körpers S, so verschwindet
Es ergibt sich für die potentielle Energie
Die potentielle Energie des starren Körpers berechnet sich also aus der Verschiebung des Schwerpunkts des starren Körpers im Schwerefeld, genau so, als ob die Gesamtmasse im Schwerpunkt
konzentriert ist. Diese Aussage ist auch unabhängig davon, ob der Körper bei der Verschiebung
rotiert oder nicht.
84
Orientieren wir die Schwerebeschleunigung antiparallel zur z-Achse so wird ⃗g = (0, 0, −g)
und für eine endliche Verschiebung vom Ort 1 zum Ort 2
Übung Zeigen Sie, dass sich auch ein deformierbarer Körper hinsichtlich der potentiellen Energie
wie ein Massenpunkt verhält, das heißt, dass alleine die Lage des Schwerpunkts im Schwerefeld
die Potentielle Energie bestimmt!
Kinetische Energie des starren Körpers
z
Auch für die Bestimmung der kinetischen Energie eines ausgedehnten Körpers wollen wir wieder vom Massenpunkt ausgehen. Die kinetische Energie eines infinitesimalen Massenpunktes ist demnach
und für den Körper insgesamt
vdm
dm S m
A
x
y
Die Geschwindigkeit jedes Massenelementes des starren Körpers kann unterschiedlich sein. Wir
vermuten, dass wieder der Schwerpunkt S eine besondere Rolle spielt und wir könnten ⃗vdm mit
Euler durch
ausdrücken. Oft rotiert aber ein betrachteter Körper um einen festen Punkt, durch den die Achse
der Drehbewegung verläuft. Wir wollen deshalb allgemeiner formulieren und einen zunächst
unbestimmten Punkt A als Referenzpunkt wählen:
In der Definition für die kinetische Energie benötigen wir das Quadrat der Geschwindigkeit
Wir multiplizieren dies aus und erhalten
so das unter Formel für die kinetische Energie
lautet.
85
Das erste Integral liefert, wenn wir berücksichtigen, dass die Geschwindigkeit ⃗vA des Referenzpunktes A als translatorischer Beitrag für alle Massenelemente konstant ist,
Im zweiten Integral setzen wir außerdem ⃗vdm,A = φ
⃗˙ × ⃗rdm,A und berücksichtigen, dass für den
starren Körper φ
⃗˙ = const, so dass sich
ergibt. Im dritten Integral schließlich müssen wir
auswerten. Wir nutzen hierfür die Lagrangesche Identität20)
so dass
Der Ausdruck
ist eine rein geometrische Größe, der nur von der Massenverteilung im Körper abhängt. JA wird
Massenträgheitsmoment bezogen auf den Punkt A genannt. Das Massenträgheitsmoment bezogen auf eine Punkt wird umso größer, je weiter Teile der Gesamtmasse eines Körpers vom Punkt
A entfernt sind, hohle Körper haben daher ein größere Massenträgheitsmoment als kompakte
Körper21) . Die weitere Diskussion und die Berechnung von Massenträgheitsmomenten wollen
wir an dieser Stelle noch zurückstellen.
20)
Die Umrechnung mit der Lagrangeschen Identität ist eine Möglichkeit der Darstellung der kinetischen Energie
abzuleiten, die insbesondere dann praktisch ist, falls vorrangig ebene starre Körper betrachtet werden sollen. Die
Darstellung der kinetischen Energie durch den Trägheitstensor soll hier nicht genutzt werden.
21)
Die Formel für das Massenträgheitsmoment erinnert an die Definition des Flächenträgheitsmomentes I in
der Festigkeitslehre. Ein großes Flächenträgheitsmoment hatten wir bei Balken als Ursache für einen großen
Widerstand gegen Verbiegung identifiziert. Die bei einer Verformung gespeicherte Energie wächst mit wachsendem Flächenträgheitsmoment. Entsprechend zeigt ein großes Massenträgheitsmoment in der Kinetik an, dass ein
Körper großen Trägheitsmomentes eine große Rotationsenergie speichert, beziehungsweise eine große Trägheit
gegen Änderung des Rotationszustands aufweist.
86
Wir erhalten zusammengefasst folgenden Ausdruck für die kinetische Energie des starren Körpers
Insbesondere der letzte Term zeigt einen komplizierten Beitrag zur kinetischen Energie, in den
die Richtungsabhängigkeit zwischen momentaner Drehachse in Richtung φ
⃗˙ /φ̇ und Lage der
Massenteilchen des Körpers eingeht.
Einfachere Formeln erhalten wir, falls wir den Referenzpunkt A mit dem Schwerpunkt S identifizieren, dann ist stets ⃗rS,A = ⃗0 sowie ⃗va = ⃗vS und es tritt das Massenträgheitsmoment bezüglich
des Schwerpunkts
auf. Es ergibt sich
Der letzte Term verschwindet erst, wenn alle Massenteilchen eines Körpers senkrecht zur momentanen Drehachse in Richtung φ
⃗˙ /φ̇ angeordnet sind. Dies ist der Fall falls es sich um einen
ebenen starren Körper handelt, dessen Drehachse senkrecht zur Ausdehnung des Körpers orientiert ist.
Für die kinetische Energie eines ebenen starren Körpers erhalten wir die einfache Beziehung
Der erste Anteil stellt den Anteil der Translation des Körpers dar. Da alle Massenelemente die
gleiche Translation ausführen ist dieser Anteil nicht zu unterscheiden von der kinetischen Energie
eines Massenpunktes gleicher Masse und Geschwindigkeit. Bei ausgedehnten Körpern ist aber
zusätzlich Energie
in der Rotation gespeichert, die beim Massenpunkt keine Rolle spielen kann,
∫
da
lim
rdm,S →0
(m)
2
rdm,S
dm = 0.
Wir können die kinetische Energie des ebenen starren Körpers aufteilen in einen translatorischen
und eine rotatorischen Anteil
Wir erkennen einen analogen Aufbau der Formel für die beiden Energieanteile, der einen Gedächtnishilfe darstellt.
Es sei explizit darauf hingewiesen: Eine ähnlich einfache Aufteilung der kinetischen Energie ist
für keinen anderen Punkt A ̸= S im Körper möglich,
auch nicht für den ebenen Körper, da zwar nach wie vor
gilt, jedoch der Term
87
in unserer vollständigen Formel im Allgemeinen nicht verschwindet.
Dieser wird nur dann sicher Null, falls der Bezugspunkt A überhaupt keine Geschwindigkeit
besitzt. Ein Fall der oft auftritt. Denn der Punkt A muss lediglich auf der Drehachse angesiedelt
sein und in dem Koordinatensystem, aus dem die Geschwindigkeiten heraus definiert sind, ruhen:
Dieser Fall tritt bei technischen Anwendungen außerordentlich oft auf. Unter dieser Bedingung
gilt für den ebenen Körper bei Rotation um einen im Bezugssystem ruhenden Achspunkt A:
In diesem Ausdruck tritt dann kein translatorischer Energiebeitrag auf.
Übung
m
Zeigen Sie, dass für die kinetische Energie des dargestellten ebenen
starren Körpers
gilt.22)
S
ϕ
Teben
1
1
1
= m vS2 + JS φ̇2 ≡ JA φ̇2
2
2
2
mit
JA = JS + m rS2
22)
y
A
x
Der Anteil m rS2 des Massenträgheitsmoment bezüglich des Punktes A wird Steinerscher Anteil genannt.
Offensichtlich ist das Trägheitsmoment eines Körpers bezüglich des Schwerpunkts das kleinste. Bei Drehung um
eine Achse außerhalb des Schwerpunkts erhäht sich das Trägheitsmoment um den stets positiven Steinerschen
Anteil, der sich aus dem Abstandsquadrat und der Gesamtmasse des Körpers errechnet.
88
Beispiel
Ein Rad vom Radius r und homogener Masseverteilung rollt
ohne zu rutschen aus der Ruhelage eine schiefe Ebene hinunter.
Bestimmen Sie in Abhängigkeit von der Strecke s die kinetische
Energie, die Geschwindigkeit des Rades und seine Beschleunigung,
g
s
S
r
a) wenn das Rad als ebener starrer Körper, Index SK, betrachtet wird,
α
b) wenn das Rad zum Vergleich als Massenpunkt, Index M P ,
betrachtet wird!
Lösung
s
S
Wir nutzen den Energiesatz nach dem kinetische und potentielle Energie bei s = 0 zuzüglich der Arbeit der Kräfte entlang
der zurückgelegten Strecke s mit der kinetischen und potentiellen Energie an der Stelle s übereinstimmt:
m, r
α
Dabei ist mit ΣF⃗ die Resultierende aller am Körper angreifenden Kräfte außer der Gewichtskraft
gemeint, die ja bereits durch die potentielle Energie erfasst wird. Dazu ist ein Freischnitt sinnvoll.
Setzen wir kinetische und potentielle Energie bei s = 0 zu Null erhalten wir
⃗ senkrecht zur Bewegungsrichtung steht, verschwindet ihre Arbeit:
Da die Normalkraft N
Das Integral über die Reibkraft verschwindet ebenfalls
Dies sieht man ein, wenn man die Reibkraft in den Mittelpunkt des Rades parallel verschiebt
und das dadurch entstehende Versatzmoment MR in den Freischnitt einträgt. Die Arbeit der
Reibkraft und die Arbeit des Versatzmomentes ergänzen sich genau zu Null. Wir erhalten also
einfach
wobei
Für das rollende Rad auf der feststehenden schiefen Ebene hatten wir vS = r φ̇ gefunden, so
dass wir für die kinetische Energie den Ausdruck
89
erhalten. Für das Massenträgheitsmoment
finden wir mit m(rdm ) = m
2
π rdm
→ dm = m 2 rdm drdm /r2
π r2
und daher
oder
Die Beschleunigung aS (s) des Rades erhalten wir, indem wir die Beziehung für die Geschwindigkeit nach der Zeit t ableiten:
b) Vergleichen wir das Ergebnis für den sich ohne Reibungsverluste auf der Ebene bewegenden
Massenpunkt, so erhalten wir aus dem Energiesatz
Das Verhältnis der kinetischen Energien,der Geschwindigkeiten und der beschleunigungne ist
also
Der reibungsfrei gleitende Massenpunkt nimmt demnach schneller Geschwindigkeit auf als der
starre Körper. Die zur Verfügung stehende potentielle Energie wird beim starren Körper nicht
nur in translatorische kinetische Energie sondern auch in rotatorische kinetische Energie überführt.
In der Summe wird in beiden Fällen die vorhandene potentielle Energie vollständig in kinetische
Energie umgesetzt! Schwerpunktsbeschleunigung und -geschwindigkeit sind beim rollenden Rad
notwendigerweise kleiner als beim Massenpunkt, schließlich bremst die Reibkraft die Schwerpunktsbewegung. Für die Zunahme der Winkelgeschwindigkeit und damit der rotatorischen kinetischen Energie ist die Reibkraft zuständig. Dadurch, dass diese am Umfang angreift, kann
sie die Rotationsgeschwindigkeit des Rades so erhöhen, wie es die Abrollbedingung erfordert.
In Einklang mit unserer Aussage, dass die Reibkraft keine Arbeit leistet, schlägt also durch die
Reibung beim rollenden Rad kein Verlust mechanischer Energien zu Buche23) .
Zur Berechnung der Reibkraft werden wir im folgenden Abschnitt den Drehimpulssatz für den
starren Körper verwenden, dessen Herleitung uns noch fehlt und die Kinetik des starren Körpers
vervollständigt.
23)
Die Reibkraft am rollenden Rad kommt durch Haftreibung zustande. Im Unterschied zur Rollreibung, die
einhergeht mit der Deformation des rollenden Körpers, kann beim starren Körper keine Rollreibung auftreten!
90
Massenträgheitsmomente einfacher Körper
Ebener Körper
y
S
dm
r
x
Mit der Definition
m
ergeben sich folgende Formeln
Kreisscheibe oder Walze
S
r
Kreisring oder Rohr
S
r
s
Rechteck oder Quader
S
b
a
Stab oder Platte
S
d
l
Es gilt der Satz von Steiner:
y
Offensichtlich ist das Massenträgheitsmoment bezüglich des
Schwerpunkts stets das kleinste für einen gegebenen Körper.
rS
S
x
A
Massenträgheitsmoment der homogenen Kugel um eine Symmetrieachse
z
Rotiert eine homogene Kugel um eine Schwerpunktsachse so
ist das Massentägheitsmoment durch
√
S
x2a
ya2
wobei ra =
+
den Abstand der Massenelemente dm
von der Achse darstellt, wenn diese nach der z-Richtung
ausgerichtet ist.
x
m,R
y
Zur Berechnung des Integrals nutzen wir die Symmetrie der Kugel aus und betrachten das
einfachere Integral
91
Es ist nun wegen der Symmetrie
R′3
Da die Masse kubisch mit dem Radius anwächst m(R′ ≤ R) = m 3 , lässt sich die IntegratiR
onsvariable substituieren durch
so dass wir das Ergebnis
erhalten.
Übungen
a) Vergleichen Sie das Massenträgheitsmomentes eines dünnwandigen Rohres der Masse m
mit einem Vollstab der gleichen Masse!
b) Bestimmen Sie das Massenträgheitsmoment eines dickwandigen Rohres der Masse m mit
Innenradius ri und Außenradius ra !
∫
c) In der Festigkeitslehre hatten wir das polare Flächenträgheitsmoment Ip =
r2 dA defi(A)
niert. Zeigen Sie, dass der Zusammenhang
JS =
Ip
m
A
gilt!
d) Beweisen Sie den Satz von Steiner!
e) Bestimmen Sie das Massenträgheitsmoment einer Hohlkugel aus homogenem Material mit
Innenradius ri und Außenradius ra !
92
Beispiel
Ein homogener Quader der Masse m gleitet reibungsfrei in
einer Halfpipe aus der Ruhelage 1 in die Position 2.
g
r
M
1
Geg.: m , a , b , r , ⃗g
b
a
S
2
Ges.: Winkelgeschwindigkeit α
⃗˙ 2 in der Position 2!
Lösung
Da der Quader reibungsfrei gleitet gilt der Energieerhaltungssatz
M
1
b
S
Die kinetische Energie setzt sich zu jedem Zeitpunkt aus der
translatorischen kinetischen Energie des Schwerpunkt und
der Rotationsenergie um den Schwerpunkt zusammen
2
S
a
Der Quader dreht aber auch um den in unserem Bezugssystem raumfesten Mittelpunkt der
Halfpipe, so dass wir auch
schreiben können, wobei ρ den Kreisradius der Bahnkurve des Schwerpunkts S bezeichnet. Der
Schwerpunkt überstreicht auf dem Weg von 1 nach 2 einen Winkel von π/2. Damit errechnet
sich die Abnahme an potentieller Energie:
Mit den geometrischen Beziehungen
folgt
Mit T1 = 0 folgt daher
Kontrollen:
Einheit: [α2 ] =
1 ( kg m/s2 m )1/2 √
=
s
kg m2
Spezialfall Massenpunkt:
Mit a = b = 0 gilt ∆h = r und mit JM = mr2 folgt für die Winkelgeschwindigkeit das bekannte
Ergebnis:
93