PDF_Lösungen

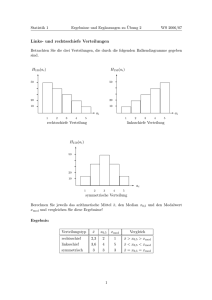
Heinz Holling & Günther Gediga
Statistik - Deskriptive Verfahren
Lösungen zu den Übungen
Version 15.12.2010
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
Inhaltsverzeichnis
1 Lösung zu Übung 1; Kap. 4
3
2 Lösung zu Übung 2; Kap. 5
5
3 Lösung zu Übung 3; Kap. 6
7
4 Lösung zu Übung 4; Kap. 7
9
5 Lösung zu Übung 5; Kap. 7
10
6 Lösung zu Übung 6; Kap. 8
12
7 Lösung zu Übung 7; Kap. 8
13
8 Lösung zu Übung 8; Kap. 8
14
9 Lösung zu Übung 9; Kap. 8
16
10 Lösung zu Übung 10; Kap. 9
17
11 Lösung zu Übung 11 Kap. 10
18
12 Lösung zu Übung 12 Kap. 10
19
2
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
1
Lösung zu Übung 1; Kap. 4
1. Jahreseinkommen:
Die Messung kann über das Brutto- oder Nettogehalt in EURO oder durch Hochrechnen eines Monatsgehalts erfolgen. Es handelt sich hier um eine Messung auf Verhältnisskaleniveau
(absoluter Nullpunkt vorhanden, Abstände interpretierbar).
2. soziale Schicht:
Die Messung kann durch die Einteilung in drei Kategorien (Unter-, Mittel- und Oberschicht,
in der Literatur oft anzutreffen) erfolgen oder auch durch die Erhebung der Ausprägungen verschiedener Merkmale wie Zugehörigkeit zu bestimmten Einkommenskategorien, Schulabschluss,
Wohnsituation. Die Messung erfolgt hier auf dem Niveau einer Ordinalskala (Ausprägungen
können geordnet werden, Abstände nicht interpretierbar).
3. Depressivität:
Zur Messung kann hier ein Fragebogen eingesetzt werden. Dabei gibt die Person beispielsweise
den Grad ihrer Zustimmung (etwa fünf Antwortkategorien von stimme überhaupt nicht zu“ bis
”
stimme voll zu“) zu Aussagen wie Ich habe häufig traurige Gedanken.“, Ich habe Schwierigkei”
”
”
ten aufzustehen.“ oder Ich finde alles uninteressant.“ an. Ordnet man den Antwortmöglichkeiten
”
die Zahlen 1 − 5 (entsprechend stärkerer Zustimmung) zu, so kann man die Zahlenwerte, die den
Antworten entsprechen, über alle Aussagen im Fragebogen summieren. In der Regel geht man
davon aus, dass hiermit eine Messung auf dem Niveau einer Intervallskala möglich ist, weil die
Abstände zwischen den fünf Antwortkategorien als gleich groß angenommen werden.
4. Geschlecht:
Das Geschlecht wird in die Kategorien männlich und weiblich eingeteilt. Es kommt also nur
in zwei Ausprägungen vor. Den Kategorien können beliebige Zahlen (zum Beispiel männlich 0
und weiblich 1) zugeordnet werden. Diese zugeordneten Zahlen müssen eindeutig für nur eine
der beiden Kategorien stehen und sind selbst nicht interpretierbar. Die Messung erfolgt also auf
dem Niveau einer Nominalskala.
5. Temperatur:
Zur Messung wird in der Regel ein Thermometer eingesetzt. Es gibt keinen natürlichen Nullpunkt. Die Temperatur kann beispielsweise in Fahrenheit und in Celsius angegeben werden.
Wasser friert bei 32 ◦ F bzw. 0 ◦ C. Die Aussage, 20 ◦ C seien doppelt so viel wie 10 ◦ C, ist nicht
sinnvoll. Die Messung erfolgt damit auf dem Niveau der Intervallskala und nicht auf dem Niveau einer Verhältniskala. Es ist kein absoluter Nullpunkt vorhanden; Vergleiche von Differenzen
zwischen Temperaturen sind jedoch sinnvoll).
6. Schulnoten:
Bei den Schulnoten können die Kategorien 1 − 6 in eine hierarchische Ordnung gebracht werden.
Das bedeutet für das deutsche Schulsystem, 1 ist die beste Leistung und 6 die schlechteste.
Schulnoten haben also mindestens Ordinalskalenniveau. Strittig ist jedoch, ob die Abstände
zwischen den Noten interpretierbar sind. Der Abstand zwischen den Noten 1 und 2 müsste dann
beispielsweise den gleichen Leistungsunterschied abbilden wie der Abstand zwischen den Noten
4 und 5. Würde man davon ausgehen, dass die Abstände gleich gross sind, könnte die Messung
auch auf dem Niveau einer Intervallskala erfolgen.
7. Bindungstypen:
Die Messung der Bindungstypen erfolgt über die Methode der Beobachtung. Ainsworth und Mitarbeiter entwickelten ein Laborverfahren, mit dem es möglich war, das Verhalten von Kindern,
die von der Mutter getrennt eine Zeit lang mit einer fremden Person alleine gelassen wurden,
systematisch zu beobachten. Anhand des Verhaltens der Kinder, welches beim Weggehen und der
3
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
Rückkehr der Mutter beobachtet wurde, wurde der Bindungstyp bestimmt. Die drei Bindungstypen können als Kategorien aufgefasst werden, denen die Babys eindeutig zugeordnet werden.
Die Kategorien sind nicht geordnet und die Messung erfolgt damit auf Nominalskalenniveau.
4
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
2
Lösung zu Übung 2; Kap. 5
1. Balkendiagramm:
2. Stamm-Blatt Diagramm:
Einheiten: Stamm:10, Blätter:1
8899
000112
9
10
Aufgrund der geringen Datenmenge in dieser Aufgabe sind das Balkendiagramm und das StammBlatt-Diagramm gleich informativ, da die einzelnen Ausprägungen und die Anzahl der Ausprägungen aus beiden Diagrammformen direkt abgelesen werden können. Das Balkendiagramm
hat gegenüber dem Stamm-Blatt-Diagramm in diesem Fall jedoch den Vorteil, dass die Verteilung der IQ-Werte besser abgelesen werden kann.
5
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
3. Empirische Verteilungsfunktion:
6
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
3
Lösung zu Übung 3; Kap. 6
1. Zunächst wirdP
der Mittelwert ȳ der Beobachtungen bestimmt. Die Summe aller Beobachtungen
hat den Wert 11
i=1 yi = 74, woraus sich der Mittelwert ȳ = 74/11 = 6.7273 ergibt.
Pn
1
2
2
Die Varianz wird mit der angegebenen rechentechnisch günstigen Formel s2Y = n−1
i=1 yi − nȳ
unter Verwendung der folgenden Tabelle berechnet:
i
yi
yi2
1
2
3
4
5
6
7
8
9
10
11
P
10
8
5
4
5
10
7
0
9
10
6
100
64
25
16
25
100
49
0
81
100
36
74
596
P
Die Summe ni=1 yi2 = 596 der quadrierten Beobachtungen finden wir in der letzten Zeile und
dritten Spalte der Tabelle. Der Mittelwert von ȳ = 6.7273 wurde bereits berechnet. Beide Werte
werden nun in die oben angegebene Formel eingesetzt. Wir erhalten somit für die Varianz das
Ergebnis
1
1
s2Y = 10
(596 − 11 × 6.72732 ) = 10
(596 − 497.82) = 98.18/10 = 9.82.
√
Die Standardabweichung ist sY = 9.82 = 3.13, d. h. die Wurzel aus der Varianz.
Der Index Y am Symbol s2 für die Varianz bzw. s für die Standardabweichung dient hier nur
dazu, um zu verdeutlichen, dass die ursprüngliche (nicht transformierte) Variable Y betrachtet
wird. Bei der Berechnung des Mittelwertes wurden mehr Nachkommastellen verwendet, damit
das Ergebnis für die Varianz und die Standardabweichung hinreichend genau wird.
2. Jede der ursprünglichen Beobachtungen yi kann in eine Beobachtung yi0 auf der Selbsteinschätzungsskala, welche von 0 bis 100 reicht, umgerechnet werden, indem man die in der Aufgabenstellung
angegebene Formel yi0 = 5yi + 50 verwendet. Bei dieser Formel handelt es sich um eine lineare
Transformation der Form yi0 = byi + a (hier ist b = 5 und a = 50).
Man könnte nun tatsächlich jede einzelne der ursprünglichen Beobachtungen transformieren und
dann erneut den Mittelwert, die Varianz und die Standardabweichung für die transformierte Variable Y 0 auf die gleiche Weise wie in Teilaufgabe 1) ausrechnen. Dies ist aber nicht erforderlich,
da wir wissen, wie sich der Mittelwert, die Varianz und die Standardabweichung bei linearen
Transformationen verändern. Konkret bedeutet das, dass der Mittelwert ȳ 0 der transformierten
Beobachtungen ausgerechnet werden kann, indem man die lineare Transformation auf den Mittelwert ȳ = 6.7273 der nicht transformierten Beobachtungen anwendet. Als Ergebnis erhalten
wir dann
ȳ 0 = 5ȳ + 50 = 5 × 6.7273 + 50 = 83.6365.
Die Varianz s2Y 0 der transformierten Beobachtungen kann aus der Varianz s2Y der ursprünglichen
Beobachtungen berechnet werden, indem man s2Y mit dem Quadrat der Steigung b der linearen
7
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
Transformation, also b2 = 52 = 25, multipliziert. Es ergibt sich somit der Wert s2Y 0 = 52 × 9.82 =
245.5. Die Standardabweichung von Y 0 ergibt sich aus der Standardabweichung von Y durch
Multiplikation mit der Steigung b = 5, d. h. sY 0 = bsY = 5 × 3.13 = 15.65.
Bemerkungen: Eigentlich müsste das Quadrat der Standardabweichung sY 0 exakt mit der Varianz
s2Y 0 der transformierten Beobachtungen übereinstimmen. Das ist hier nicht der Fall und liegt
daran, dass wir s2Y und sY in Teilaufgabe 1) nur auf zwei Nachkommastellen genau bestimmt
hatten, also Rundungsfehler vorliegen, die aber vernachlässigbar klein sind. Beachten Sie, dass
die Steigung b bei der Berechnung von s2Y 0 quadriert wird, wogegen b bei der Berechnung der
Standardabweichung sY 0 nicht quadriert wird. Weiterhin gilt sY 0 = bsY nur dann, wenn die
Steigung b positiv ist. Bei einer negativen Steigung b ist die Formel sY 0 = |b|sY zu verwenden.
Der Betrag einer negativen Zahl ist die Zahl ohne das Vorzeichen, z. B. | − 3| = 3.
Die Spannweite und die Varianz sind anfällig gegenüber Ausreißern, während der Interquartilabstand
gegenüber Ausreißern robust ist.
Ausreißer beeinflussen das Minimum und/oder das Maximum der Beobachtungen in einem Datensatz
und wirken sich somit unmittelbar auf die Spannweite aus.
In die Berechnung der Varianz gehen alle Beobachtungen ein. Sehr große oder sehr kleine Beobachtungen, d. h. Ausreißer, liegen weiter vom Mittelwert entfernt als die typischen“ Beobachtungen in
”
einem Datensatz. Bei der Berechnung der Varianz werden diese großen Abweichungen quadriert. Ihr
Einfluss auf die Varianz wird dadurch noch verstärkt.
Die Berechnung des Interquartilabstands basiert auf dem unteren und dem oberen Quartil. Das untere
Quartil teilt den Datensatz im Verhältnis 1 zu 3 in Beobachtungen ein, die höchstens so groß bzw.
mindestens so groß wie das Quartil sind. Ausreißer mit kleinen Werten werden bei der Bestimmung
des unteren Quartils als Werte gezählt“, die zu den 25% der kleinsten Beobachtungen im Datensatz
”
gehören. Wie klein ein Ausreißer ist, spielt für die Berechnung des unteren Quartils bei größeren
Datensätzen keine Rolle. Entsprechend erkennt man, dass auch das obere Quartil nicht von Ausreißern
beeinflusst wird. Lediglich bei relativ kleinen Datensätzen können Ausreißer einen Einfluss auf die
Quartile und damit auf den Interquartilabstand ausüben.
8
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
4
Lösung zu Übung 4; Kap. 7
Die transformierten Werte sind in der folgenden Tabelle dargestellt (Messwerte, die in der Stichprobe
mehrfach auftauchen, sind hier nur einmal aufgeführt):
yi
48
51
55
57
60
62
65
zi
-1.75
-1.15
-.34
.06
.66
1.07
1.67
Zi
82.49
88.53
96.58
100.6
106.64
110.67
116.71
Ti
32.49
38.53
46.58
50.6
56.64
60.67
66.71
Zur Berechnung der Formel ist wie folgt vorzugehen:
Zunächst ist die Formel T = 50 + 10z nach z aufzulösen. Das Ergebnis kann nun in die Formel
Z = 100 + 10z eingesetzt werden. Es ergibt sich:
(T − 50)
10
Nach Vereinfachung erhält man die gewünschte Formel: Z = 50 + T
Z = 100 + 10
9
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
5
Lösung zu Übung 5; Kap. 7
1. Der Mittelwert der Beobachtungen ist ȳ = 1422/15 = 94.8. Der Modalwert ymod ist die Beobachtung, welche am häufigsten im Datensatz vorkommt. Im vorliegenden Fall tritt der Wert 97
dreimal auf, während alle anderen Werte seltener vorkommen. Also ist ymod = 97.
Der Median ymed wird mit Hilfe der Regel zur Bestimmung von Quantilen berechnet, da der
Median ja das 0.5-Quantil ist. Im ersten Schritt werden die Beobachtungen der Größe nach
angeordnet, was folgende Liste liefert:
79, 81, 82, 88, 91, 91, 95, 96, 97, 97, 97, 98, 100, 114, 116.
Im zweiten Schritt zur Bestimmung des p-Quantils wird das Produkt np aus dem Stichprobenumfang n und p berechnet. Hier ist n = 15 und speziell beim Median p = 0.5, d. h. np = 7.5.
Da np keine ganze Zahl ist, wird der Wert zu 8 aufgerundet. Der Median ist dann der (von links
gezählt) achte Werte in der Liste der geordneten Beobachtungen, also ymed = 96.
2. Der Mittelwert ist kleiner als der Median und der Median wiederum kleiner als der Modalwert,
d. h. ȳ < ymed < ymod . Aufgrund der Lageregeln kann die Verteilung der Beobachtungen als
(tendenziell) rechtssteil (linksschief) bezeichnet werden.
3. Zunächst wird die Fünf-Punkte-Zusammenfassung bestimmt. Danach wird geprüft, ob Ausreißer
oder Extremwerte vorliegen. Beim Vorhandensein von Ausreißern oder Extremwerten wird ein
modifizierter Box-Plot erstellt, andernfalls ein nicht modifizierter Box-Plot.
Aus der Liste der geordneten Beobachtungen in Teilaufgabe 1) kann direkt das Minimum ymin =
79 und das Maximum ymax = 116 der Beobachtungen abgelesen werden. Der Median ymed = 96
wurde in Aufgabenteil 1) bestimmt. Es fehlen also noch die beiden Quartile. Für das untere
Quartil y0.25 ist np = 15 × 0.25 = 3.75 keine ganze Zahl. Der Wert wird daher zu 4 aufgerundet.
Das untere Quartil ist dann an der vierten Position in der Liste der geordneten Beobachtungen
zu finden. Also gilt y0.25 = 88. Entsprechend ergibt sich als oberes Quartil y0.75 = 98.
Es ist nun zu überlegen, ob Ausreißer und/oder Extremwerte vorliegen. Ob eine Beobachtung
ein Ausreißer oder Extremwert ist, hängt davon ab, ob sie sehr weit vom unteren oder oberen
Quartil entfernt ist. Beobachtungen, die mindestens um das Anderthalbfache aber höchstens das
Dreifache des Interquartilabstands dQ kleiner als das untere Quartil sind bzw. die mindestens
um das Anderthalbfache aber höchstens das Dreifache von dQ größer als das obere Quartil sind,
werden im modifizierten Box-Plot separat als Ausreißer eingezeichnet. Als Symbol verwenden
wir beim Zeichnen einen Punkt. Beobachtungen, die noch weiter von den Quartilen entfernt
liegen, werden ebenfalls separat im modifizierten Box-Plot als Extremwerte eingezeichnet. Um zu
entscheiden, ob eine Beobachtung ein Extremwert ist, hat man festgelegt, dass die Extremwerte
mehr als das Dreifache des Interquartilabstands vom unteren bzw. oberen Quartil entfernt sein
müssen. Als Symbol für die Extremwerte verwenden wir einen Stern. Für den vorliegenden
Datensatz ist der Interquartilabstand dQ = y0.75 − y0.25 = 98 − 88 = 10. Es gibt genau zwei
Beobachtungen, die das Kriterium für Ausreißer erfüllen, nämlich die Werte 114 und 116, da
diese größer als y0.75 + 1.5dQ = 113 sind. Extremwerte kommen nicht vor.
Insgesamt ergibt sich der folgende Box-Plot.
10
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
4. Der Box-Plot kann wie folgt interpretiert werden: Der Median der Testergebnisse in der Stichprobe liegt beim Wert 96. Ausgehend von den Quartilen kann man erkennen, dass circa 50%
der Schüler ein Ergebnis zwischen den Werten 88 und 98 erreicht haben. Machen Sie sich dazu
klar, dass mindestens 25% der Beobachtungen höchstens so groß sind wie das untere Quartil
und mindestens 25% der Beobachtungen mindestens so groß sind wie das obere Quartil. Für den
Rest“ zwischen den beiden Quartilen bleiben also ungefähr 50% der Beobachtungen übrig.
”
Das niedrigste Testergebnis liegt beim Wert 79. Weiterhin liegen zwei Ausreißer mit hohen Testergebnissen vor. Bei der Datenanalyse würde man häufig zunächst prüfen, ob die Ausreißer
eventuell durch Eingabefehler (z.B. Tippen einer 114 statt einer 111) zustande gekommen sind.
Können Eingabefehler ausgeschlossen werden, würde man je nach Fragestellung eventuell untersuchen, ob die Schüler mit den hohen Testergebnissen vielleicht aus einer anderen Klassenstufe
kommen etc.
Die Verteilung der Daten erscheint rechtssteil. Das erkennt man daran, dass der Median sehr
nahe beim oberen Quartil liegt. Die Begründung dafür, dass ein nahe beim oberen Quartil
liegender Median auf eine rechtssteile Verteilung hindeutet lautet wie folgt: In dem kleinen
Bereich zwischen dem Median und dem oberen Quartil liegen ca. 25% der Daten, ebenso wie in
dem größeren Bereich zwischen Median und unterem Quartil.
In einem Histogramm würde sich dieser Sachverhalt so zeigen, dass die Säulen über den Klassen
im Bereich zwischen dem Median und dem oberen Quartil tendenziell höher sind als über den
Klassen im Bereich zwischen Median und unterem Quartil. Da dieser Bereich größer als der
Bereich zwischen dem Median und dem oberen Quartil ist, entsteht folglich der optische Eindruck
einer rechtssteilen und linksschiefen Verteilung.
Man gelangt also sowohl bei der Verwendung der Lageregel in Teilaufgabe 2) als auch der Verwendung des Box-Plots zur gleichen Beurteilung der Schiefe der Verteilung.
11
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
6
Lösung zu Übung 6; Kap. 8
1. Um die Kovarianz einer Variablen X mit einer anderen zu berechnen, kann man sich der folgenden
rechentechnisch günstigen Variante bedienen:
n
sxy =
1 X
xi yi − nx̄ȳ.
n−1
i=1
Nun ist die Kovarianz von X mit sich selbst von Interesse, y wird daher durch x ersetzt, d.h.
n
sxx
1 X 2
xi − nx̄2 .
=
n−1
i=1
Das ist wiederum die rechentechnisch günstige Variante der Varianz einer Variablen. Man kann
das auch ausgehend von der Definitionsformel der Kovarianz sehen:
sxx
n
n
i=1
i=1
1 X
1 X
=
(xi − x̄) (xi − x̄) =
(xi − x̄)2 = s2x .
n−1
n−1
Es fällt also auf, dass die Kovarianz einer Variablen mit sich selbst gleich der Varianz der Variablen ist. Wir berechnen also nun die Varianz unter Verwendung der rechentechnisch günstigen
Formel:
s2x = .10 × (903 − 11 × 54.22) = 30.66.
2. Unter
Pn Verwendung der rechentechnisch günstigen Formel für die Kovarianz, ergibt sich mit
i=1 xi yi = 381, x̄ = 7.364 und ȳ = 6.727 folgende Rechnung.
n
sxy =
1 X
xi yi − nx̄ȳ
n−1
i=1
sxy = .10 × (381 − (11 × 7.364 × 6.727)) = −16.39.
s
Die Korrelation ist rxy = sxxy
sy , so dass nur noch die Standardabweichungen der Variablen
−16.39
benötigt werden. Diese ergeben sich als sx = 5.54 und sy = 3.12, so dass rxy = 5.54×3.13
= −.945.
Dasselbe Ergebnisse hätte sich natürlich auch bei Anwendung derP
rechentechnisch günstigen Formel für die Korrelation ergeben, wenn man berücksichtigt, dass ni=1 yi2 = 596:
r=√
381 − 11 × 7.364 × 6.727
√
= −.945.
903 − 11 × 7.3642 596 − 11 × 6.7272
12
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
7
Lösung zu Übung 7; Kap. 8
1. Da die Beobachtungen in der Aufgabenstellung schon als Ränge vorliegen, kann der Rangkorrelationskoeffizient rs berechnet werden, indem man die Formel zu Berechnung der normalen“
”
Korrelation r auf die Daten anwendet. Da keine Bindungen vorliegen, kann hier auch die vereinfachte Formel angewendet werden:
P
6 × ni=1 d2i
6 × 34
rs = 1 −
=1−
= .794.
(n2 − 1)n
990
Man würde die Übereinstimmung zwischen den beiden Richtern hier als zufrieden stellend bewerten.
2. Da die Beurteilung des Schweregrads der Verbrechen mittels einer Rangreihe eine auf dem Niveau einer Ordinalskala gemessene Variable darstellt, kommen zur Beurteilung der Übereinstimmung der beiden Richter noch alle weiteren Assoziationsmaße für ordinale Variablen in Betracht.
Zusätzlich zur Rangkorrelation wurden die Koeffizienten γ (Gamma) und Kendalls τb (Tau-b)
behandelt. Diese beiden Koeffizienten basieren auf dem Konzept der konkordanten und diskordanten Paare, wobei bei τb zusätzlich noch die so genannten Bindungen berücksichtigt werden.
Zur Bestimmung der Anzahl C der konkordanten Paare, der Anzahl D der diskordanten Paare,
der Anzahl Tx der Paare mit Bindungen in X (Richter 1) und der Anzahl Ty der Paare mit
Bindungen in Y (Richter 2) sind insgesamt 10 × 9/2 = 45 verschiedene Paare von Zeilen in der
Tabelle zu betrachten. Es ergeben sich die folgenden Zahlen: C = 36, D = 9, Tx = 0, Ty = 0
und Txy = 0. Aus diesen Anzahlen berechnet man
γ=
und
C −D
36 − 9
=
= .6
C +D
36 + 9
C −D
36 − 9
√
p
= .6.
τb = √
=√
36 + 9 + 0 36 + 9 + 0
C + D + Tx C + D + Ty
3. Die Koeffizienten γ und τb stimmen überein. Das liegt daran, dass die Rangreihen der Richter
keine Bindungen enthalten. Die Koeffizienten γ und τb sind kleiner als der Rangkorrelationskoeffizient rs . Dieser Unterschied muss nicht verwundern, wenn man sich klar macht, dass die
Koeffizienten verschiedene Aspekte des Zusammenhangs erfassen.
13
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
8
Lösung zu Übung 8; Kap. 8
1. Zur Berechnung der Zusammenhangsmaße ist zunächst die Berechnung des χ2 -Wertes erforderlich:
Größe des Unternehmens
Fragebogen
Fragebogen nicht
ausgefüllt
ausgefüllt
klein
36
25
61
mittel
38
32
70
groß
28
41
69
102
98
200
Gesamt
Mit
Gesamt
k X
m
X
(nij − ñij )2
χ =
ñij
2
i=1 j=1
und ñij =
ni• n•j
n
ergibt sich der Wert:
χ2 =
61×102 2
2
2
(25 − 61×98
(38 − 70×102
200 )
200 )
200 )
+
+
61×102
61×98
70×102
200
200
200
69×102 2
69×98 2
2
(32 − 70×98
)
(28
−
)
(41
−
200
200
200 )
+
+
+
70×98
69×102
69×98
200
200
200
(36 −
= 4.87
und daraus
s
V =
χ2
=
n min(k − 1, m − 1)
r
4.87
= .16.
200 × 1
2. Cramers V beträgt .16 und deutet somit auf einen eher geringen Zusammenhang zwischen Unternehmensgröße und Ausfüllen des Fragebogens hin.
Zur Berechnung von K ∗ muss zunächst K bestimmt werden:
s
K=
χ2
=
2
χ +n
r
√
4.87
= .024 = .15
204.87
Der Korrigierte Kontingenzkoeffizient K ∗ beträgt dann mit Kmax =
p
1/2 = .71:
K ∗ = K/Kmax = .15/.71 = .21
K ∗ beträgt .21. Es fällt auf, dass sich die Ergebnisse für die beiden Zusammenhangsmaße unterscheiden. Dies verwundert nicht, da auch die Berechnungsvorschriften verschieden sind. Cramers
V ist bei 3 × 2-Tabellen generell gegenüber K ∗ vorzuziehen, weil nur V auch hier den maximalen
Fall von Eins annehmen kann.
3. Als geeignetes PRE-Maß ist hier λ heranzuziehen. Dazu benötigt man die Werte für Fehler1 und
Fehler2 :
Fehler1 = n•• − max n•j = 200 − 102 = 98.
j
14
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
Fehler2 =
k
X
(ni• − max nij ) = (61 − 36) + (70 − 38) + (69 − 41) = 85.
i
i=1
λ=
98 − 85
Fehler1 − Fehler2
=
= .13.
Fehler1
98
Durch Kenntnis der Unternehmensgröße kann die Vorhersage, ob ein Fragebogen ausgefüllt wurde oder nicht, um 13 Prozent verbessert werden im Vergleich zur Vorhersage ohne Kenntnis der
Unternehmensgröße.
15
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
9
Lösung zu Übung 9; Kap. 8
Als Maß der Beurteilerübereinstimmung empfiehlt sich Cohens κ. Zur Berechnung werden die Werte
auf der Hauptdiagonalen der Indifferenztabelle benötigt. Diese betragen:
n˜11 : 35×40
100 = 14,
n˜22 : 35×35
100 = 12.25,
n˜33 : 30×25
100 = 7.5
Im Anschluss können Pa und Pc berechnet werden:
Pa = (25 + 15 + 9)/100 = .49
Pc = (14 + 12.25 + 7.5)/100 = .3375
Daraus folgt:
κ=
0.49 − 0.3375
Pa − Pc
.1525
=
=
= .23
1 − Pc
1 − 0.3375
.6625
16
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
10
Lösung zu Übung 10; Kap. 9
Bei der Regression von Gewicht auf Körpergröße ergaben sich im SPSS-Output folgende fehlende
Werte:
1. SEE:
√
44.893 = 6.70025
Der Standardfehler
des Schätzers wird durch die Wurzel des Mittels der Quadrate der Residuen
√
SSE = M SE berechnet. Für den vorliegenden Fall schwanken die Gewichtswerte mit einer
Standardabweichung von 6.70 kg um die durch die Regressionsgleichung vorhergesagten Werte.
2. SSR : SST - SSE = 1703.6 - 359.146 = 1344.454
Dies ist die Summe der erklärten Abweichungsquadrate.
3. R2 : SSR /SST = 1344.454/1703.6 = .789
78.9 Prozent der Gesamtvariation des Gewichtes wird durch die Körpergröße erklärt.
√
4. R:+ .789 = .888, r=+.888
In diesem Beispiel korrelieren Gewicht und Körpergröße mit r=.888.
17
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
11
Lösung zu Übung 11 Kap. 10
1. ... die Mittelwerte betragen X̄1 = 4, X̄2 = 0.5, Ȳ = 5.125
2. ... die Varianzen betragen s2X1 = 7.429, s2X2 = 0.268, s2Y = 5.839
3. ... die Korrelationen betragen r(X1 , X2 ) = 0, r(X1 , Y ) = 0.260, r(X2 , Y ) = 0.608
4. ... der Determinationskoeffizient R2 der Regressionsgeraden Ŷ = a + b1 × X1 ist 0.068
5. ... der Determinationskoeffizient R2 der Regressionsgeraden Ŷ = a + b1 × X1 + b2 × X2 ist 0.438
18
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen
12
Lösung zu Übung 12 Kap. 10
1. Berechnen Sie die Regressionsgerade mit GS als Prädiktor und SQ als abhängiger Variablen.
b = 0.0534
a = 0.7332
2. Wie hoch ist der Determinationskoeffizient der Regressionsanalyse aus Teil 1?
R2 = 0.0155
3. Berechnen Sie den F -Wert für die Regressionsanalysen aus Teil 1.
F = 0.0155/(1-0.0155) * 694 = 10.944
4. Zu klären ist, ob es über den Zusammenhang zwischen GS und der Schulqualität hinaus noch
einen zusätzlichen Einfluss von M Q (also der Managementqualität) gibt. Bestimmen Sie hierfür
den inkrementellen Determinationskoeffizienten und den inkrementellen F-Wert für M Q gegeben
GS.
rSQ(M Q∗GS) = 0.525
2
rSQ(M
Q∗GS) = 0,2756
F = 0,2756 / ( (1- 0,2756 - 0,0155) / 693 ) = 269,4
19
Aus Holling/Gediga: Statistik – Deskriptive Verfahren © 2011 Hogrefe, Göttingen