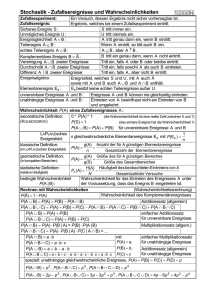
1 Grundlagen der Wahrscheinlichkeitsrechnung

Wahrscheinlichkeitsrechnung
1. Semester
Begleitendes Skriptum zur Vorlesung
im FH-Masterstudiengang
Technisches Management
von
Günther Karigl
FH Campus Wien 2016/17
Inhaltsverzeichnis
1. Semester: Wahrscheinlichkeitsrechnung
1 Grundlagen der Wahrscheinlichkeitsrechung
1.1 Ereignisse und Wahrscheinlichkeiten
1.2 Bedingte Wahrscheinlichkeit und Unabhängigkeit
2 Zufallsvariable und Verteilungen
2.1 Diskrete Verteilungen
2.2 Stetige Verteilungen
3 Spezielle Verteilungen und ihre Anwendungen
3.1 Alternativverteilung A(p)
3.2 Binomialverteilung B(n,p)
3.3 Hypergeometrische Verteilung
3.4 Poisson-Verteilung Po(λ)
3.5 Geometrische Verteilung Geo(p)
3.6 Normalverteilung N(µ,σ2)
3.7 Logarithmische Normalverteilung LN(µ,σ2)
3.8 Lebensdauerverteilungen
1
1
4
7
7
9
13
13
13
17
19
21
22
25
26
1 Grundlagen der Wahrscheinlichkeitsrechnung
1
1 Grundlagen der Wahrscheinlichkeitsrechnung
Die Wahrscheinlichkeitstheorie ist einerseits ein eigenständiges Teilgebiet der Mathematik,
anderseits kommt ihr aber auch eine wichtige Rolle als Bindeglied zwischen der deskriptiven
und der induktiven Statistik zu. Aufgabe der induktiven Statistik ist es ja, Verfahren
bereitzustellen, die Schlüsse von einer Stichprobe auf die zugehörige Grundgesamtheit
ermöglichen. Typische Problemstellungen der technischen Statistik sind etwa die
•
Kontrolle der Annahme bzw. der Auslieferung von Waren (Eingangs- bzw. Endkontrolle) in der statistischen Qualitätskontrolle, die
•
laufende Überwachung eines Produktionsprozesses, die
•
Untersuchung der Abhängigkeit der Qualität eines Produktes von bestimmten Produktionsfaktoren, oder die
•
Untersuchung des zeitlichen Verhaltens z.B. von Luftschadstoffen, usw.
Eine vollständige Überprüfung ist oft nicht möglich, z.B. dann, wenn es sich um eine
zerstörende Kontrolle handelt oder wenn diese mit hohen Kosten verbunden ist. Zudem zeigt
sich in der Praxis, dass oft auch infolge der Ermüdung des Kontrolleurs eine Überprüfung
mittels Stichproben einer vollständigen Kontrolle vorzuziehen ist.
Zur Beantwortung der eingangs gestellten Fragen wird man also in den allermeisten Fällen
eine Stichprobe ziehen und von dieser auf die entsprechende Grundgesamtheit rückschließen.
Hierzu muss allerdings erst ein geeignetes Modell für die Grundgesamtheit entwickelt
werden. Anstelle der empirischen Verteilungen der deskriptiven Statistik haben wir es in der
induktiven oder mathematischen Statistik mit theoretischen Verteilungen zu tun, die als
mathematische Modelle der Grundgesamtheit aufgefasst werden können. Die Wahrscheinlichkeitstheorie stellt nun theoretische Modelle für Grundgesamtheiten und Verteilungen von Merkmalen bereit, sie liefert Verfahren zur Schätzung von charakteristischen
Kenngrößen dieser Gesamtheiten und ermöglicht die Überprüfung von Annahmen über deren
Eigenschaften.
1.1 Ereignisse und Wahrscheinlichkeiten
In der Praxis tritt häufig das Bedürfnis auf, gewissen Ereignissen Wahrscheinlichkeiten
zuzuordnen, so z.B. dem
(i)
(ii)
Ereignis, mit einem Würfel die Zahl 6 zu würfeln, dem
Ereignis, dass ein aus einer Warenlieferung herausgegriffenes Stück „defekt“ im Sinn
der Lieferbedingungen ist, oder etwa dem
(iii) Ereignis, dass ein aus einer Produktion entnommenes Werkstück ein Bohrloch mit
einem Durchmesser zwischen 4,5 und 5,0 mm aufweist.
Dabei interessiert man sich stets für zufällige Ereignisse und nicht für deterministische
Erscheinungen.
1 Grundlagen der Wahrscheinlichkeitsrechnung
2
Physikalische Prozesse sind in der Regel, zumindest aus makroskopischer Sicht, in ihrem
Ablauf determiniert, d.h. vorhersagbar. Auch oftmalige Wiederholungen eines Experiments
führen innerhalb der Messgenauigkeit immer zum selben Ergebnis (z.B. für die Spannung U =
I⋅R im Gleichstromkreis). Im Gegensatz dazu besitzen Vorgänge im Bereich der Bio-, Sozialoder Wirtschaftswissenschaften häufig den Charakter von Zufallsexperimenten, d.h., ihr
Ausgang ist nicht vorhersehbar. Typische Beispiele von Zufallsexperimenten sind das Werfen
einer Münze oder eines Würfels, das Ziehen einer Spielkarte, das zufällige Auswählen einer
Person und Feststellen ihrer Körpergröße, ihres Blutdrucks oder ihres täglichen Zigarettenverbrauchs, u.v.a.m.
Jede einzelne Durchführung eines Zufallsexperiments heißt ein Versuch, sein Ergebnis ein
Versuchsausgang oder Elementarereignis. Alle Elementarereignisse eines Experiments
bilden zusammen den sogenannten Ereignisraum oder Stichprobenraum Ω. So gilt etwa für
die drei oben angegebenen Beispiele:
(i) Ω1 = {1,2,3,4,5,6}
(ii) Ω2 = {0,1,2,3, ...,n}, wo n den Umfang des Prüfloses bezeichnet
(iii) Ω3 = —+ = {x ∈ —x > 0}
Wie die Beispiele zeigen, gibt es Experimente mit endlichem oder unendlichem Stichprobenraum. Bei Größen- und Gewichtsmessungen beispielsweise sind die möglichen Ausgänge
zumeist beliebige positive Zahlen, also ist Ω = —+ die Menge aller positiven reellen Zahlen
oder Ω = [a, b] ein reelles Intervall.
Allgemein entspricht bei einem Zufallsexperiment einem Ereignis A eine Teilmenge A ⊆ Ω
und man sagt, A tritt genau dann ein, wenn eines der in A enthaltenen Elementarereignisse
eintritt. Enthält A dabei mehr als ein Elementarereignis, so heißt es zusammengesetzt. So ist
z.B. das Würfeln einer geraden Augenzahl ein zusammengesetztes Ereignis, nämlich
zusammengesetzt aus den Elementarereignissen, die den Augenzahlen 2, 4 und 6 entsprechen:
A = {2,4,6}. Insbesondere ist auch Ω selbst ein Ereignis, welches bei jeder Versuchsausführung eines Zufallsexperiments eintritt und deshalb das sichere Ereignis genannt wird.
Ferner ist es zweckmäßig, die leere Menge als Ereignis ∅ zuzulassen, das keinem möglichen
Ausgang entspricht und daher auch unmögliches Ereignis heißt.
Ereignisse können zu neuen Ereignissen kombiniert werden. Sind A,B ⊆ Ω Ereignisse, so
erhält man durch Anwendung der mengentheoretischen Operationen der Durchschnitts-,
Vereinigungs- und Differenzenbildung die weiteren Ereignisse A ∩ B, A ∪ B und A \ B,
welche als „A und B“, „A oder B“ bzw. „A aber nicht gleichzeitig B“ bezeichnet werden. Zu
jedem A kann daher insbesondere auch A = Ω \ A, das komplementäre Ereignis zu A,
gebildet werden. Ferner heißen zwei Ereignisse A und B unvereinbar (oder disjunkt), wenn
A ∩ B = ∅ gilt.
Alle Ereignisse eines Zufallsexperiments bilden eine so genannte Ereignisalgebra oder σAlgebra, das ist ein nicht leeres System Σ von Teilmengen A, B, C, ... von Ω mit den
Eigenschaften
A ∈ Σ ⇒ A ∈ Σ,
A1 , A 2 ,... ∈ Σ ⇒ A1 ∪ A 2 ∪ ... ∈ Σ.
D.h., Σ ist gegenüber der Komplementbildung sowie der Vereinigung von endlich oder
abzählbar unendlich vielen Ereignissen abgeschlossen.
1 Grundlagen der Wahrscheinlichkeitsrechnung
3
Wir greifen nochmals auf das einfache Zufallsexperiment „Werfen eines Würfels“ zurück und
stellen uns die Frage: Wie groß ist die Wahrscheinlichkeit dafür, dass ein bestimmtes
Ereignis, z.B. eine gerade Augenzahl auftritt? Um die Wahrscheinlichkeit P(A) eines
Ereignisses A festzulegen, gab es historisch gesehen verschiedene Zugänge:
•
Wir betrachten unter allen möglichen Ausgängen des Experiments diejenigen, bei
denen das Ereignis A eintritt. Je größer die Anzahl dieser für A günstigen Fälle ist,
desto wahrscheinlicher wird A eintreten. Es ist daher naheliegend, den Anteil der für
A günstigen Ausgänge an allen insgesamt möglichen Ausgängen des Zufallsexperiments als die Wahrscheinlichkeit P(A) des Ereignisses A zu bezeichnen. Die so
genannte klassische Definition der Wahrscheinlichkeit P(A) eines Ereignisses A für
ein Zufallsexperiment mit endlich vielen gleichwahrscheinlichen Ausgängen (ein so
genanntes Laplace-Experiment) lautet dann
P(A) =
Anzahl der für A günstigen Ausgänge
.
Anzahl der insgesamt möglichen Ausgänge
Aus dieser Definition folgt übrigens sofort, dass stets 0 ≤ P(A) ≤ 1 gilt. Insbesondere
ist P(∅) = 0 und P(Ω) = 1. Die Antwort auf die oben gestellte Frage nach der Wahrscheinlichkeit dafür, dass beim Ausspielen eines Würfels eine gerade Augenzahl
auftritt, ist nun leicht zu finden: Von den sechs möglichen Augenzahlen sind drei,
nämlich eben die geraden Zahlen, für das betrachtete Ereignis A günstig, d.h. P(A) =
3/6 = 1/2.
•
Sind die Voraussetzungen für ein Laplace-Experiment nicht erfüllt, so kann man die
Wahrscheinlichkeit P(A) eines Ereignisses A so festlegen, dass man das Zufallsexperiment n-mal durchführt und die relative Häufigkeit hn(A) für das Auftreten von
A betrachtet. Strebt die Folge hn(A) für n = 1,2,3,... dann einem festem Wert zu, wählt
man in naheliegender Weise
P(A) = lim h n (A)
n →∞
bzw. in der Praxis P(A) ≈ hn(A) für großes n. (Tatsächlich gilt nach dem so genannten
Gesetz der großen Zahlen von Bernoulli, dass hn(A) „fast sicher“ gegen P(A)
konvergiert.) Sind etwa laut Geburtenstatistik unter 4255 Neugeborenen eines Jahres
in einer Geburtsklinik 2183 Knaben und 2072 Mädchen, wird man die Wahrscheinlichkeit für die Geburt eines Knaben mit P(K) = 2183/4255 = 0,513 und für die
Geburt eines Mädchens mit P(M) = 2072/4255 = 0,487 festsetzen.
Heute ist es allerdings üblich, den Begriff der Wahrscheinlichkeit rein axiomatisch festzulegen. Eine Wahrscheinlichkeit ist demnach eine Funktion P: Σ → —, die jedem Ereignis A
aus einer Ereignisalgebra Σ über dem Ereignisraum Ω eine reelle Zahl P(A) zuordnet, wobei
folgende Bedingungen erfüllt sind:
1. 0 ≤ P(A) ≤ 1 für alle Ereignisse A
2. P(Ω) = 1
3. P(A ∪ B) = P(A) + P(B) für disjunkte Ereignisse A und B bzw.
P(A1 ∪ A2 ∪ ...) = P(A1) + P(A2) + ... falls die Ereignisse Ai paarweise disjunkt sind
1 Grundlagen der Wahrscheinlichkeitsrechnung
4
Das sind die Wahrscheinlichkeitsaxiome von Kolmogoroff. Das dritte Axiom wird auch als
Additionssatz für disjunkte Ereignisse bezeichnet. Jede Funktion P, die diese Axiome erfüllt,
heißt ein Wahrscheinlichkeitsmaß oder kurz Wahrscheinlichkeit.
Aus den Axiomen lassen sich für das praktische Rechnen mit Wahrscheinlichkeiten sofort
einige einfache Folgerungen ableiten, die wir im Folgenden zusammenfassen.
4. P(∅) = 0
5. P( A ) = 1 − P(A)
6. A ⊆ B ⇒ P(A) ≤ P(B)
7. P(A ∪ B) = P(A) + P(B) − P(A ∩ B) Additionssatz für zwei beliebige Ereignisse
Der zuletzt angeführte Additionssatz gilt für beliebige Ereignisse A und B im Gegensatz zum
Additionssatz in Axiom 3., welches nur für disjunkte Ereignisse gültig ist. Im Übrigen kann
man zeigen, dass der klassische Wahrscheinlichkeitsbegriff als Spezialfall für ein Zufallsexperiment mit endlich vielen gleichwahrscheinlichen Ausgängen im Axiomensystem von
Kolmogoroff enthalten ist, so dass sich der axiomatische Wahrscheinlichkeitsbegriff als eine
echte Verallgemeinerung des klassischen erweist.
1.2 Bedingte Wahrscheinlichkeit und Unabhängigkeit
In vielen Fällen wird die Wahrscheinlichkeit P(A) für das Eintreten eines Ereignisses A
dadurch verändert, dass ein anderes Ereignis B bereits eingetreten ist. Diese neue Wahrscheinlichkeit für das Eintreten von A unter der Bedingung B wird dann die durch B bedingte
Wahrscheinlichkeit von A genannt und mit P(AB) bezeichnet. Ist P(B) = 0, so gilt dann
klarerweise auch P(AB) = 0, für P(B) ≠ 0 dagegen ergibt sich ihr Wert aus der Formel
P(AB) =
P(A ∩ B)
.
P(B)
Aus dieser Definition der bedingten Wahrscheinlichkeit folgt sofort der Multiplikationssatz
für zwei beliebige Ereignisse A und B:
P(A ∩ B) = P(AB) P(B) = P(A) P(BA),
Der Multiplikationssatz kann von zwei Ereignissen auf n ≥ 2 Ereignisse wie folgt verallgemeinert werden (der Beweis erfolgt durch vollständige Induktion):
P(A1 ∩ A2 ∩ A3 ∩ ... ∩ An) = P(A1) P(A2A1) P(A3A1∩A2) ... P(AnA1∩ ... ∩An−1).
Mit dem Multiplikationssatz verbunden ist der Begriff der Unabhängigkeit von Ereignissen:
Die beiden Ereignisse A und B heißen unabhängig, falls
P(A ∩ B) = P(A) P(B)
5
1 Grundlagen der Wahrscheinlichkeitsrechnung
bzw. gleichwertig dazu, falls P(AB) = P(A) oder (wegen der Symmetrie der Unabhängigkeitsbedingung in A und B) auch falls P(BA) = P(B).
Beispiel: Werfen eines Würfels, Ω = {1,2,3,4,5,6}
•
A = {6} (Würfeln eines Sechsers), B = {2,4,6} (gerade Zahl)
P(A) = 1/6, P(B) = 1/2, P(AB) = 1/3, A und B sind abhängig
•
A = {1,2} (Augenzahl höchsten 2), B = {2,4,6} w.o.
P(A) = 1/3, P(B) = 1/2, P(A∩B) = 1/6 = P(A) P(B), A und B sind unabhängig
In der Praxis hat man zur Ermittlung der Wahrscheinlichkeit P(A) sehr oft eine Fallunterscheidung durchzuführen, welche einer disjunkten Zerlegung Ω = B1 ∪ B2 ∪ ... ∪ Bn des
Ereignisraums entspricht. Sind die Wahrscheinlichkeiten P(Bi) und die bedingten Wahrscheinlichkeiten P(ABi) für alle i bekannt, dann kann P(A) wie folgt ermittelt werden:
A = A ∩ Ω = (A ∩ B1 ) ∪ ... ∪ (A ∩ Bn ) ⇒
P(A) = P(A ∩ B1 ) + ... + P(A ∩ Bn )
= P(A | B1 )P(B1 ) + ... + P(A | Bn )P(Bn ),
also
n
P(A) = ∑ P(A | Bi )P(Bi ) ,
i =1
was auch der Satz von der totalen Wahrscheinlichkeit genannt wird.
Beispiel: Zur Chipproduktion werden drei Maschinen eingesetzt. Die Maschine M1 deckt 50%
der Gesamtproduktion ab und liefert 3% Ausschuss. Auf die Maschine M2 entfallen 30% der
Produktion bei einem Ausschussanteil von 1%, während die Maschine M3 20% der
Produktion bei einem Ausschussanteil von 2% bestreitet. Gesucht ist die Wahrscheinlichkeit
dafür, dass ein zufällig der Produktion entnommenes Stück defekt ist.
Bezeichnen wir mit A das Ereignis, dass ein fehlerhaftes Stück produziert wurde und mit Mi
das Ereignis, dass ein beliebig ausgewähltes Stück aus der Produktion der Maschine Mi
stammt (für i = 1,2,3). Dann gilt
P(A) = P(A | M1 )P(M1 ) + P(A | M 2 )P(M 2 ) + P(A | M 3 )P(M 3 )
= 0, 03 ⋅ 0, 5 + 0, 01 ⋅ 0, 3 + 0, 02 ⋅ 0, 2 = 0, 022.
Somit beträgt die gesuchte Wahrscheinlichkeit, also der Ausschussanteil insgesamt 2,2%.
Ein einfache Folgerung aus dem Satz von der totalen Wahrscheinlichkeit ist die so genannte
Bayes’sche Formel: Ist Ω = B1 ∪ B2 ∪ ... ∪ Bn eine disjunkte Zerlegung des Ereignisraums
und A ein beliebiges Ereignis, so gilt nach Definition der bedingten Wahrscheinlichkeit
P(B1 | A) =
P(B1 ∩ A) P(A | B1 )P(B1 )
P(A | B1 )P(B1 )
=
= n
,
P(A)
P(A)
∑ P(A | B j )P(B j )
j=1
6
1 Grundlagen der Wahrscheinlichkeitsrechnung
bzw. allgemein für alle i = 1,...,n
P(Bi | A) =
P(A | Bi )P(Bi )
n
∑ P(A | B )P(B )
j=1
j
.
j
Von der Aufgabenstellung her kann man dabei die Ereignisse B1, B2, ...,Bn oft als mögliche
Ursachen für das Ereignis A deuten. Ist nun das Ereignis A tatsächlich eingetreten, so lässt
dies dann Rückschlüsse auf die möglichen Ursachen zu, indem deren a priori Wahrscheinlichkeiten P(Bi) sich damit a posteriori (nämlich durch das Eintreten von A) zu P(BiA)
ändern.
Beispiel: Wir betrachten nochmals den Produktionsprozess auf den drei Maschinen M1, M2
und M 3 des vorhergehenden Beispiels. Unter der Annahme, dass ein produziertes Stück
fehlerhaft ist, wie groß ist dann nachträglich die Wahrscheinlichkeit, dass es von einer der
Maschinen Mi, i = 1,2,3, stammt?
Zur Beantwortung dieser Frage verwenden wir die Bayes’sche Formel und erhalten
P(M 1 | A) =
P(A | M 1 )P(M 1 ) 0,03 ⋅ 0,5
=
= 0,68 ,
P( A )
0,022
P(M 2 | A) =
P(A | M 2 )P(M 2 ) 0,01 ⋅ 0,3
=
= 0,14 ,
P( A )
0,022
P(M 3 | A) =
P(A | M 3 )P(M 3 ) 0,02 ⋅ 0,2
=
= 0,18 .
P(A)
0,022
Wie nicht anders zu erwarten, hat sich diese Wahrscheinlichkeit für die Maschine M1 mit
einem relativ hohen Ausschussanteil gegenüber der a priori Wahrscheinlichkeit von 0,5
erhöht, dagegen sind die Wahrscheinlichkeiten für die Maschinen M2 und M3 als mögliche
„Ursachen“ für den Fehler jeweils zurückgegangen.
M1
M2
M3
a priori
50%
30%
20%
100%
a posteriori
68%
14%
18%
100%