Document

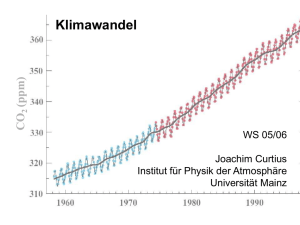
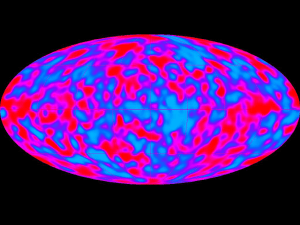
CMB
Echo des
Urknalls
Max Camenzind
Februar 2015
Lemaître 1931: Big Bang des
expandierenden Universums
Big Bang :
 Photonenhintergrund
+ Neutrinohintergrund
3-Raum
expandiert:
dx  a(t) dx ;
Wellenlängen
werden ebenso
gestreckt.
Unsere Themen
•
•
•
•
•
Geschichte des Universums und CMB
Gleichgewicht von Strahlung und Materie
Die Rekombination  CMB als Relikt
CMB-Strahlung – Historie
Reminiszenz: Was ist ein Schwarzer
Körper?
•  Plancksches Strahlungsgesetz
•  Wiensches Verschiebungsgesetz
•  Photon-Baryon Verhältnis im Universum
Was ist Rekombination ?
Unter Rekombination versteht man die
Vereinigung positiver und negativer
Ladungsträger ( Ionen + Elektronen ) zu
einem elektrisch neutralen Produkt (Atom
oder Molekül ).
 Rekombination stellt den Umkehrprozess zur Ionisation dar.
Rekombination
Big Bang
t = 0:
Rand des
Universums
.
.
.
.
.
.
.
.
.
.
.
Strahlungssphäre:
Photon-dominiertes
neutrales Plasma
1 e- auf 2 Mrd. Phot
.
.
Photosphäre
Universum
2,725 K
380.000 LJ
.
Temperatur
nimmt zu
T  1032 K
.
.
.
Von Rekombination zu Reionisation
Kaltes Gas
1
0.1
0.01
Dunkles
Zeitalter
0.001
Big Bang Nukleosynthese & CMB
• 1940s: Gamow,
Alpher & Herman:
alle chemischen
Elemente werden
synthetisiert via
nukleare Reaktionen
“in hot early universe
 ylem”
•  1. Vorhersage der
Existenz des CMB mit
T0 ~ 5 K
George Gamow (1904-1975)
Die Entdeckung der 3K-Hintergrundstrahlung
1964 entdeckten die beiden Radio Ingenieure Arno Penzias und Robert
Wilson bei der Eichung einer Antenne ein Strahlungssignal im
Mikrowellenlängenbereich ( = 7,15 cm).
Da dieses Signal keine periodischen Schwankungen zeigte und aus allen
Richtungen in gleicher Stärke kam, schien es kosmischen Ursprungs zu
sein.
Beide erhielten
1978 den
Nobelpreis für
ihre Entdeckung.
Robert Dicke
ging leer aus.
Photo: Physics Today
Arno Penzias und Robert Wilson entdecken mit ihrer
neuentwickelten Hornantenne ein isotropes Rauschen mit
λ≈7,15cm, konnten es nicht erklären. Robert Dicke (Princeton)
identifiziertes es als CMB. Penzias + Wilson Nobelpreis, 1978
Spektrum der 3K Strahlung  Planck
T0 = 2,725 K
Was ist Wiensches
Verschiebungsgesetz ?
??????????????
Ein bisschen Allgemeinwissen:
Wovon hängt die Energieverteilung
der Planckschen Strahlung ab?
Wann wurde das Gesetz gefunden?
Max Planck 1900
Wirkungsquantum h
h = 4,1 x 10-15 eV s
Der Schwarze Körper
 Planck postuliert h 1900
Absorbiert sämtliche Strahlung
 Keine Transmission oder Reflexion
 Thermische Emission mit bestimmter
Intensität und spektraler Verteilung

Plancksches
Strahlungsgesetz:
Wie sieht die EnergieVerteilung u() aus?
u()?
1900: Plancks grundlegende
Annahme  Oszillatoren
im Hohlraum nur diskrete Frequ
E  h 
Planksche Wirkungsquantum:
h  (6,6256  0,0005) 10
27
Js
Energie  Zeit
Spektrum eines Schwarzen Körpers
2
1
B  2 2 h
c
exph / k BT   1
F  B (T )
Ein Photon hat
2 PolarisationsFreiheitsgrade
QuantenZustandsDichte
PhotonEnergie
Zustands-BesetzungsGrad
(Quanten-Statistik)
Dies geht nur, wenn man Licht als Energie-Quanten mit Energie hν
betrachtet. Dies hat Max Planck 1900 entdeckt als er, eher widerwillig,
versuchte, die Schwarzkörperstrahlung mit der Boltzmannschen Statistik
zu beschreiben, obwohl er am Anfang gar nicht glaubte, dass seine
Quanten wirklich physikalische Bedeutung hatten. Er hat damit,
unwillkürlich, die Geburt der Quantenmechanik eingeläutet.
Plancksches Strahlungsgesetz
• ein schwarzer Körper der Temperatur T
emittiert Strahlung der Frequenz  mit der
Intensität  2 Naturkonstanten: h und k
2h
1
B (T )  2 h / kT
.
c e
1
3
• Max Planck (1900): Energie kann nur
gequantelt abgegeben bzw. aufgenommen
werden (sonst  „UV-Katastrophe”).
 Plancksches
Strahlungsgesetz
h max = 2,8 kT
2h
1
B (T )  2 h / kT
.
c e
1
3
Spektrum eines Schwarzen Körpers
( h  k BT )
2h 3
1
2 2
B  2

k BT
2
c exph / k BT   1
c
Rayleigh-Jeans Limit
Bei niedrigen Frequenzen stimmt
das Rayleigh-Jeans Gesetz
(klassische Beschreibung)
Bei hohen Frequenzen (=Energien)
muss man Quanten-Statistik
anwenden, sonst erfolgt die
Ultraviolett-Katastrophe
T = 300 K
 … nur von Temperatur T
~ 1/4
Staub
Emission eines Schwarzen Strahlers
Das Integral über die Planck-Kurve gibt den totalen
(=bolometrischen) Fluss:


0
0
F   F d    B (T )d   SBT
Temperatur:
T
F  B (T )
F   SBT
4
4
Watt
m 2  Hz
Watt
m2
Sterne als Schwarze Körper
Als erste Annäherung können wir Sterne als Schwarzkörper betrachten
d
R*
Fluss an der Oberfläche:
F  B (T* )
Luminosität:
L  4 2 R*2 B (T* )
Beobachteter Fluss:
2
 R* 
F    B (T* )
d 
Photon-Baryon Verhältnis Universum
Heutige Dichte der Baryonen
Photonen erfüllen Bose-Einstein Verteilung
z(3) = 1.33
 Photon-Baryon Verhältnis mit WBh² = 1.6 x 109
 Es gibt viel mehr Photonen als Baryonen im
Universum
Beitrag CMB zur Expansion ?
Nach Stefan-Boltzmann:
 Energiedichte = aSB T4
aSB = 7,56 x 10-16 J/m³/K4
 WRad = 9 x 10-5 (mit Neutrinos)
 Da Druck PRad = Endichte/3
 dominant im frühen Universum