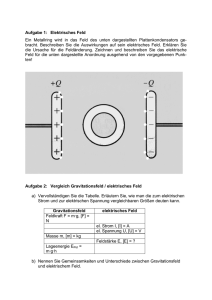
Ladungen und elektrisches Feld

Ladungen und elektrisches Feld
Physik–Sp
1) Welche Ladung ist durch den Leiterquerschnitt geflossen, wenn eine konstante Stromstärke
I = 1, 8 mA 5 min und 12 s lang gemessen wird?
2) Eine Batterie kann eine Ladung von 88 Ah abgeben. Wie lange kann man ihr einen Strom von
0, 5 A entnehmen?
3) Berechnen Sie die elektrische Feldstärke an einem Ort, an dem auf einen Körper mit einer
Ladung Q = 26 nC die Kraft F = 37 µN wirkt.
4) Berechnen Sie die Kraft, die ein Körper mit einer Ladung Q = 78 nC in einem Feldpunkt der
Feldstärke E = 810 kN
erfährt.
C
5) Die Feldlinien eines Plattenkondensators verlaufen vertikal von unten nach oben. Ein im
Plattenraum eingebrachtes positiv geladenes Öltröpfchen, dessen Masse m = 4, 7 · 10−10 kg
ist, schwebt gerade. Messungen ergeben eine Feldstärke E = 7, 2 GN
.
C
Berechnen Sie die Ladung des Öltröpfchens.
sei senkrecht zur Erdoberfläche nach unten gerichtet.
6) Ein elektrisches Feld der Stärke 180 N
C
Vergleichen Sie die nach oben gerichtete elektrostatische Kraft auf eine Elektron
(q = 1, 6 · 10−19 C, m = 9, 1 · 10−31 kg) mit der nach unten gerichteten Gravitationskraft
(g = 9, 81 sm2 ).
Wie stark müsste eine 3 g schwere Münze geladen sein, damit die durch dieses Feld bewirkte
elektrostatische Kraft die Gravitationskraft ausgleicht?
7) Begründen Sie: Das Innere eines hohlen Metallkörpers enthält im elektrostatischen Gleichgewicht weder ein elektrisches Feld noch überschüssige Ladungen.
8) Eine Pendelkugel ist mit einer Ladung Q = 52 nC geladen und hat die
Masse m = 0, 40 g. Sie hängt an einem Faden der Länge l = 1, 80 m
in einem horizontal gerichteten homogenen elektrischen Feld. Durch die
Kraft des Feldes wird sie um d = 15 mm ausgelenkt. Wie groß ist die
Feldstärke E des homogenen Feldes?
α
l
Tipp: Wegen der geringen Auslenkung ist die Rückstellkraft des Pendels
quasi parallel zum elektrischen Feld.
d
FR
α
Fg
Ladungen und elektrisches Feld
Physik–Sp
Lösungen
1) Q = I · t = 1, 8 mA · 312 s = 561, 6 mC
2) Q = 88 Ah= 316 800 C;
3) E =
t=
Q
= 633 600 s = 176 h
I
kN
F
= 1, 4
Q
C
4) F = Q E = 63 mN
5) Fg = Fel
⇒
mg = QE
6) Fel = 2, 88 · 10−17 N;
Fg = Fel
⇒
⇒
Q=
mg
= 6, 4 · 10−19 C
E
Fg = 8, 936 · 10−30 N;
mg = QE
⇒
Q=
Fel
= 3, 2 · 1012
Fg
mg
= 163, 5 µC
E
7) chisum
8) Rückstellkraft FR = Fg · sin α = m g sin α
Auslenkung d = l · sin α
FR ||Fel
⇒
⇒
mgd
= qE
l
sin α =
⇒
E=
d
= 0, 47◦
l
mgd
ql
⇒
FR =
= 628, 85
mgd
= 3, 27 · 10−5 N
l
α
l
N
C
d
FR
α
Fg