Theoretische Physik: Mechanik

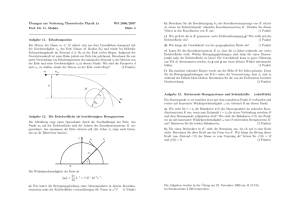
RWTH Aachen
Institut für Theoretische Physik
Physikzentrum Melaten
Aachen, den 27. Oktober 2006
Bau 26C, 4. Stock
Theoretische Physik: Mechanik
2. Übung
Aufgabe 4
a) Ein Fluss der Breite d = 500m ieÿt auf der Nordhalbkugel der Erde ( 0 ≤ θ ≤ π2 )
mit der Geschwindigkeit v0 = 6km/h nach Süden. Bestimmen Sie den auf Grund der
Corioliskraft auftretenden Unterschied zwischen dem Wasserstand des westlichen und
östlichen Flussufers in Abhängigkeit von der geographischen Breite φ. Betrachten Sie
insbesondere den Fall φ = 30◦ . Benutzen Sie bei der Herleitung Kugelkoordinaten mit
θ = π2 − φ.
b) Auf der Erdoberäche werde in einem Punkt der geographischen Breite φ ein kartesisches Koordinatensystem angebracht mit den Achsen 3 nach oben, 1 nach Osten und 2
nach Norden. Berechnen Sie die auf Grund der Corioliskraft auftretende Ostabweichung,
falls aus der Höhe H zur Zeit t = 0 ein Massenpunkt fallen gelassen wird. Hierbei wird
vorausgesetzt, dass sich die Ortskoordinaten in 1- und 2-Richtung während des Falls nur
wenig ändern. Als numerisches Beispiel wähle man H = 200m und φ = 40◦ , wobei die
Winkelgeschwindigkeit der Erde gegeben ist durch ω = 7.3 · 10−5 s−1 .
Aufgabe 5
a) Wie hängt die auf eine auf der Erdoberäche ruhende Masse m wirkende Trägheitskraft
(welche?) von der geographischen Breite φ (siehe Aufgabe 4 a)) ab? Berücksichtigen Sie
dabei nur die Erdrotation und wählen Sie ein geeignetes Inertialsystem (Skizze).
b) Welche Beschleunigung ~a = ~a(r) erfährt ein Massenpunkt, der sich in einer Ebene auf
einer logarithmischen Spirale (Skizze)
r = a e−αϕ
(a, α = const.)
mit konstanter Winkelgeschwindigkeit ω zum Zentrum bewegt? Wie lässt sich die zugehörige Kraft interpretieren?
Abgabe:
03.11.2006 in den Übungen