Bewegungen – Kinematik Gleichförmige geradlinige Bewegung
Werbung
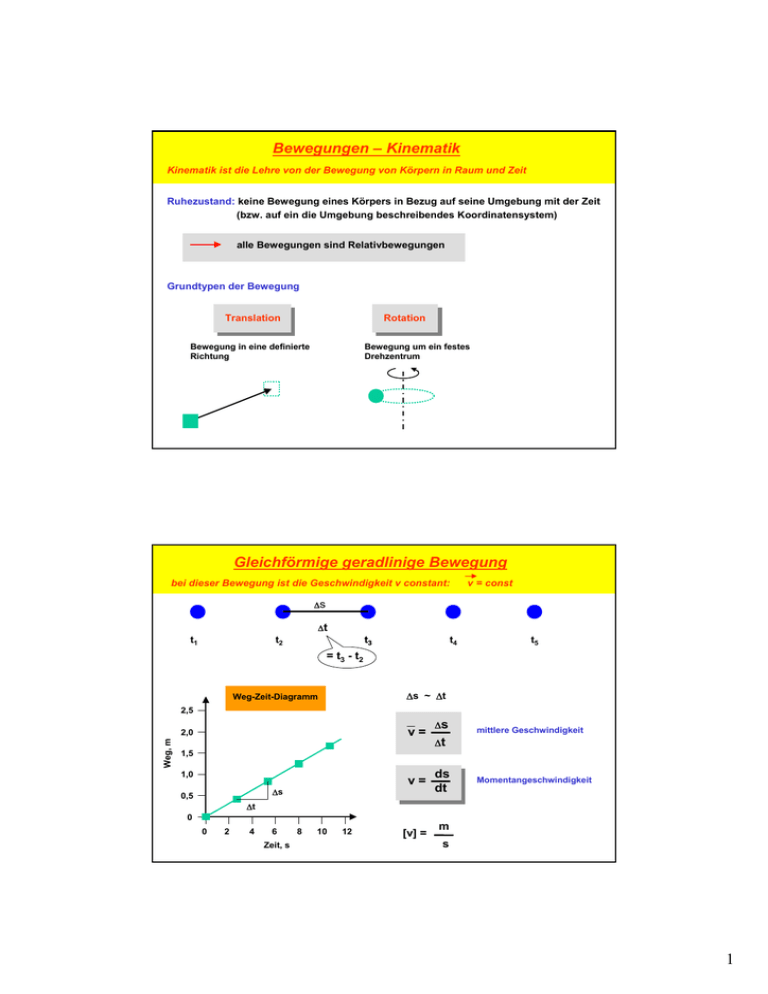
Bewegungen – Kinematik Kinematik ist die Lehre von der Bewegung von Körpern in Raum und Zeit Ruhezustand: keine Bewegung eines Körpers in Bezug auf seine Umgebung mit der Zeit (bzw. auf ein die Umgebung beschreibendes Koordinatensystem) alle Bewegungen sind Relativbewegungen Grundtypen der Bewegung Translation Rotation Bewegung in eine definierte Richtung Bewegung um ein festes Drehzentrum Gleichförmige geradlinige Bewegung bei dieser Bewegung ist die Geschwindigkeit v constant: v = const ∆s ∆t t1 t2 t3 t4 t5 = t3 - t2 ∆s ~ ∆t Weg-Zeit-Diagramm 2,5 v= Weg, m 2,0 ∆s mittlere Geschwindigkeit ∆t 1,5 1,0 v= ∆s 0,5 ds dt Momentangeschwindigkeit ∆t 0 0 2 4 6 Zeit, s 8 10 12 [v] = m s 1 Gleichmäßig beschleunigte Bewegung hier ist die Beschleunigung a constant: a = const 0 1 2 0 0,5 3 2 4,5 2,5 2 5 8 18 4,5 5,5 Zeit, s Weg, cm v, cm/s ∆v ~ ∆t 16 a= 12 ∆v ∆t mittlere Beschleunigung ∆v 8 ∆t a= 4 0 6 12,5 3,5 20 6 Weg, cm mittl. Geschwindigkeit, cm/s 0,5 1,5 4 4 0 0 1 2 3 4 5 6 [a] = Zeit, s dv dt Momentanwert der Beschleunigung m s2 Freier Fall frei fallende Körper werden zum Erdmittelpunkt hin beschleunigt ein frei fallender Körper bewegt sich gleichmäßig beschleunigt (bei Vernachlässigung von Reibungskräften und Luftwiderstand) g = 9,81 m s-2 Fallbeschleunigung Weg – Zeit – Gesetz s = ½ g t2 Geschwindigkeit – Zeit – Gesetz Berechnung der Fallzeit für einen Körper aus h = 30 m t = √2h/g t = 2,47 s Berechnung der Geschwindigkeit, mit der der Körper aus 30 m Höhe auf den Erdboden prallt v = gt v = 24,2 m/s 2 Diagramme und Gesetze gleichförmig geradlinige Bewegung gleichmäßig beschleunigte Bewegung Weg-Zeit-Diagramm Geschw.-Zeit-Diagramm s t t t Weg-Zeit-Gesetze Beschl.-Zeit-Gesetze Geschw.-Zeit-Gesetze s = v0t s= Beschl.-Zeit-Diagramm a v a0 t2 2 v = v0 a=0 v = a0t a = a0 Gleichförmige Kreisbewegung bei dieser Bewegung ist die Winkelgeschwindigkeit ω constant: ω = const ∆t = t2 - t1 t2 ∆ϕ M r ∆ϕ ~ ∆t t1 ω = ∆ϕ ∆t mittlere Winkelgeschwindigkeit Der Winkel wird in Bogenmaß gemessen! Bogenmaß = Bogenlänge b Radius Gradmaß r Bogenmaß 360º 2πr / r = 2π 180º π 90º π/2 ω = dϕ dt Winkelgeschwindigkeit [ ω ] = s-1 bzw. rad s-1 Radiant (rad) ist eine Zählgröße für Winkel (Bogenmaß) 3 Gleichförmige Kreisbewegung Bahn- und Winkelgeschwindigkeit sind einander proportional v2 ∆s Winkelgeschwindigkeit, Kreisfrequenz v = ds/dt Bahngeschwindigkeit t2 ∆ϕ M ω = dϕ/dt v1 dϕ = ds/r t1 r v r ω = Periodendauer (oder Umlaufzeit) T v = ωr T=2π/ω Zeit für das Überstreichen des Winkels 2π f=ω/2π f=1/T Frequenz (oder Umdrehungszahl) f ω=2πf Gleichförmige Kreisbewegung jede Kreisbewegung ist eine beschleunigte Bewegung v2 ω: Winkelgeschwindigkeit, Kreisfrequenz ∆v - v1 v: Bahngeschwindigkeit v1 ∆v = M v2 - v1 ∆v ist bei ∆t → 0 zum Kreismittelpunkt gerichtet ar = dv dt ar = ω2 r Radialbeschleunigung ar = v2 r der Vektor der Radialbeschleunigung ist stets zum Kreismittelpunkt gerichtet 4 Ungleichförmige Kreisbewegung bei dieser Kreisbewegung ändert sich die Winkelgeschwindigkeit ω ≠ const α= ω v α= ∆ω ∆t dω Winkelbeschleunigung dt r [ α ] = s-2 die Winkelgeschwindigkeit ω ist ein axialer Vektor zwei Einstellungen von ω parallel zur Drehachse je nach Drehsinn Harmonische ungedämpfte Schwingung periodische Vergänge können auch als Schwingung beschrieben werden Schwingungsvorgänge sind häufig in lebenden und nichtlebenden Systemen Beispiele: zirkadiane Rhythmen, Muskelkontraktionen im Herz, Puls, Anzahl der Individuen einer Population Uhrpendel, Rotation der Erde um die Sonne, Bewegung eines Motorkolbens T x Harmonische Schwingung x0 Sinusfunktion Weg-Zeit-Gesetz x = x0 sin ωt t Geschwindigkeits-Zeit-Gesetz v = ωx0 cos ωt v0 = ωx0 Beschleunigungs-Zeit-Gesetz a = - ω2x0 sin ωt a0 = ω2x0 - x0 T - Periodendauer ω = 2π T ω - Kreisfrequenz 5 Kräfte - Newtonsche Axiome sie verknüpfen die Kinematik und Dynamik eines Bewegungsvorganges Trägheitsprinzip Jeder Körper verharrt im Zustand der Ruhe oder der gleichförmigen geradlinigen Bewegung solange keine Kräfte auf ihm einwirken bzw. alle wirkenden Kräfte sich gegenseitig aufheben. Aktionsprinzip Ein frei beweglicher Körper mit der Masse m erfährt durch eine Kraft F eine Beschleunigung a, die der wirkenden Kraft proportional ist. F=ma Reaktionsprinzip Wirken zwei Körper a und b aufeinander ein und übt a auf b die Kraft Fab aus, so wirkt b auf a, so wirkt b auf a mit der entgegengesetzt gleichgroßen Kraft Fba = - Fab zurück. actio = reactio Schwerkraft sie wirkt auf jeden Körper auf der Erdoberfläche und ist zum Mittelpunkt der Erde gerichtet mk Fs = mk g Schwerkraft mk – Masse des Körpers Fs g – Fallbeschleunigung [F] = kg m s-2 g = 9,81 m s-2 Isaac Newton (1643 – 1727) 1 kg m s-2 = 1 N mk = ρk V ρk – Dichte des Körpers V – Volumen Fs = ρ k V g 6 Auftrieb der Auftrieb wirkt der Schwerkraft entgegen und hängt von der Masse des vom Körper verdrängten Mediums ab Prinzip von Archimedes Ein in eine Flüssigkeit eingetauchter Körper erfährt einen scheinbaren Gewichtsverlust, der gleich dem Gewicht der von Körper verdrängten Flüssigkeitsmenge ist. Ein Körper verdrängt eine bestimmte Menge an Medium (Luft, Wasser usw.) der Masse mm Auftrieb FA = mm g FA mk, V F A = ρm V g ρm – Dichte des Mediums Fs Auftrieb die Dichten von Körper und Medium bestimmen das (Bewegungs)verhalten des Körpers Werte für die Dichte: FA = ρm V g Luft 1,027 kg m-3 Wasser 1000 kg m-3 Eis Holz Fs = ρk V g 917 kg m-3 400-800 kg m-3 Eisen 7000 kg m-3 Kupfer 8933 kg m-3 Fallbetrachtung: 1) ρk > ρm → Fs > FA Körper sinkt Der Auftrieb im Medium Luft kann in der Regel vernachlässigt werden. 2) ρk = ρm → Fs = FA Körper schwebt 3) ρk < ρm → Fs < FA Körper steigt auf 7 Reibung zwischen Festkörpern Haft-, Gleit- oder Rollreibung müssen überwunden werden, damit sich der Körper bewegt bzw. seine Bewegungszustand aufrecht erhalten wird zwischen nicht bewegten Körpern Haftreibung FR,H = µH N Haftreibung FR,H F µH – Haftreibungskoeffizient hängt ab von Material und Oberflächenbeschaffenheit von Körper und Unterlage F N Fs Fs N – senkrecht auf die Unterlage wirkende Komponente der Schwerkraft F < FR,H Körper haftet F = FR,H Körper beginnt zu gleiten Gleitreibung, Rollreibung zur Aufrechterhaltung des Gleitens bzw. Rollens muss auch eine Reibung überwunden werden FR,G = µG N Gleitreibung FR,R = µR N Rollreibung µH > µG >> µR µG, µR – Gleit- bzw. Rollreibungskoeffizient Reibung in Flüssigkeiten in Flüssigkeiten hemmt die Reibung zwischen Flüssigkeitsschichten die Bewegung eines Körpers Körper bewegt sich relativ zum Medium das Medium hemmt die Bewegung FR FA → Reibungskraft FR Die Reibungskraft ist immer der Bewegung entgegen gerichtet! Flüssigkeit Fs Fs > FA Körper sinkt Reibung erfolgt zwischen den einzelnen Flüssigkeitsschichten Innere Reibung v Eine dünne Flüssigkeitsschicht haftet am Körper und bewegt sich wie der Körper. analoge Aussagen gelten für die Reibung in Gasen 8 Reibung in Flüssigkeiten die Viskosität von Flüssigkeiten beeinflusst das Reibungsverhalten Fs = ρk V g FR F A = ρm V g FA Reibungskoeffizient nach Stokes für kugelförmige Körper mit dem Radius rk FR ~ v FR = 6 π η rk v Flüssigkeit Reibungskraft η - Viskosität (Zähigkeit, innere Reibung) Fs [η] = Ns m2 = Pa s Werte für die Viskosität: Fs > FA Körper sinkt Wasser, 0ºC: Wasser, 20ºC: Wasser, 80ºC: Blut: Blutplasma Rizinusöl, 20ºC: 1,792x10-3 Pas 1,002x10-3 Pas 0,355x10-3 Pas 3-4x10-3 Pas 1,6-2,2x10-3 Pas 990x10-3 Pas Sedimentation hier stellt sich nach einer kurzen Anfangsphase ein Kräftegleichgewicht ein Fs = ρk V g FR F A = ρm V g FA V = 4 πr 3 k 3 FR = 6 π η rk v Fs - FA - FR = 0 Flüssigkeit Bestimmung der Viskosität von Flüssigkeiten Fs η= 2 rk2 9v (ρk - ρm) g Weitere Anwendungen Fs > FA Körper sinkt Blutsenkung (Zellaggregate sedimentieren schneller als Einzelzellen) Trennung unterschiedlich großer Partikel Bestimmung von v aber auch Flotation (wenn ρk < ρm) 9 Kräfte bei Kreisbewegungen die über die Radialbeschleunigung verknüpfte Zentripetalkraft zwingt den Körper auf eine Kreisbahn ar = ω2r v FP = m ω2r ar M Zentripetalkraft m FP Die Zentripetalkraft zwingt den Körper auf eine Kreisbahn. Beispiele: Gravitation (Bewegung von Himmelskörpern) Gravitationskraft Elektrostatische Anziehung (Bohr‘sche Atommodell) Coulombsche Kraft (anziehend) Elastische Kräfte (Körper an einem Seil) Elastische Kraft Kräfte bei Kreisbewegungen die Zentrifugalkraft ist der Zentripetalkraft entgegen gerichtet FP = m ω2r bei alleiniger Wirkung von Fp würde sich der Körper der Kreismitte immer mehr nähern v ar M FP m FZ FZ = - FP Zentrifugalkraft Fliehkraft Die Zentrifugalkraft ist eine Trägheitskraft. Am Körper der Masse m greift eine Kraft FZ an, die sich der aufgezwungenen Kreisbewegung widersetzt. 10 Zentrifugation mittels Zentrifugation werden zelluläre und subzelluläre Proben getrennt Winkelbecherrotoren M r Schwenkbecherrotoren FZ = mk ω2r FR FA = mM ω2r FR = 6 π η rk v FZ r FA FZ = F A + FR (für ρk > ρM) v = const Zentrifugation die Sedimentationskonstante charakterisiert Makromolekülen bei Sedimentation (für ρk > ρM) v Beispiele Insulin r Berechnung von v FA = mM ω2r FZ = FA + FR v = S S= 2 rk2 9η FZ = mk ω2r FR = 6 π η rk v m=ρV 4 V = π r k3 3 ( ρk - ρM) ω2r Svedberg Sedimentationskonstante v ω2r [S] = s Sk in S Mol.-gew. in Da 1,2 6 300 Myoglobin 2,0 16 900 Hämoglobin 4,5 63 000 Fibrinogen 7,6 340 000 Ribosom 70 1 000 000 Tabakmosaikvirus 174 (Protein) 59 000 000 die Sedimentationskonstante hängt nur von Eigenschaften des Teilchens und Mediums ab sie widerspiegelt die Größe eines Biomoleküls 1 S = 10-13 s 11 Kräftegleichgewichte Schweben bzw. Schwimmen Sedimentation FA FA Fs Fs FR FA Fs Fs = F A Zentrifugation Bewegungen auf einer Kreisbahn FR FP = FZ FP FS = F A + FR FZ FZ FA FZ = FA + FR Arbeit bei Kraftwirkung wird an einem Körper Arbeit verrichtet F α Spezielle Formen der Arbeit s Hubarbeit h W = mgh W = F s cosα [ W ] = Nm Arbeit Joule 1 Nm = 1 J m Beschleunigungsarbeit m allgemeiner W= 1 2 mv2 v=0 v W = ∫ Fds Arbeit ist eine skalare Größe 12 Energie und Leistung Energie und Leistung sind skalare Größen Energie - Fähigkeit eines Körpers Arbeit zu verrichten Potenzielle Energie Energie der „Lage“ in zeitlich konstanten Kraftfeldern Beispiel: angehobener Körper Kinetische Energie Energie der Bewegung Leistung verrichtete Arbeit P = W t Watt [P]=W 1 W = 1 J s-1 = 1 Nms-1 Energieerhaltungssatz der Mechanik das ist ein Sonderfall des allgemeinen Energieerhaltungssatzes In einem abgeschlossenen System bleibt die Gesamtenergie, das heißt die Summe aus potenzieller und kinetischer Energie, konstant. Epot + Ekin = const Spezialfall des allgemeinen Energieerhaltungssatz In jedem abgeschlossenen System bleibt die Gesamtenergie konstant. Energie kann weder erzeugt noch vernichtet werden; sie kann nur von einer Form in eine andere umgewandelt werden. Andere Energieformen: Wärmeenergie, elektrische Energie, chemische Energieformen, Bindungsenergie, Strahlungsenergie usw. 13 Impuls auch der Impuls ist eine Erhaltungsgröße Impulserhaltungssatz p=mv In einem abgeschlossenen System (es wirken keine äußeren Kräfte) bleibt der Impuls erhalten. Impuls Beispiel 1: Rückstoß [ p ] = kg m s-1 F= a= mR v=0 ∆v ∆t vG ∆t ∆p mG p=0 p=0 ∆(m v) F= unmittelbar nach dem Start m Aktionsprinzip F=ma vR vor dem Start p = mRvR + mGvG Beispiel 2: Entarretierung einer Feder ∆t danach zuvor v1 F ∆t - Kraftstoß m1 v1 = 0 m2 v2 = 0 v2 m1 p=0 m2 p=0 p = m1v1 + m2v2 Elastischer und inelastischer Stoß in beiden Fällen gelten Impuls- und Energieerhaltungssatz gleichzeitig Inelastischer Stoß Elastischer Stoß Teilchen werden nicht bleibend verformt Plastische Verformungen an den stoßenden Körpern Energieerhaltungssatz der Mechanik gilt Es gilt der allgemeine Energieerhaltungssatz, aber nicht der Energiesatz der Mechanik Beispiel: Frontalzusammenstoß zweier Kraftfahrzeuge Beispiel: Zentraler Stoß zweier Billardkugeln zuvor danach (´) v1 m1 2 v1 v2 m1 m2 m2 m1v1 = m1v1´ + m2v2´ 1 zuvor m1v12 = 1 2 m1v1´2 + 1 2 m1 danach v2 v´ m2 m1 + m2 m1v1 – m2v2 = (m1 + m2)v´ m2v2´2 v1´ = 0 v2´ = v1 (m1 = m2) 14 Drehmoment ist eine der Kraft analoge Größe bei Rotationsbewegungen Drehachse (senkrecht zur Tafelebene) α‘ F⊥ F α r M = F r sinα [ M ] = Nm mit F⊥ = F sinα‘ M = F⊥ r α‘ r⊥ Drehmoment und sinα‘ = sinα mit r⊥ = r sinα‘ M = F r⊥ und sinα‘ = sinα Gleichgewicht Σ Fi = 0 M = F r i das Drehmoment ist ein axialer Vektor durch ein Drehmoment ändert der Körper seine Winkelgeschwindigkeit ω, er erfährt somit eine Winkelbeschleunigung α und Σ Mi = 0 i d. h. es tritt keine Translations- und Rotationsbeschleunigung auf Kräftegleichgewichte Drehmomentengleichgewichte Trägheitsmoment, Rotationsbewegungen durch ein Drehmoment wird die Winkelgeschwindigkeit eines Körpers geändert Drehachse (senkrecht zur Tafelebene) F r M = Fr m v=ωr F=ma F=m ∆v ∆t F=mr Aktionsprinzip für Rotationsbewegungen M=θα Kinetische Energie für Rotationsbewegungen ∆ω ∆t Ekin = 1 2 θω2 M = m r2 α θ = m r2 Trägheitsmoment [ θ ] = kg m2 15 Drehimpuls für den Drehimpuls gilt ebenfalls ein Erhaltungssatz Drehimpulserhaltungssatz L = θω Drehimpuls Wirken auf ein System keine äußeren Drehmomente, so bleibt der Gesamtdrehimpuls des Systems konstant [ L ] = kg m2 s-1 Beispiel: Pirouette L ω v r Drehimpuls und Winkelgeschwindigkeit sind axiale Vektoren θ1 ω1 = θ1 > θ2 θ2 ω2 ω1 < ω2 Zusammenfassung Translation Rotation Weg s Winkel ϕ Geschwindigkeit v Winkelgeschwindigkeit ω Beschleunigung a Winkelbeschleunigung α Radialbeschleunigung ar Masse m Trägheitsmoment θ Kraft F Drehmoment M M=θα F=ma Kin. Energie Impuls 1 mv2 2 p Kin. Energie Drehimpuls 1 θ ω2 2 L 16 Elastische Eigenschaften, Deformation fester Körper Körper können unter Kraftwirkung auch deformiert werden Wirkungen von Kräften Beschleunigung von Körpern, Ortsveränderung Veränderung der Körperform, Deformation Elastische Deformation Plastische Deformation Der Körper nimmt nach Wegfall der wirkenden Kraft seine ursprüngliche Form wieder an in der Regel bei „kleinen“ Kräften Formveränderung bleibt dauerhaft bestehen Kräfte überschreiten bestimmte Schwellenwerte Materialbruch bei stärkeren Belastungen Feder als elastisches Element mit einer elastischen Feder können Kräfte gemessen werden Elastische Kraft auch Federkraft genannt Rückstellkraft einer Feder bei Dehnung (actio = reactio) Fel = D s gilt für kleine Kräfte Fel – elastische Kraft, Federkraft D - Federkonstante s [D]=N/m Beispiele: Federwaage, Gummiseil Fel m Fs Spannarbeit W= 1 2 Fel Ds2 s 17 Dehnung Körper werden durch Zugkräfte gedehnt A F l Kraft greift senkrecht an der Stirnfläche des Stabes an → Zugkraft l ε = ∆l σ = l ε - Dehnung Der Stab wird durch die Kraft F um die Strecke ∆l gedehnt F ∆l F σ ∼ ε A σ - Zugspannung Hookesches Gesetz Hookesches Gesetz es gilt nur bei Proportionalität von Zugspannung und Dehnung Spannungs-Dehnungs-Diagramm σ = Eε σ E - Elastizitätsmodul Pascal [ E ] = N / m2 = Pa der Elastizitätsmodul ist eine materialspezifische Größe und beschreibt eine elastische Eigenschaft von Materialien Beispiele für E ε Kupfer 1,2 ∗ 1011 Pa Knochen 1010 Pa Kautschuk 106 Pa 18 Querkontraktion Zugkräfte verändern auch die Querabmessung von Körpern l F ∆l ∆a/2 l εQ = F ∆l ∆a Verringerung der Querabmessung (Durchmesser, Kantenlänge) εQ = - µ ε a µ: 0 ... 0,5 Knochen: Kupfer: Kautschuk: µ - Poissonsche Zahl εQ - Querkontraktion 0 0,35 0,5 materialspezifische Größe Dehnung und Stauchung Stauchung ist das Gegenstück zur Dehnung Dehnung ∆a/2 l ∆l F Verlängerung Querkontraktion Volumenzunahme Stauchung ∆a/2 F l Verkürzung Querdilatation Volumenabnahme ∆l 19 Allseitige Kompression hier wird der Körper allseitig gleichmäßig belastet F σ = F F F Druckspannung A Volumenverminderung eines Körpers bei erhöhtem Druck Form bleibt dabei erhalten F σ = K F ∆V ∆V V V K - Kompressionsmodul = 3 (1 - 2 µ) ε K= E 3(1 - 2µ) relative Volumenänderung entspricht Stauchung in allen drei Raumrichtungen [ K ] = Pa materialspezifische Größe Scherung bei dieser elastischen Verformung wird der Körper seitlich versetzt A Kraft greift tangential zur Auflagefläche an → Schubkraft F Scherwinkel β τ = F Schubspannung A F G – Schermodul τ = Gβ [ G ] = Pa materialspezifische Größe Scherung und Dehnung treten meist gleichzeitig auf G = E 2(1 + µ) 20 Arten der elastischen Verformung Dehnung Verdrillung (Torsion) Biegung F F F F Stauchung Scherung F Allseitige Kompression F F Materialspezifische Größen F F F F Elastizitätsmodul E Poissonsche Zahl µ Kompressionsmodul K Schermodul G Plastisches Verhalten hier wird der Körper irreversibel deformiert Spannungs-Dehnungs-Diagramm σ Elastizitätsgrenze bei Überschreiten der Elastizitätsgrenze wird der Körper irreversibel deformiert → plastische Deformation Fließgrenze Bruchgrenze Proportionalitätsgrenze Kurvenverlauf nach Überdehnung ε εpl bei vollständiger Entlastung bleibt dauernde Dehnung zurück bei erneuter Belastung σ(ε) auf der gestrichelten Kurve bei Überschreiten der Fließgrenze beginnt das Material bei starker Verkleinerung des Querschnitts zu fließen → Materialbruch an der Bruchgrenze plastische Materialien weisen einen breiten Bereich der plastischen Deformation auf (sie sind verformbar, z. B. Metalle) spröde Materialien haben einen sehr engen Bereich der plastischen Deformation (z. B. Glas, Porzellan) 21 Zeitverhalten bei Deformationen Materialien zeigen bei Belastung ein unterschiedliches Zeitverhalten Elastisches Verhalten F Visköses Verhalten F Viskoelastisches Verhalten F t t ∆l ∆l t ∆l t t Formänderung folgt unmittelbar der Kraftänderung allmähliche Formänderung veränderte Form bleibt erhalten Beispiel: Schraubenfeder Kolben in zäher Flüssigkeit t zeitverzögerte Antwort auf Kraftwirkung Parallelität von Feder und Kolben Bedeutung des viskoelastischen Verhaltens wichtige Elemente des Bewegungsapparates reagieren zeitverzögert ∆l F zeitverzögerte Einstellung neuer Zustände Kraftstoß Relaxationserscheinungen Abpufferung von Kraftstößen bei heftigen Bewegungen (Sprünge, Würfe u.a.) t Umorientierung und Ausrichtung polymerer Makromoleküle Wassereinlagerung Viskoelastische Elemente Gelenkknorpel Sehnen Bänder 22 Druck der Druck ist eine wichtige Eigenschaft in Flüssigkeiten und Gasen In Gasen und Flüssigkeiten sind die einzelnen Teilchen in ständiger Bewegung Druck offenbart sich an Gefäßwänden oder Hindernissen v⊥ → „Trommelfeuer“ F = m m, v v= F dv dt v⊥ - v⊥ v= bleibt F p = A p - Druck A - Querschnittsfläche [ p ] = N / m2 = Pa (Pascal) Luftdruck die umgebende Luft übt einen definierten Druck aus p0 = 101,3 kPa = = = = 1 atm 1,013 bar 760 Torr 760 mmHg p = p0 e der Luftdruck nimmt mit zunehmender Höhe ab p p0 - (ρ0 / p0) gh p0/2 Barometrische Höhenformel p0 ρ0 g e - Druck bei h = 0 Dichte bei h = 0 9,81 m / s2 2,718 0 h1/2 Meeresspiegel h ~ 5500 m 23 Schweredruck er tritt in Flüssigkeiten auf und hängt von der Höhe der Flüssigkeitssäule ab Druck in Flüssigkeit hängt von Höhe der darüber liegenden Flüssigkeitssäule ab h p = ρgh Der Schweredruck hängt nicht von der Gefäßform ab Schweredruck ρ - Dichte g - Fallbeschleunigung h - Höhe der Flüssigkeitssäule Der Schweredruck ist eine Druckkomponente, die zusätzlich zum äußeren Druck wirkt Stempeldruck er tritt in Flüssigkeiten und Gasen auf, die sich in einem geschlossenen Gefäß befinden A p = F F A Stempeldruck Flüssigkeit strömt aus Druckkomponente, die zusätzlich zum äußeren Druck wirkt (analog Schweredruck) Schweredruck und Stempeldruck können gleichzeitig auftreten Beispiele: Kolben, Spritzen, Pumpen, Herz 24 Blutkreislauf das Herz erzeugt einen Stempeldruck und pumpt Blut in den Körper- und Lungenkreislauf Herzminutenvolumen 4 – 5 l/min Volumen an Blut pro Herzschlag rund 70 ml Anzahl der Herzschläge pro Zeit 60 – 70 min-1 linke Herzkammer Systole 120 mmHg (16 kPa) Diastole ~ 0 mmHg Oberarm 120 mmHg (16 kPa) 80 mmHg (10.7 kPa) Strömende Flüssigkeiten, Grundbegriffe Druckdifferenz und Stromstärke sind wichtige Kenngrößen in der Hämodynamik l Ursache für eine Strömung: Druckdifferenz längst einer Strecke ∆p = p1 - p2 p1 > p2 ∆V p1 p2 ∆p Druckgradient l I = ∆V hydrodynamische Stromstärke ∆t I ~ ∆p I = [I] = m3 s Maß für die Menge, die strömt 1 RH ∆p RH - Strömungswiderstand Grundgesetz der Hämodynamik (in Analogie zum Ohmschen Gesetz in der Elektrik) 25 Kontinuitätsgleichung diese Gleichung resultiert aus der Inkompressibilität von Flüssigkeiten v1 l A ∆x p1 ∆V I = ∆t v2 ∆V p2 I = A A2 A1 Flüssigkeiten sind inkompressibel ∆x ∆t I1 = I2 v I = Av A1 v1 = A2 v2 Kontinuitätgleichung v - mittlere Strömungsgeschwindigkeit Strömungsarten eine laminare Strömung ist energetisch günstiger Strömung in Schichten Stromlinien verlaufen parallel, sie überschneiden sich nicht v=0 am Rand vmax in der Mitte parabolische Verteilung der Geschwindigkeit infolge der inneren Reibung laminare Strömung Bildung von Wirbeln Stromlinien nicht parallel, sie überschneiden sich Bei Zunahme der Strömungsgeschwindigkeit schlägt ein laminarer Fluss in eine turbulente Strömung um. Blutgefäße: in der Regel laminare Strömung energetisch ungünstiger turbulente Strömung bei Turbulenzen: hohe v an Gefäßwänden → Gefahr einer Endothelschädigung 26 Strömungswiderstand bei laminarem Fluss der Gefäßradius bestimmt wesentlich die Stromstärke l Regulation der Durchblutung I ~ r4 p1 I ~ p2 ∆ p I = π r4 I = ∆ 8ηl p ∆ kleine Änderungen des Gefäßtonus führen zu großen Änderungen der Stromstärke p RH Hagen-Poiseuillesches Gesetz Newton‘sche Flüssigkeit I η = const RH = 8ηl Strömungswiderstand π r4 ∆p Parallel- und Reihenschaltung von Gefäßen analoge Betrachtungen gelten für elektrische Ströme Verzweigung von Gefäßen I1 I I2 l ∆p1 RH1 ∆p2 RH2 I = I1 + I2 in jedem Verzweigungspunkt ist die Summe der einlaufenden Ströme gleich der Summe der abfließenden Ströme ∆p1 = ∆p2 in parallelen Strömungszweigen herrscht dasselbe Druckgefälle 1 RH, ges = 1 RH1 + 1 RH2 Hintereinanderschalten von Gefäßen I1 RH1 ∆p1 I2 RH2 ∆p2 I = I1 = I2 RH, ges = RH1 + RH2 ∆p1 = I RH1 ∆p2 = I RH2 27 Statischer Druck der statische Druck vermindert sich in bewegten Medien Druck als Trommelfeuer Ruhendes Medium Komponentenzerlegung des Geschwindigkeit v p=F/A Der senkrecht auf eine Fläche wirkende Druck heißt statischer Druck F Bewegtes Medium flacherer Aufprall der Teilchen auf Wand in bewegten Medien v die wirkende Kraft F und somit der statische Druck p werden kleiner je größer v, desto kleiner p F Gleichung von Bernoulli diese Gleichung folgt aus dem Energieerhaltungssatz v1 V v1 < v2 Annahmen: v2 kein Druckabfall zwischen 1 und 2 V reibungsfreie Strömung (µ = 0) starres Gefäß A2 „ideale Flüssigkeit“ „ideale Strömung“ A1 v1 < v2 Wpot + Wkin m p1 V + v2 2 1 p1 + ρ 2 p+ = m p2 V + v2 2 2 v12 = p2 + ρ 2 ρ 2 v2 = const / :V v22 ρ 2 p1 > p2 an der engeren Stelle wird der kleinere Druck gemessen p - hydrostatische Druck (wirkt senkrecht auf die Gefäßwand) v2 - Staudruck, dynamische Druck 28 Phänomene an Mediengrenzen zahlreiche Interaktionen zwischen Molekülen finden in biologischen Systemen an Mediengrenzen statt Mediengrenzen: fest / fest fest / flüssig fest / gasförmig flüssig / gasförmig flüssig / flüssig (nicht mischbare Flüssigkeiten) Festkörper: definiertes Volumen, definierte Form Flüssigkeit: definiertes Volumen, Form passt sich an Gas: füllt einen zur Verfügung stehenden Raum aus Mediengrenzen sind gleichzeitig Kontaktflächen Form von Mediengrenzen (und damit die Ausbildung von Strukturen) wird durch Wechselwirkungen der beteiligten Moleküle bestimmt → Energieminimum Wechselwirkungskräfte benachbarte Moleküle interagieren miteinander Medium 1 Kohäsionskräfte Kräfte zwischen Molekülen eines Mediums Medium 2 Adhäsionskräfte Kräfte zwischen Molekülen unterschiedlicher Medien Fallbetrachtung Fkoh > Fadh kleine Kontaktfläche, Tropfenbildung nicht benetzende Flüssigkeiten Fkoh < Fadh große Kontaktfläche, benetzende Flüssigkeiten 29 Oberflächenspannung diese Größe verknüpft Änderungen der Energie und Oberfläche miteinander σ ist eine spezifische Größe Beispiele: Oberfläche A nimmt ab bei gleichbleibendem Volumen Energie wird frei ∆W = σ ∆A 72,9 • 10-3 N/m 50 • 10-3 N/m Quecksilber 478 • 10-3 N/m 32 • 10-3 N/m Oberflächenspannung eines der Medien ist Luft ∆A - Änderung der Oberfläche σ Wasser Blutplasma Olivenöl ∆W - freigesetzte bzw. benötigte Energie Luft / Medium Grenzflächenspannung zwei beliebige Medien - Oberflächenspannung [ σ ] = J / m2 = N / m Abreißen einer Flüssigkeitslamelle, Drahtbügel l l x x ∆x F ∆W = F ∆x ∆W = σ 2 l ∆x F F F F = 2σl Mit der Drahtbügelmethode kann die Oberflächenspannung von Flüssigkeiten bestimmt werden 30 Abreißen einer Flüssigkeitslamelle, Metallring ∆W σ = F ∆A Metallring Fmax h ∆W = Kraft im Moment des Abreißens Flüssigkeitsfilm d h ∆A = 2 π d h σ = Fmax 2πd Auch mit einem Metallring kann die Oberflächenspannung von Flüssigkeiten bestimmt werden Druck an gekrümmten Oberflächen im Inneren von Tropfen und Vesikeln herrscht ein höherer Druck als in der Umgebung Beispiel: p0 r p0 + ∆ p Wassertropfen oder Luftblase in Wasser ra ri ∆p = 2σ r σ = 72 • 10-3 N/m r = 10-3 m ∆p = 144 Pa r = 10-6 m ∆p = 144 kPa ∆p - Kohäsionsdruck ri ~ ra r ∆p = 4σ r Lamelle, Seifenblase Membranvesikel 31 Oberflächenspannung und Tropfengröße auch die Größe von Tropfen hängt von der Oberflächenspannung ab Bestimmung von σ über die Tropfengröße Tropfenzähler ra ∆A = 2π ra ∆x ∆W = Fs ∆x ri ∆W = σ ∆A Fs = 2π ra σ Fs ∼ σ Tropfengewicht und Oberflächenspannung sind proportional ∆x Vergleich mit Eichflüssigkeit (Wasser) σ1 = σ0 ρ1 · n0 ρ0 · n1 ρ - Dichten n - Tropfenzahl für ein gegebenes V Stalagmometer Fs Normaltropfenzähler Fs Effekte an Kapillaren Flüssigkeiten in enge Kapillaren zeigen ausgeprägte Oberflächeneffekte Benetzende Flüssigkeit Aszension möglichst große gemeinsame Oberfläche zwischen Flüssigkeit und Kapillare je enger die Kapillare, desto ausgeprägter der Effekt Beispiele feuchtes Mauerwerk schlechte Isolation Aufstieg von Wasser in Pflanzen Depression Nichtbenetzende Flüssigkeit möglichst kleine gemeinsame Oberfläche zwischen Flüssigkeit und Kapillare 32 Effekte an Kapillaren die kapillare Steighöhe ist eine Funktion der Oberflächenspannung Fσ 2r rk Aszension Fs h ϕ Randwinkel kapillare Steighöhe Fs = ρFl πr2h g ps = ρFl h g p= ps = pσ 2σ rk h= 2σ r = cos ϕ bei vollständig benetzender Flüssigkeit (cos ϕ = 1) h= 2σ cos ϕ r ρFl g 2σ r ρFl g Oberflächenaktive Stoffe solche Stoffe akkumulieren an der Grenzfläche Wasser/Luft Luft vermindern z.T. drastisch σ (Wasser/Luft) lagern sich bevorzugt an der Grenzfläche an Wasser amphiphile Moleküle hydrophil Fettsäuren Seifen Tenside Phospholipide Cholesterol -O O hydrophob Beispiel: Palmitinsäure C die Strukturbildung in biologischen Systemen wird durch amphiphile Stoffe gewährleistet 33 Ausgewählte Wirkungen oberflächenaktiver Stoffe Verminderung der Oberflächenspannung in den Lungenalveolen durch Surfaktantien Bronchiole Luft Alveole Gewebe (Wasser) Grenzfläche Wasser / Luft σ = 72,9 x 10-3 N/m Surfaktantien (spezielle Phospholipide) bedecken die Innenseite der Alveolen σ etwa 1/10 von σWasser beim Atmen ändert sich die Oberfläche der Alveolen ständig elastische Verformung des Lungengewebe Wechselspiel zwischen Oberflächenenergie und elastischer Energie Surfaktantien minimieren den Energieaufwand bei der Atmung 34