Lernzielkatalog 6. Klasse

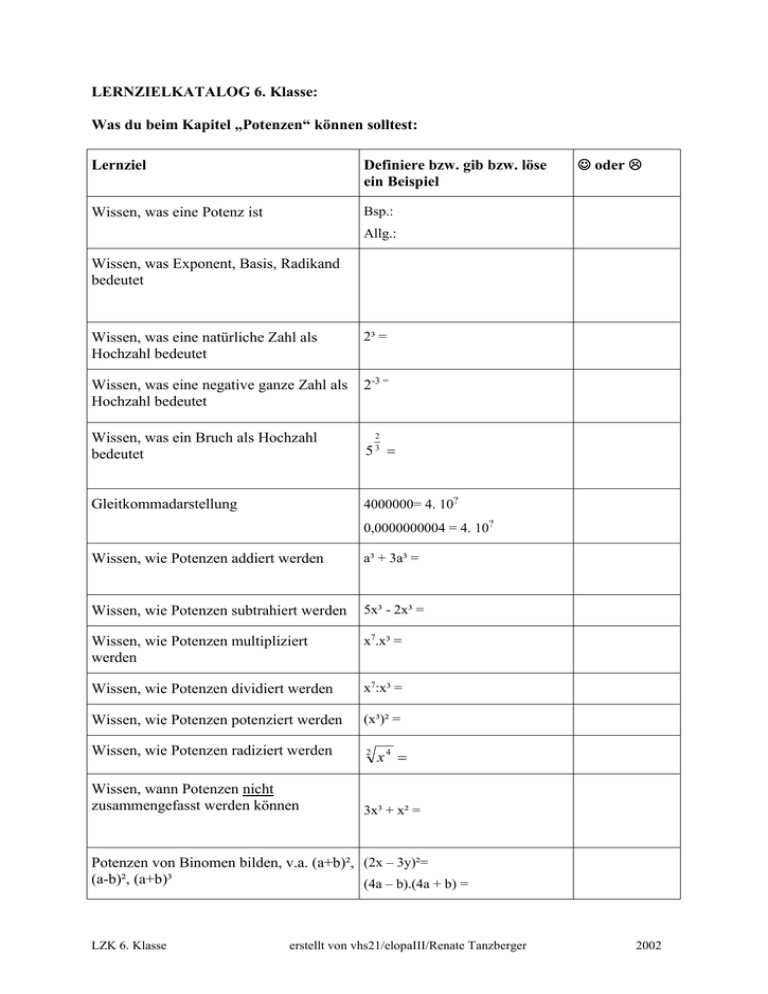
LERNZIELKATALOG 6. Klasse:
Was du beim Kapitel „Potenzen“ können solltest:
Lernziel
Definiere bzw. gib bzw. löse
ein Beispiel
Wissen, was eine Potenz ist
Bsp.:
 oder 
Allg.:
Wissen, was Exponent, Basis, Radikand
bedeutet
Wissen, was eine natürliche Zahl als
Hochzahl bedeutet
2³ =
Wissen, was eine negative ganze Zahl als
Hochzahl bedeutet
2-3 =
Wissen, was ein Bruch als Hochzahl
bedeutet
5 
Gleitkommadarstellung
4000000= 4. 10?
2
3
0,0000000004 = 4. 10?
Wissen, wie Potenzen addiert werden
a³ + 3a³ =
Wissen, wie Potenzen subtrahiert werden
5x³ - 2x³ =
Wissen, wie Potenzen multipliziert
werden
x7.x³ =
Wissen, wie Potenzen dividiert werden
x7:x³ =
Wissen, wie Potenzen potenziert werden
(x³)² =
Wissen, wie Potenzen radiziert werden
2
Wissen, wann Potenzen nicht
zusammengefasst werden können
x4 
3x³ + x² =
Potenzen von Binomen bilden, v.a. (a+b)², (2x – 3y)²=
(a-b)², (a+b)³
(4a – b).(4a + b) =
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Potenzen“ können solltest:
Binome zerlegen können
81x² - 18x + 1 =
16a² - 81b² =
32 
Partiell Wurzel ziehen
200 x ³ 
3
Nenner rational machen
81 
1

2
x y
x
Wurzelgleichungen lösen,
Definitionsgebiet bestimmen 
Ungleichungen lösen, Lösungsmenge
angeben
Potenzfunktion zeichnen, Nullstelle und
Fixpunkte bestimmen, Definitionsmenge
angeben, Monotonie angeben

y
2 x  11  2 x  5  8
4. x  20  3. x  6  7. x  2
1
8
f: y = - .x ³
Wurzelfunktion zeichnen, Nullstelle und
Fixpunkte bestimmen, Definitionsmenge
angeben, Monotonie angeben
f: y = 3.
Mit dem Taschenrechner umgehen
können (Tasten x², xy, x , n x ) und
richtig eingeben
Berechne mit dem TR:
x0=
0n=
x1=
(negative Zahl) gerade Zahl =
LZK 6. Klasse
x
2³ =
4
27 
n
n
x 
(negative Zahl) ungerade Zahl =
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Potenzen“ können solltest:
Kreuze an, welche Umformungen stimmen:
3a³ + 2a³ =
 5a³
 5a6
 kann nicht zusammengefasst werden
3a³ + 2a² =
 5a5
 5a6
 kann nicht zusammengefasst werden
3a³ . 2a³ =
 6a³
 6a6
 6a9
(3a³)2 =
 3a6
 9a6
 3a9
30 =
0
1
3
4
0 =
0
1
4
21 =
1
2

2-3 =

 -6
8
1
8
1
2
Gib bei den folgenden Beispielen an, ob sie richtig gelöst wurden bzw. – wenn nicht – wo
der Fehler liegt:
(-2)4 = -24
 stimmt
 stimmt nicht, es gehört _______________
-24 = -16
 stimmt
 stimmt nicht, es gehört _______________
(-2)³ = -8
 stimmt
 stimmt nicht, es gehört _______________
(3a + b)² = 9a² + b²
 stimmt
 stimmt nicht, es gehört _______________
(3.a.b²)³ = 27.a³.b6
 stimmt
 stimmt nicht, es gehört _______________
3 1
 stimmt
 stimmt nicht, es gehört _______________
3²  3
 stimmt
 stimmt nicht, es gehört _______________
 stimmt
 stimmt nicht, es gehört _______________
 stimmt
 stimmt nicht, es gehört _______________
 stimmt
 stimmt nicht, es gehört _______________
x 6  x²
 stimmt
 stimmt nicht, es gehört _______________
a²  1
 1
a²  1
 stimmt
 stimmt nicht, es gehört _______________
 stimmt
 stimmt nicht, es gehört _______________
3
3x²y² = (3xy)²
3.x-3 =
1
3x³
3
5 2  3 5²
3
200  10. 2
(9x² - 6x +1) = (3x-1)²  stimmt
 stimmt nicht, es gehört _______________
16x4y² - 4x²y4 = 4x²y²(4x² - 1) = 4x²y².(2x + 1) . (2x – 1)
2
 
3
1
2
2


32
2
2
2
LZK 6. Klasse
 stimmt
 stimmt nicht
 stimmt
 stimmt nicht, es gehört _______________
 stimmt
 stimmt nicht, es gehört _______________
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Grenzprozesse“ können solltest:
 oder 
Lernziel
Definition Folge (im
Unterschied zu Menge)
Gib jeweils ein Beispiel:
Festlegen von Folgen durch
Rekursion und einen
erzeugenden Term
Gib jeweils die ersten fünf Glieder der Folge an:
a) 2n-1 
b) x1 = 1
Arithmetische Folgen:
- Wie definiert?
xn+1 = xn.2
Gib ein Beispiel für eine arith. Folge und
berechne die ersten 5 Folgenglieder:
- Wie wird das n-te
Folgenglied berechnet?
Geometrische Folgen:
- Wie definiert?
Gib ein Beispiel für eine geometr. Folge und
berechne die ersten 5 Folgenglieder:
- Wie wird das n-te
Folgenglied berechnet?
Was ist das arithmetisches
Mittel?
Gib das arithmetische Mittel von 12 und 36 an:
Was ist das geometrisches
Mittel?
Gib das geometische Mittel von 25 und 81 an:
Monotonie von Folgen:
Beweise, dass die Folge <
Formale Definition für
- streng. monoton wachsend
2  4n
> streng
8n  5
monoton fallend ist!
- streng monoton fallend
Monotonie bei Folgen
nachweisen können
Schranken von Folgen:
Formale Definition für
- untere Schranke
2  4n
> durch –1 nach
8n  5
unten und durch 0 nach oben beschränkt ist.
Beweise, dass die Folge <
- obere Schranke
Schranken von Folgen
nachweisen können.
Feststellen können, ob eine
Folge beschränkt ist.
Was sind konvergente
Folgen?
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Grenzprozesse“ können solltest:
Was sind divergente Folgen?
Grenzwert:
Bestimme den Grenzwert a der Folge <
- Wie ist der Grenzwert
einer Folge definiert?
2  4n
>
8n  5
- Wie kann der Grenzwert
einer Folge nachgewiesen
werden?
- Die Grenzwertesätze zum
Berechnen von Grenzwerten anwenden können.
Endliche arithmetische Reihe: <3, 5, 7, 9,...> Gib die ersten 5 Glieder der
zugehörigen Reihe an und berechne das 10.
- Definition
Reihenglied!
- Das n-te Glied berechnen
können.
Endliche geometrische Reihe: <12, 6, 3,...> Gib die ersten 5 Glieder der
zugehörigen Reihe an und berechne das 10.
- Definition
Reihenglied!
- Das n-te Glied berechnen
können.
- Textaufgaben lösen
können
Unendliche geometrische
Reihe:
a) Hat die zu <12, 6, 3,...> gehörende Reihe eine
Summe? Wenn ja, berechne sie.
- Definition
- Die Summe (so
vorhanden) berechnen
können.
- Wann kann die Summe
gar nicht berechnet
werden?
- Textaufgaben lösen
können
LZK 6. Klasse
b) An einem Halbkreis vom Radius r wird ein
Halbkreis von halb so großem Radius in umgekehrter Orientierung angesetzt. Setzt man dieses
Verfahren fort, so erhält man eine Folge von
Schlangenkurven. Berechne die Länge dieser
unendlichen Kurve (hat sie eine Länge?) und
die Flächeninhalte aller Halbkreise!
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Grenzprozesse“ können solltest:
TEST zu „Grenzprozesse“:
1. Gib an, ob eine arithmetische oder eine geometrische Folge vorliegt:
1, 4, 7, 10,...
27, 9, 3, 1,...
1, -2, 3, -4, 5,...
4, -8, 16, -32, 64,...
3, 1, -1, -3,...
2. Von einer arithmetischen Folge sind gegeben: a5 = 17/2, a11 = 41/2.
Berechne a1, d und s12!
3. Zwischen den Zahlen 6 und 96 sollen drei Zahlen so eingefügt werden, dass sie eine
geometrische Folge bilden. Wie lauten die einzufügenden Zahlen?
4. Gegeben sei die Folge <
3n  5
>
2  9n
a) Gib die ersten 5 Folgenglieder an!
b) Gib eine obere Schranke der Folge an und beweise sie.
c) Stelle eine Vermutung bzgl. der Monotonie der Folge auf und beweise diese!
d) Bestimme den Grenzwert a der Folge, beweise den Grenzwert und gib an, ab
welchem Folgenglied alle weiteren in einer -Umgebung mit = 1/200 um den
Grenzwert a liegen.
5. Einem Quadrat mit der Seitenlänge a wird ein Quadrat eingeschrieben, dessen
Eckpunkte die Seiten des ursprünglichen Quadrats im Verhältnis 5 : 12 teilen. Dem 2.
Quadrat wird nach der selben Vorschrift ein 3. Quadrat eingeschrieben, usw.
a) Berechne die Summe der ersten 10 Quadratumfänge!
b) Berechne die Summe aller Quadratflächen (wieso kannst du davon ausgehen,
dass diese unendliche Reihe überhaupt eine Summe hat?).
6. Welchen Grenzwert haben folgende Folgen:
2  n3
n2 + 1
5n  3
2n  1
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Exp. / Log.“ können solltest:
 oder 
Lernziel
Gib ein Beispiel für eine
Exponentialfunktion an!
Beispiel:
Weißt du, wie du diese Funktion
zeichnest?
Kannst du ein paar Eigenschaften
dieser Funktion angeben?
Gib die allg. Definition für die
Exponentialfunktion an:
Definition:
Wie lautet die eulersche Zahl?
Die eulersche Zahl ist der Grenzwert
welcher Folge?
Kannst du e³ mit dem Raschenrechner
berechnen?
Gib ein Beispiel einer
Exponentialgleichung mit gleichen
Basen und versch. Exponenten:
Wie wird diese Gleichung gelöst?
Gib ein Beispiel einer
Exponentialgleichung mit versch.
Basen und gleichen Exponenten:
Wie wird diese Gleichung gelöst?
Beispiel:
Lösung:
Beispiel:
Lösung:
Wie ist der Logarithmus definiert?
Kannst du mit Hilfe der Definition
einfache Berechnungen ohne TR
durchführen?
2
log 8 = x  x=
, da
4
log b = 3  b=
, da
a
log 5 = -1  a=
, da
a
log 1 =
, da
a
log a =
, da
Welche Basis hat der lg [im TR oft
mit log abgekürzt]?
Was ergibt daher lg1000?
Welche Basis hat der ln?
Was ergibt daher ln(1/e)?
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Exponentialfunktion, Logarithmus, -funktion“ können solltest:
 oder 
Lernziel
Kannst du den lg und ln mit Hilfe des z.B. lg25 =
TR berechnen?
z.B. ln0,2 =
Kennst du die Gesetzte für das
Rechnen mit Logarithmen?
a
log (uv) =
a
log
a
log un =
a
log
=
=
Kannst du komplexere Umformungen Beispiel: Zerlege den Term:
vornehmen?
log (a².b³) =
Beispiel: Verwandle in einen Term:
¼ . log(a² +b) – ½ . log c =
Welcher Zusammenhang besteht
zwischen alog x und blog x ?
Formel:
Berechne mit Hilfe der Formel und
des TR 3log 1,7
Gib ein Beispiel für eine
Logarithmusfunktion an!
Beispiel:
Weißt du, wie du diese Funktion
zeichnest?
Kannst du ein paar Eigenschaften
dieser Funktion angeben?
Gib die allg. Definition für die
Logarithmusfunktion an:
Definition:
Welcher Zusammenhang besteht
zwischen der Logarithmus- und der
Exponentialfunktion?
Kannst du Exponentialgleichungen,
die zu Logarithmusgleichungen
führen, lösen?
Kannst du Logarithmusgleichungen
lösen?
LZK 6. Klasse
Beispiel: 2x + 2x+1 = 3x-1
Beispiel: xlgx = 100x
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Exponentialfunktion, Logarithmus, -funktion“ können solltest:
TEST zu „Logarithmus, Exponentialfunktion“
1. a) Wie lautet die Umformung zu a log b = t ?
b) Berechne ohne Taschenrechner (mittels Umformung): lne2=
c) Berechne ohne Taschenrechner (mittels Umformung): lg0,1=
d) Berechne ohne Taschenrechner (mittels Umformung): 3log 81 =
e) Berechne die Basis: xlog9=-2
f) Berechne den Numerus: 3logx=2
2. Löse folgende Gleichungen:
a) 82x-5 = 26-x
Mache die Probe !!
b) lg(x+3) – lg(x-3) = lg4 Gib auch die Definitionsmenge an !!
c)72x+1 – 3.23x-1 = 9.23x-2 + 5.72x-1
3. Zeichen
f: y=2x-1
im Bereich von ]-3, 4] und
g: y = 1,5logx im Bereich von ]0, 7]!
4. Von mo Gramm Radium sind infolge radioaktiven Zerfalls t Jahre später nur mehr
m=m0.e-0,000428.t Gramm vorhanden.
a) Wie viel Gramm sind von m0=0,003g nach 100 Jahren noch vorhanden?
b) Wie groß war eine Radiummenge von derzeit 1,5.10-6 kg vor 1000 Jahren?
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Trigonometrie“ können solltest:
 oder 
Lernziel
Wie ist ein (Alt-)Grad definiert und
wie wird es unterteilt?
Kannst du mit den TR zwischen DMS 12° 5’ 12“ = _______°
und DD umrechnen?
16,375° = __° __’ __“
Wie ist der Radiant definiert?
1 rad =
Kannst du mit dem TR zwischen
Altgrad und Bogenmaß wechseln?
315° = ____ 
 = ____°
Mit Hilfe welcher zweier
geometrischer Figuren wurden die
Winkelfunktionen definiert?
1. ____________________
2. ____________________
Welche Winkelfunktionen kennst du? 1.
2.
3.
4.
Wie sind die Winkelfunktionen im
rechtwinkligen Dreieck definiert?
1.
2.
3.
4.
Wie sind die Winkelfunktionen im
Einheitskreis definiert?
Kannst du die Vorzeichen der
Winkelfunktionen in den 4
Quadranten des 1-Kreises angeben?
Mache eine Skizze und zeichne die
Winkelfunktionen für =75° und
=170° ein:
1.Qu. 2.Qu. 3.Qu. 4.Qu.
sin
cos
tan
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Trigonometrie“ können solltest:
Weißt du, wie du mit dem TR
Winkelfunktionen berechnen kannst?
[sowohl in Grad als auch in rad]
sin45°=
cos(2)=
tan315°=
Weißt du, wie du mit dem TR aus
einer gegebenen Winkelfunktion den
Winkel eruieren kannst?
Zu einem gegebenen Sinuswert gibt
es wie viele Winkel?
sin= 0,2  =
Zu einem gegebenen Cosinuswert gibt
cos= - 0,8  =
es wie viele Winkel?
Zu einem gegebenen Tangenswert
gibt es wie viele Winkel?
tan= 3,6  =
=
=
=
Wo ist der tan nicht definiert?
Wie sind die Polarkoordinaten
definiert?
Kannst du zwischen kartesischen und
Polarkoordinaten umrechnen? Worauf
musst du bei der Berechnung des
Winkels besonders achten?
a) P(-4/7)  r= _____
b) r=5, =195°
= ____
x=____ y=____
Was sagt der Sinussatz?
In welchem Dreieck darfst du ihn
anwenden?
Was musst du bei der Anwendung
beachten?
Was sagt der Cosinussatz?
In welchem Dreieck darfst du ihn
anwenden?
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Trigonometrie“ können solltest:
Weißt du, wo du nachschauen musst,
um die Formeln für die Dreiecksfläche und den Umkreisradius zu
finden?
Wenn ja, dann suche sie und schreibe
sie hier auf:
A=
r=
Weißt du, was Höhen-, Tiefen- und
Horizontalwinkel sind?
Höhenwinkel:
Tiefenwinkel:
Horizontalwinkel:
Weißt du, was Vertikal- und
Horizontalebenen sind?
Vertikalebenen:
Horizontalebenen:
Weißt du, wie du die Sinus-Funktion
zeichnest?
Kannst du ein paar Eigenschaften
dieser Funktion angeben?
Desgleichen mit der Cosinusfunktion!
Desgleichen mit der Tangensfunktion!
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Trigonometrie“ können solltest:
Test zu „Trigonometrie“:
1. a) Von einem Dreieck sind gegeben: a=21,6cm, b=13,3cm und =40° 54’
Mache eine Skizze, berechne c, ,  sowie den Umkreisradius und den Flächeninhalt.
b) Von einem rechtwinkligen Dreieck (=90°) mit dem gleichen Flächeninhalt ist a mit
14cm gegeben. Berechne b, c,  und .
2. Von der Spitze eines 62m hohen Turmes sieht man den Geländepunkt A unter einem
Tiefenwinkel von 24,22° und nach Schwenken des Fernrohres um einen Horizontalwinkel
von 76,38° den Geländepunkt B unter einem Tiefenwinkel von 29,93°.
Mache eine Skizze und ermittle die Entfernung von A nach B.
3. Ein Flugzeug fliegt auf geradlinigem Kurs mit der gleichbleibenden Geschwindigkeit von
540km/h über dem Boden und peilt im Abstand von 2 Minuten das selbe Funkfeuer an.
Die Winkel zwischen der Flugrichtung und dem Funkstrahl betrugen 14° bzw. 21°.
a) Welche Entfernung hatte das Flugzeug bei der 1. Peilung vom Funkfeuer, welche bei
der 2. Peilung?
b) In welcher Höhe passiert das Flugzeug das Funkfeuer?
4. Zeichne die Funktion f: y=4.cos(mit[0°,720°] und gib einen weiteren Hoch-,
Tiefpunkt und eine Nullstelle außerhalb des Definitionsgebietes an.
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Gleichungssysteme mit 3 Variablen“ können solltest:
 oder 
Lernziel
2 Gleichungen mit 3 Variablen lösen
können (+ geometrischer
Interpretation)
I 3x – 2y + z = 8
II 4x +3y - z = 7
3 Gleichungen mit 3 Variablen mittels I 2x + 5y + 4z = 1
II -3x – y – 2z = -10
Eliminationsverfahren oder
Cramer’scher Regel lösen können (+ III ½ x + 3y – 5z = 1,5
geometrischer Interpretation)
Wissen, welche Sonderfälle bei einem Zeige an Hand der Beispiele und gib
eine geometrische Interpretation:
3x3 Gleichungssystem auftreten
können und wie sich das auf die
I
2x – 3y + 4z = 17
Lösung auf wirkt?
II –6x + 9y – 12z = -51
III x – 1,5 y + 2z = 8,5
I
x + 2y + z = 12
II –x + y + z = 5
III z = 9x + 3y – 23
I
2x – 3y + 4z = 17
II –6x + 9y – 12z = 51
III x – 1,5 y + 2z = 8,5
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „Vektorrechnung“ können solltest:
 oder 
Lernziel
die Ebenengleichung in Parameter
und Normalvektorform angeben
können
Bestimme die Ebene, in der A(-1/0/2),
B(-3/0/4), C(2/2/2) liegen
das vektorielle Produkt aufstellen
können
A(-3/1/2), B(-1/0/4), C(2/5/2)
Wissen, was durch das vektorielle
Produkt zweier Vektoren bestimmt
wird?
Antwort:
Ges.: AB x AC :
Wissen, wie Gerade und Ebene
Wie liegen die Ebene und die Gerade
zueinander liegen können.
zueinander:
Lagebeziehung zw. Gerade und Ebene
: 2x – 3y + 7z = 2
bestimmen können
5 
3 
 
 
g : 
   9   s.  5 
X
15 
7 
 
 
Wissen, wie zwei Ebene zueinander
liegen können.
Wie liegen die zwei Ebenen
zueinander:
Lagebeziehung zwischen zwei
Ebenen bestimmen können
1: x – 5y – 4z = -23
Wissen, wie drei Ebene zueinander
liegen können.
Wie liegen die drei Ebenen
zueinander:
2: x – 2y – z = -8
Lagebeziehung zwischen drei Ebenen 1: 2x – 3y + 5z = 23
bestimmen können
2: x + y – 2z = -7
3: x – 2y – 3z = -4
Winkel zwischen Vektoren berechnen Gegeben: A(1/-3), B(5/1), C(1/3).
können
Bestimme den Winkel zwischen AB
und AC :
Winkel zwischen Gerade und Ebene
berechnen können
Bestimme den Winkel zwischen
: 4x + y - 6z = 8 und der
1   0 
   
Gerade g: 

  2   t.  3
X
3   2 
   
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „6. Klasse Vektorrechnung“ können solltest:
Winkel zwischen zwei Ebenen
berechnen können
Bestimme den Winkel zwischen
: 4x + y - 6z = 8 und
1   0 
1 
   
 
: 


2

t
.

3

s
.




 2
X
3   2 
3
   
 
Längen mittels vektorieller Projektion Gegeben: A(2/1/-3), B(5/2/1),
berechnen können
C(1/3/-2).
Bestimme die Normalprojektion des
Vektors AB auf AC !
Formeln zur Berechnung des
Flächeninhalts von Parallelogramm
und Dreieck anwenden können
Gegeben: A(2/1/-3), B(5/2/1),
C(1/3/-2). Bestimme den Flächeninhalt des Dreiecks ABC.
Volumen des Parallelepipeds und der
Pyramide berechnen können
Gegeben: Pyramide mit Grundfläche
= Parallelogramm
A(-5/2/3), B(-1/-2/1), C(3/5/0), D,
S(13/0,5/20,5). Bestimme das
Volumen der Pyramide.
Abstand zwischen Punkt und Gerade
in R2 berechnen können
Geg.: A(4/3), g: y= ½ x + 3
Ges.: Normalabstand des Punktes von
der Geraden
Abstand zwischen Punkt und Ebene in Geg: Pyramide A(-1/2/-1), B(0/3/-2),
R3 berechnen können
C(4/2/1), S(0/2/3)
Ges.: Länge der Pyramidenhöhe h
Abstand zwischen Punkt und Gerade
in R3 berechnen können
Geg: Dreieck A(-1/2/-1), B(0/3/-2),
C(-4/2/1)
Ges.: Länge der Höhe hc
Abstand zwischen zwei windschiefen
Geraden berechnen können
 2
2 
 
 
g1: 

2

s
.


3 
X
1 
  1
 
 
 0   2
   
g2: 
  0   t. 2 
X
  1  3 
   
Berechne den (kürzesten) Abstand der
Geraden!
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002
Was du beim Kapitel „6. Klasse Vektorrechnung“ können solltest:
TEST zu „VEKTORRECHNUNG 6. KLASSE“
1. Löse folgendes Gleichungssystem und gib eine geometrische Interpretation:
x + 2y – z = 10
4x + 5y – 3z = 27
2x + 3y – z = 23
2. Gib den Abstand der windschiefen Geraden an:
5 
4 
 
 
g: 
   2   s.  1
X
 3
0 
 
 
6  4 
   
h: 
 10   t. 7 
X
1    4 
   
3. Gegeben sind die Punkte A(1|2|0), B(1|4|0), C(5|2|2) und S(1|2|4) einer dreiseitigen
Pyramide mit dem Dreieck ABC als Grundfläche und dem Punkt S als Spitze.
a) Zeige, dass das Dreieck ABC rechtwinkelig ist und bestimme die Größen der übrigen
Winkel des Dreiecks.
b) Ermittle eine Gleichung der Ebene , in der die Punkte A, B und C liegen, in
Normalvektorform.
c) Berechne das Volumen der Pyramide.
d) Bestimme den Winkel zwischen der Kante AS und der Seite AB.
4. Gegeben ist die Ebene x + y + z = 5 und der Punkt P(1/-2/3).
a) Berechne des Abstand des Punktes von der Ebene.
b) Gib die Koordinaten des an der Ebene gespiegelten Punktes an.
LZK 6. Klasse
erstellt von vhs21/elopaIII/Renate Tanzberger
2002