Eindimensionale harmonische Schwingungen

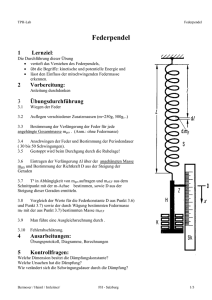
Robert Wichard Pohl, 1884 - 1976
Inhaltsverzeichnis
II Schwingungslehre
2
3
Eindimensionale harmonische Schwingungen . . . . . . . . . . . . . . . . . . . .
3
2.1
Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2.2
Standard-Modell – Feder-Masse-System oder Federpendel . . . . . . . . .
4
2.2.1 Differentialgleichung ungedämpfter harmonischer Schwingungen . .
4
2.2.2 Lösung der Differentialgleichung . . . . . . . . . . . . . . . . . . . .
6
2.2.3 Auslenkung, Geschwindigkeit und Beschleunigung . . . . . . . . . .
9
2.2.4 Energiebetrachtungen . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.3
Weitere Beispiele für ungedämpfte harmonische Bewegungen . . . . . . . 16
2.3.1 Physikalisches Pendel bei kleinen Auslenkungen . . . . . . . . . . . 16
2.3.1.1 Aufstellen der Differentialgleichung . . . . . . . . . . . . . . 18
2.3.1.2 Linearisieren der Differentialgleichung . . . . . . . . . . . . 19
2.3.1.3 Lösung der Differentialgleichung . . . . . . . . . . . . . . . 20
2.3.2 Mathematisches Pendel bei kleinen Auslenkungen . . . . . . . . . . 20
2.3.3 Torsions- oder Drehpendel . . . . . . . . . . . . . . . . . . . . . . . 21
2.3.3.1 Aufstellen der Differentialgleichung . . . . . . . . . . . . . . 22
2.3.3.2 Lösung der Differentialgleichung . . . . . . . . . . . . . . . 23
2.3.4 Analogien Federpendel – Torsionspendel . . . . . . . . . . . . . . . 23
3
2 Eindimensionale harmonische Schwingungen und
ungedämpfte harmonische Schwingungen
Lernziele
• Die Modell-Systeme Feder-Masse-Pendel, Physikalisches Pendel und Drehpendel in
Worten beschreiben und in mathematischer Notation umsetzen.
• Aufstellen der Differentialgleichungen idealisierend ohne Dämpfung nachvollziehen und
Ergebnisse/Beziehungen in Übungsaufgaben umsetzen.
• Grenzen einer sinnvollen Linearisierung angeben und interpretieren.
• Energiebetrachtungen mathematisch formalisieren und in Diagrammen darstellen.
• Vorgegebene Anfangsbedingungen einer Schwingung zur Bestimmung der Integrationskonstanten umsetzen.
2.1 Einleitung
Die Differentialgleichung ungedämpfter harmonischer Bewegungen lautet
ÿ + ω02 y = 0.
Für ein eindimensionales, schwingungsfähiges System ist die Lösungsfunktion das AuslenkungsZeit-Gesetz
y(t) = ŷ cos(ω0 t + ϕ0c ).
In diesem Abschnitt wird untersucht, welche physikalischen Systeme und ihre Bewegungen
durch die obige Differentialgleichung beschrieben werden. Es wird sich ergeben, dass dafür
die beiden folgenden Voraussetzungen notwendig und hinreichend sind:
• Reibungsfreiheit, d. h., es treten keine Widerstands-, Reibungs- oder Dämpfungskräfte
von außen auf.
• Lineares Kraftgesetz (Hookesches Gesetz), die Rückstellkraft auf einen Körper ist
proportional zur Auslenkung aus der Ruhelage des Körpers.
In realen physikalischen Systemen gibt es stets Dämpfung. Diese Dämpfung ist aber in vielen
Fällen sehr schwach, so dass sie – zumindest in erster Näherung – vernachlässigt werden darf.
Der Einfluss der Dämpfung auf die Bewegungsform wird getrennt diskutiert.
In realen physikalischen Systemen ist die Rückstellkraft stets nur näherungsweise proportional zur Auslenkung. Aber für sehr viele Systeme ist diese Näherung recht gut. In mechanischen Systemen gilt z. B. für die Dehnung bzw. Stauchung, für Verbiegen oder Verdrillen
(oder eine Überlagerung all dieser Deformationen) bei nicht zu großen Deformationen in
guter Näherung die geforderte Linearität. Die Erfüllung der genannten Bedingungen führt
stets zu ungedämpften harmonischen Schwingungen.
Als mechanisches Standard-Modell wird zunächst ein Feder-Masse-System oder Federpendel betrachtet: Eindimensionale (oder lineare) Schwingungen eines Körpers der Masse m,
befestigt an einer masselosen Feder, deren Rückstellkraft linear von der Verlängerung bzw.
Eindimensionale harmonische Schwingungen
4
Verkürzung y der Feder abhängt. Die Eigenschaft einer Feder wird durch die Federkonstante
oder Federsteifigkeit k beschrieben.
Ergänzend werden später weitere Beispiele gebracht. Dabei wird auch die Grenze des Gültigkeitsbereiches der idealisierenden Modellvorstellungen, insbesondere der Linearität, diskutiert.
2.2 Standard-Modell – Feder-Masse-System oder Federpendel
2.2.1 Differentialgleichung ungedämpfter harmonischer Schwingungen
Um den Einfluss der Gravitationskraft zu kompensieren, befestigt man einen Körper der
Masse m waagerecht schwingungsfähig an einer Feder (vgl. Abb. 2-01).
Felast = 0
m
reibungsfrei
Ruhelage
Felast = −ky
m
0
y
Abb. 2-01: Standard-Modell für ungedämpfte harmonische Schwingungen: Feder-MasseSystem ( Federpendel) ohne Reibung.
Oberes Teilbild: Feder entspannt, Ruhelage der Feder bei der Koordinate y = 0 m.
Unteres Teilbild: Feder aus der Ruhelage um y ausgelenkt.
Für die horizontale Bewegung wirkt auf den Körper in y-Richtung allein die Rückstellkraft
Felast der gedehnten bzw. gestauchten Feder.
Dem Feder-Masse-System liegen dabei die folgenden Modellvorstellungen zugrunde:
• Die Charakteristik der Feder folgt einem linearen (Hookeschen) Kraftgesetz.
• Die Feder hat keine Masse: D. h., die einzelnen Massenelemente der Feder brauchen
weder beschleunigt noch abgebremst zu werden, deshalb muss ihre kinetische Energie
nicht berücksichtigt werden.
• Es treten keine äußeren Widerstandskräfte auf: D. h., der Körper (Masse m) soll sich
auf der Unterlage reibungsfrei bewegen.
Eindimensionale harmonische Schwingungen
5
Es gilt ein lineares Kraftgesetz nach Hooke: Die elastische Rückstellkraft ist gegeben durch
Felast = −ky.
Man nennt die Proportionalitätskonstante dieses Kraftgesetzes die Federkonstante der Feder
(Formelbuchstabe k). Es sind auch die Bezeichnungen Federsteifigkeit oder Federkoeffizient
(alte Formelbuchstaben D oder c) gebräuchlich. Die Rückstellkraft der Feder ist die einzige
Kraft, die in y-Richtung auf den Körper einwirkt. Die Gewichtskraft wird durch die Unterlage
kompensiert.
Nach dem Newtonschen Aktionsprinzip bewirkt eine Kraft auf einen Körper dessen Beschleunigung gemäß
F = ma = mÿ.
In y-Richtung wirkt auf den Körper nur die Rückstellkraft. Unter der Verwendung des
linearen Kraftgesetzes erhält man
−ky = mÿ
mÿ + ky = 0
k
ÿ + y = 0.
m
Dies ist aber genau die Form der Differentialgleichung, die in Abschnitt 1 für eine ungedämpfte harmonische Bewegung hergeleitet wurde. Die zu Grunde liegende Voraussetzung
für die mathematische Form der Differentialgleichung ist ein lineares Kraftgesetz. Diese Aussage lässt sich auch umkehren: Wenn eine Differentialgleichung vom obigen Typ gilt, dann
gilt notwendigerweise ein lineares Kraftgesetz.
Vertikale Schwingungen (vgl. Abb. 2-02)
Für vertikale Schwingungen stimmt die statische Ruhelage ystat des angehängten Körpers
(Masse m) nicht mit der Nulllage y = 0 m der entspannten Feder überein. Die Gewichtskraft
auf den Körper bewirkt lediglich eine Vorspannung der Feder. Diese Vorspannung wirkt sich
aber nicht auf die Eigenkreisfrequenz ω0 aus, solange die Kennlinie der Feder linear ist.
Die Ruhelage der entspannten, idealen Feder liegt bei der Koordinate y = 0 m. Die statische
Ruhelage (bei angehängtem Körper) des schwingungsfähigen Systems stellt sich bei y = ystat
ein. Die Gleichgewichtsbedingung fordert
FG + Felast = 0.
Gewichtskraft FG = mg (nach unten, positive y-Richtung).
Elastische Rückstellkraft der Feder Felast = −kystat (nach oben, negative y-Richtung).
Die statische Gleichgewichtsbedingung lautet
mg − kystat = 0.
Für eine zusätzliche Auslenkung um y aus der statischen Ruhelage y = ystat wird die Gesamtauslenkung der Feder (ystat + y) und damit die Gesamt-Rückstellkraft der Feder
Felast = −k(ystat + y)
Eindimensionale harmonische Schwingungen
6
und die Gesamtkraft auf den Körper
Fges = Felast + FG = −k(ystat + y) + mg
= (−kystat + mg) − ky = 0 − ky = −ky,
dabei wurde die statische Gleichgewichtsbedingung berücksichtigt. Mit dem Newtonschen
Aktionsgesetz ergibt sich daraus sofort die Differentialgleichung der ungedämpften harmonischen Bewegung.
0
Felast = −kystat
Felast = −k(ystat + y)
ystat
FG = mg
(ystat + y)
Auslenkung
FG = mg
Abb. 2-02: Vertikale Schwingungen nahe der Erdoberfläche.
2.2.2 Lösung der Differentialgleichung
Die mathematische Form der Differentialgleichung ist identisch mit der in Abschnitt 1.4
dargestellten Gleichung. Deshalb lassen sich sämtliche dort hergeleiteten Aussagen direkt
auf das Modell des Feder-Masse-Systems übertragen.
Der Vergleich der beiden Darstellungen ergibt:
In der Differentialgleichung ist der konstante Koeffizient
Quadrat der Eigenkreisfrequenz ω02 .
k
vor der Funktion y gleich dem
m
k
m
Mit der Beziehung
2π
ω0 =
T0
erhält man damit für die Schwingungsdauer T0 des Standard-Modells eines Feder-MasseSystems
m
T0 = 2π
.
k
ω02 =
Eindimensionale harmonische Schwingungen
7
Die Schwingungen, also das physikalische Verhalten des Systems, werden eindeutig durch die
Masse m des angehängten Körpers und der Federkonstanten k der idealen Feder festgelegt.
Masse m und Federkonstante k bestimmen eindeutig die Eigenkreisfrequenz ω0 (bzw. die
Eigenfrequenz f0 oder die Schwingungsdauer T0 ) des Systems. Mit dieser Eigenkreisfrequenz
ω0 antwortet das System auf einen einmaligen Anstoß. Man spricht in diesem Fall von freien
Schwingungen.
Das Auslenkungs-Zeit-Gesetz kann dargestellt werden durch eine Kosinus-Funktion
y(t) = ŷ cos(ω0 t + ϕ0c )
oder eine Sinus-Funktion
y(t) = ŷ sin(ω0 t + ϕ0s ).
Vorsicht: Die Nullphasenwinkel ϕ0c und ϕ0s sind für die beiden Beschreibungen notwendigerweise verschieden!
Als allgemeine Lösung einer linearen Differentialgleichung 2. Ordnung enthält neben der
systemcharakteristischen Eigenkreisfrequenz ω0 zwei zunächst noch beliebige Integrationskonstanten, nämlich eine Amplitude ŷ und einen Nullphasenwinkel ϕ0 (ϕ0c bzw. ϕ0s ). Dies
ergibt eine ganze Schar von Lösungsfunktionen.
Zur Bestimmung der Lösungsfunktion in einem konkreten Fall müssen notwendigerweise
noch zwei weitere Bedingungen herangezogen werden. Meist wählt man die Anfangsbedingungen zum Zeitpunkt t = 0 s, also
Auslenkung y(t = 0 s) = y(0) und Geschwindigkeit v(t = 0 s) = v(0).
Die Masse m des Körpers und die Federkonstante k der Feder legen die Eigenkreisfrequenz ω0
eindeutig fest. Dabei sind aber Amplitude ŷ und Nullphasenwinkel ϕ0 noch beliebig wählbar.
Ist aber die Bewegung des Systems einmal, bei vorgegebenen Anfangsbedingungen, gestartet,
dann müssen auch ŷ und ϕ0 ebenso eindeutig festliegen.
Berücksichtigt man die Anfangsbedingungen, dann kann eine Schwingung eindeutig als Funktion der Zeit beschrieben werden.
Die anschauliche Bedeutung der drei physikalischen Größen Eigenkreisfrequenz ω0 , Amplitude ŷ und Nullphasenwinkel ϕ0 und ihren Einfluss auf die Lösungsfunktion der Differentialgleichung einer ungedämpften harmonischen Bewegung sind in den folgenden Abbildungen
dargestellt.
Eindimensionale harmonische Schwingungen
8
Zwei identische Feder-Masse-Systeme – Eigenkreisfrequenzen ω01 = ω02 = ω0
y
ŷ1
y1 (t)
y2 (t)
t
T1
−ŷ1
Die beiden Lösungen haben identische Amplituden ŷ1 = ŷ2 = ŷ.
Die beiden Lösungen unterscheiden sich in ihren Nullphasenwinkeln
π
ϕ01 = 0 und ϕ02 = .
6
Die zugehörigen Bewegungsgleichungen sind
π
.
y1 (t) = ŷ cos(ω0 t) und y2 (t) = ŷ cos ω0 t +
6
Zwei identische Feder-Masse-Systeme – Amplituden ŷ3 = ŷ1
y
y1 (t)
ŷ1
ŷ3
y3 (t)
T1
−ŷ3
−ŷ1
Die beiden Lösungen haben identische Nullphasenwinkel ϕ01 = ϕ03 = 0.
Die beiden Lösungen unterscheiden sich in ihren Amplituden
2
ŷ3 = ŷ1 = ŷ.
3
Die zugehörigen Bewegungsgleichungen sind
3
y1 (t) = ŷ cos(ω0 t) und y3 (t) = ŷ cos(ω0 t).
2
t
Eindimensionale harmonische Schwingungen
9
Zwei verschiedene Feder-Masse-Systeme – Eigenkreisfrequenzen ω01 = ω04
Für die Eigenkreisfrequenzen gilt ω04 = 2ω01 = 2ω0 .
y
ŷ1
y4 (t)
y1 (t)
t
T4
T1
−ŷ1
Die beiden Lösungen haben identische Amplituden ŷ1 = ŷ4 = ŷ.
Die beiden Lösungen haben identische Nullphasenwinkel ϕ01 = ϕ04 = 0.
Die zugehörigen Bewegungsgleichungen sind
y1 (t) = ŷ cos(ω0 t) und
y4 (t) = ŷ cos(2ω0 t).
2.2.3 Zusammenhang zwischen Auslenkung, Geschwindigkeit und Beschleunigung eines schwingenden Körpers
Eine ungedämpfte harmonische Bewegung wird beschrieben durch
y(t) = ŷ cos(ω0 t + ϕ0 ).
Da zur Beschreibung eine Kosinus-Funktion gewählt wird, ist die Angabe des Nullphasenwinkels mit ϕ0 eindeutig, auf die Indizierung ϕ0c wird deshalb verzichtet.
Ein- bzw. zweimalige Differentiation dieser Funktion nach der Zeit t liefern die Geschwindigkeit v = ẏ und die Beschleunigung a = ÿ.
v(t) = ẏ(t) = −ŷω0 sin(ω0 t + ϕ0 )
a(t) = ÿ(t) = −ŷω02 cos(ω0 t + ϕ0 ) = −ω02 y(t)
Die Integrationskonstanten ŷ und ϕ0 lassen sich bestimmen, wenn für die Zeit t = 0 s die
zugehörigen Anfangsbedingungen y(0) und v(0) vorgegeben werden.
Beispiel zur Bestimmung der Integrationskonstanten
Der Körper (Masse m) wird zunächst um yanf aus der Ruhelage ausgelenkt und anschließend
zum Zeitpunkt t = 0 s ohne Anfangsgeschwindigkeit losgelassen. Damit sind die Anfangsbedingungen
y(0) = yanf
und
v(0) = ẏ(0) = 0.
Einsetzen dieser Anfangsbedingungen liefert zwei Bestimmungsgleichungen für Amplitude ŷ
und Nullphasenwinkel ϕ0 .
yanf = ŷ cos(ϕ0 )
0 = −ŷω0 sin(ϕ0 )
Eindimensionale harmonische Schwingungen
10
Die zweite Gleichung ist dann und nur dann erfüllt, wenn wenigstens einer der drei Faktoren
null ist. Die Amplitude ŷ und die Eigenkreisfrequenz ω0 können bei einer Schwingung nicht
null sein. Es folgt notwendig sin(ϕ0 ) = 0 und damit wird der Nullphasenwinkel (in der
Darstellung der Schwingungen als Kosinus-Funktion)
ϕ0 = 0.
Dieses Ergebnis in die erste Bedingungsgleichung eingesetzt, liefert für die Amplitude
yanf = ŷ cos(0) = ŷ.
Damit lautet die Lösung der Differentialgleichung für alle Zeiten t für die im Beispiel vorgegebenen Anfangsbedingungen (Auslenken um yanf aus der Ruhelage und anschließendes
Loslassen ohne Anfangsgeschwindigkeit )
y(t) = ŷ cos ω0 t.
Wie im behandelten Beispiel wird für weitere Diskussionen ein Nullphasenwinkel ϕ0 = 0
gewählt. Dies vereinfacht die mathematische Beschreibung, ändert aber nichts an der Allgemeingültigkeit der Ergebnisse.
Die harmonischen Funktionen sind auf den Wertebereich zwischen (−1) und (+1) beschränkt,
denn
−1 ≤ sin(ω0 t) ≤ 1
und
− 1 ≤ cos(ω0 t) ≤ 1.
Deshalb gilt für die Beträge der Maximalwerte von Auslenkung y, Geschwindigkeit v und
Beschleunigung a
•
Auslenkung:
ymax = | ± ŷ|,
•
Geschwindigkeit:
vmax = | ± ŷω0 |,
•
Beschleunigung:
amax = | ± ŷω02 |.
In Abb. 2-03 sind die Zeitabhängigkeiten von Auslenkung y(t), Geschwindigkeit v(t) und
Beschleunigung a(t) vereinfachend für einen Nullphasenwinkel ϕ0 = 0 graphisch dargestellt.
Für spezielle Bahnpunkte erhält man für die Beträge (vgl. Abb. 2-03):
Beim Durchgang durch die Ruhelage, also für y = 0 m, ist
• die Geschwindigkeit v = vmax ,
• die Beschleunigung a = 0 m s−2 und damit auch F = 0 N
(in Übereinstimmung mit Felast = −ky = 0 N für y = 0 m).
In den Umkehrpunkten, also für die Auslenkung y = ±ŷ,
• ist die Geschwindigkeit v = 0 m s−1
(die Geschwindigkeit wechselt ihre Richtung),
• ist die Beschleunigung a = amax
(in Übereinstimmung mit Felast = −kŷ für y = ŷ).
In Abb. 2-04 sind für ausgewählte Bahnpunkte für eine Periode die Auslenkung y, die Geschwindigkeit v, die Beschleunigung a und die nach Newton zur Beschleunigung proportionale Kraft F eingetragen.
Eindimensionale harmonische Schwingungen
11
y
ŷ
t
v = ẏ
ω0 ŷ
t
a = ÿ
ω02 ŷ
t
Abb. 2-03: Ungedämpfte harmonische Schwingungen.
Für ein ideales Feder-Masse-System sind dargestellt:
Auslenkungs-Zeit-Gesetz:
y(t) = ŷ cos(ω0 t),
Geschwindigkeits-Zeit-Gesetz:
v(t) = ẏ(t) = −ŷω0 sin(ω0 t),
Beschleunigungs-Zeit-Gesetz:
a(t) = ÿ(t) = −ŷω02 cos(ω0 t).
Der Nullphasenwinkel ϕ0 wurde dabei vereinfachend gleich null gesetzt (diese Setzung schränkt
die Allgemeingültigkeit nicht ein).
Hinweis:
Beachten Sie die verschiedenen Einheiten auf den Ordinatenachsen!
Eindimensionale harmonische Schwingungen
12
Die harmonischen Funktionen sind auf den Wertebereich zwischen (−1) und (+1) beschränkt,
denn
−1 ≤ sin(ω0 t) ≤ 1
und
− 1 ≤ cos(ω0 t) ≤ 1.
Deshalb gilt für die Beträge der Maximal/Minimalwerte von Auslenkung y, Geschwindigkeit
v und Beschleunigung a
Auslenkung:
ymax / min = ±ŷ,
Geschwindigkeit:
vmax / min = ±ŷω0 ,
Beschleunigung:
amax / min = ±ŷω02 .
Für ausgewählte Bahnpunkte (Umkehrpunkte und Ruhelage) sind die Auslenkung y, die
Geschwindigkeit v, die Beschleunigung a und die auf den Körper (Masse m) wirkende Kraft
Felast (ausgeübt von der Feder) eingetragen (vgl. Abb. 2-04). Die Richtungen der vektoriellen
Größen sind durch Pfeile angegeben, ihre Beträge sind als skalare Größen eingetragen.
Vergleichen Sie mit der Darstellung in Abb. 2-03.
Das Auslenkungs-Zeit-Gesetz lautet
y(t) = ŷ cos(ω0 t),
d. h., der Nullphasenwinkel ϕ0 wurde – ohne Beschränkung der Allgemeinheit – vereinfachend gleich null gesetzt.
y
+ŷ
Felast = −kŷ
a = −ω02 ŷ
t
0
v = −ω0 ŷ
v = ω0 ŷ
−ŷ
Felast = kŷ
y = −ŷ
v=0
Felast = kŷ
a = ω02 ŷ
y=0
Felast = 0
a=0
y = +ŷ
v=0
y=0
Felast = 0
a=0
a = ω02 ŷ
y = −ŷ
v=0
Abb. 2-04: Ungedämpfte harmonische Schwingungen eines idealen Feder-Masse-Systems
(reibungsfrei auf horizontaler Unterlage, vgl. Abb. 2-01).
Eindimensionale harmonische Schwingungen
13
Energieinhalt einer idealen Feder
Durch Stauchen oder Dehnen wird an einer Feder Arbeit verrichtet, die als potentielle Energie in der Feder gespeichert wird. Diese gespeicherte Energie kann Arbeit verrichten.
Die für eine differentielle Änderung dy der Federlänge durch eine äußere Kraft Fext aufzuwendende Arbeit dW ist als skalares Produkt definiert
dW (y) = Fext (y) · d
y.
Die äußere Kraft Fext muss dabei der Rückstellkraft Felast der Feder stets das Gleichgewicht
halten, also gilt für die Beträge (eindimensionales Problem)
Fext + Felast = 0
Fext = −Felast = −(−ky) = ky.
Da die externe Kraft Fext parallel zur Auslenkung y gerichtet ist, gilt
cos(Fext ,y ) = 1.
Damit wird die insgesamt gegen die Federkraft aufzuwendende Arbeit W12 bei einer Dehnung
der Feder von y1 auf y2
y2
y2
W12 = Fext (y) dy = ky dy
y1
W12
y1
y
1 2 2
1
= ky = k(y22 − y12 ).
2
2
y1
Feder
in der Feder gespeichert.
Die aufgewendete Arbeit W12 ist als potentielle Energie Epot
Setzt man speziell y1 = 0 m, d. h., man bezieht die Längenänderungen der Feder auf ihre
entspannte Nulllage, dann ist die potentielle Energie der Feder allgemein gegeben durch die
Beziehung
1
Feder
= ky 2 .
Epot
2
Feder
einer
Als Abhängigkeit von der Auslenkung y erhält man für die potentielle Energie Epot
idealen Feder eine Parabel 2. Ordnung, deren Öffnung durch die Federkonstante k bestimmt
wird.
In Abb. 2-05 sind graphisch dargestellt:
Feder
Die potentielle Energie Epot
einer idealen Feder in Abhängigkeit von der Auslenkung y
Feder
aus der Ruhelage. Die potentielle Energie Epot
hängt quadratisch von der Auslenkung y
ab. Sie hat in den beiden Umkehrpunkten y = ±ŷ ihren Maximalwert.
Dieser Wert ist dabei gleich der Gesamtenergie des Feder-Masse-Systems, weil in den UmKörper
kehrpunkten (wegen v = 0 m s−1 ) auch die kinetische Energie Ekin
= 0 J ist (Teilbild
(a)).
Die Rückstellkraft Felast in (linearer) Abhängigkeit von der Auslenkung y aus der Ruhelage.
Für Auslenkungen in positiver (negativer) y-Richtung ist die Kraft in negative (positive)
y-Richtung gerichtet (Teilbild (b)).
Eindimensionale harmonische Schwingungen
14
Feder
(y)
Epot
Feder
Epot
(y)
=
1
2
2 ky
(a)
y
−ŷ
Felast (y) = −ky
ŷ
Felast (y)
y
(b)
−ŷ
ŷ
Abb. 2-05: Lineares Kraftgesetz und Energieinhalt einer idealen Feder.
Für das Modell eines Feder-Masse-Systems sind in Abhängigkeit von der Auslenkung y aus
der Ruhelage dargestellt:
Feder
(a): Die potentielle Energie Epot
der Feder ( Parabelpotential).
(b): Die auf den Körper der Masse m wirkende Kraft Felast .
2.2.4 Energiebetrachtungen
Da im Modell keine Widerstandskräfte auftreten, ist ein Einfluss von Reibungsverlusten
nicht zu berücksichtigen, es muss notwendig der Energieerhaltungssatz in der Schreibweise
der Mechanik gelten, also
Körper
System
Feder
Eges
= Ekin
+ Epot
= konst.,
dabei ist die kinetische Energie des schwingenden Körpers gegeben durch
1
1
Körper
Ekin
= mv 2 = mẏ 2
2
2
und die potentielle Energie der gedehnten oder gestauchten Feder durch
1
Feder
Epot
= ky 2 .
2
Eindimensionale harmonische Schwingungen
15
Einsetzen für das Auslenkungs-Zeit-Gesetz und das Geschwindigkeits-Zeit-Gesetz ergibt
1
Feder
= kŷ 2 cos2 (ω0 t + ϕ0 )
Epot
2
1
Feder
Ekin = mŷ 2 ω02 sin2 (ω0 t + ϕ0 ),
2
mit der Beziehung für die Eigenkreisfrequenz
k
ω02 =
m
ergibt sich für die kinetische Energie
1
1
Körper
= kŷ 2 sin2 (ω0 t + ϕ0 ) = kŷ 2 [1 − cos2 (ω0 t + ϕ0 )]
Ekin
2
2
1
1
1
= kŷ 2 − ky 2 = k(ŷ 2 − y 2 ).
2
2
2
Da die Quadrate der harmonischen Funktionen auf den Wertebereich (0) bis (+1) beschränkt
sind, also
0 ≤ sin2 α ≤ 1
und
0 ≤ cos2 α ≤ 1
gilt,
ergeben sich für die beiden Energiebeiträge die Bedingungen
1
1
Körper
Feder
0 ≤ Epot
≤ kŷ 2 und 0 ≤ Ekin
≤ kŷ 2 .
2
2
Für die Gesamtenergie erhält man bei der vorausgesetzten Reibungsfreiheit den erwarteten
konstanten Wert
1
System
= kŷ 2 [sin2 (ω0 t + ϕ0 ) + cos2 (ω0 t + ϕ0 )]
Eges
2
1 2 1
System
Eges
= kŷ = mŷ 2 ω02 = konst.
2
2
Es ist charakteristisch für eine ungedämpfte harmonische Schwingung, dass die Gesamtenergie Eges proportional zum Quadrat der Amplitude ŷ der harmonischen Schwingung ist.
System
Feder
Die (konstante) Gesamtenergie Eges
, die potentielle Energie Epot
und die kinetische
Körper
Energie Ekin
können gegen die Ortskoordinate y oder gegen die Zeit t aufgetragen werden.
Diese beiden Darstellungen sind in Abb. 2-06 gezeichnet.
E(t)
System
Eges
Feder
Epot
(a)
E = E(t)
Körper
Ekin
t
1
2 T0
T0
Eindimensionale harmonische Schwingungen
16
E(y)
System
Eges
Feder
Epot
(b)
E = E(y)
Körper
Ekin
y
ŷ
−ŷ
Abb. 2-06: Energiebetrachtungen – ungedämpfte harmonische Schwingungen.
Teilbild (a): Energieverhältnisse in Abhängigkeit von der Zeit t.
Teilbild (b): Energieverhältnisse in Abhängigkeit von der Auslenkung y.
Beispiel: Schwingungen beschrieben durch die Funktion y(t) = ŷ cos(ω0 t) (Auslenken des
Körpers und Loslassen ohne Anfangsgeschwindigkeit).
•
Potentielle Energie der Feder:
Feder
= 12 ky 2
Epot
•
Kinetische Energie des Körpers:
Körper
Ekin
= 12 mv 2 = 12 mẏ 2
•
(Konstante) Gesamtenergie:
Körper
System
Feder
Eges
= Ekin
+ Epot
= konst.
2.3 Weitere Beispiele für ungedämpfte harmonische Bewegungen
Es werden im Folgenden einige weitere, einfache physikalische Systeme betrachtet, deren
Verhalten jeweils durch die Differentialgleichung ÿ = −ω02 y einer ungedämpften harmonischen Schwingung beschrieben wird. Deshalb können sämtliche Ergebnisse aus Abschnitt
1.4 direkt übernommen werden. Insbesondere wird die Näherung für die Gültigkeit eines
linearen Kraftgesetzes diskutiert.
2.3.1 Physikalisches Pendel bei kleinen Auslenkungen
Die Definition eines physikalischen Pendels ist:
Ein physikalisches (oder physisches) Pendel ist ein starrer Körper beliebiger Massenverteilung, der im Schwerefeld der Erde so aufgehängt ist, dass er in einer
vertikalen Ebene um eine Achse, die nicht durch seinen Massenmittelpunkt geht,
unter dem Einfluss der Gravitationskraft schwingen kann.
Massenträgheitsmoment
Für die Behandlung eines physikalischen Pendels braucht man Kenntnisse über Drehbewegungen aus der Mechanik, also die Übersetzung der Newtonschen Gesetzmäßigkeiten von
Translationsbewegungen auf Rotationsbewegungen. Ohne Beweis werden die Grundlagen
kurz skizziert:
Eindimensionale harmonische Schwingungen
17
Übersetzungstabelle
Translation
Rotation
Kraft F
vektoriell, dazu Betrag und
Drehmoment M
Rechtsschraubenrichtung
Massenträgheitsmoment J
Winkelbeschleunigung α
M = Jα
Masse m
Beschleunigung a
F = ma
Das Massenträgheitsmoment J eines materiellen Teilchens der Masse Δm, das im Abstand
r um eine vorgegebene Drehachse umläuft, ist definiert als
J = Δmr2 .
Für einen räumlich ausgedehnten starren Körper hängt das Massenträgheitsmoment J von
der Geometrie der Verteilung der Massenelemente um eine gewählte Rotationsachse ab.
Die Summierung über sämtliche Massenelemente J = Δmi ri2 liefert im Grenzübergang das
Integral über den Gesamtkörper.
r2 dm
J=
Körper
In Tabellenwerken finden sich Massenträgheitsmomente JS bzgl. Drehachsen durch den Massenmittelpunkt S eines Körpers (Index ‘S’ für Schwerpunkt).
Der Steinersche Satz erlaubt es, das Massenträgheitsmoment JP für eine Drehachse durch
einen Punkt P auf eine dazu parallele Achse durch den Schwerpunkt S zurückzuführen. Es
gilt
JP = JS + md2 .
Dabei ist d der Abstand der beiden parallelen Achsen durch P und S und m die Gesamtmasse
des Körpers.
S
d
P
Eine Darstellung eines physikalischen Pendels und eine Auflistung der im Folgenden benutzten Nomenklatur findet sich in Abb. 2-07.
Eindimensionale harmonische Schwingungen
18
2.3.1.1 Aufstellen der Differentialgleichung
Bei der Auslenkung des Körpers um den Winkel β aus der Ruhelage übt die Gewichtskraft FG
elast auf den Körper aus. Dieses Drehmoment versucht, den Körper
ein Rückstellmoment M
in die Ruhelage β = 0 zurückzutreiben.
Der Betrag des Rückstellmoments ergibt sich unter Berücksichtigung der Geometrie (vgl.
Abb. 2-07)
Melast = −mgd sin β.
Ein Drehmoment M bezüglich des Drehpunkts P bewirkt nach Newton eine Winkelbeschleunigung α gemäß
d2 β
= JP β̈.
dt2
Man erhält nach Einsetzen von Melast
M = JP α = J P
−mgd sin β = JP β̈
oder nach Umstellen die Differentialgleichung
mgd
sin β = 0.
β̈ +
JP
In dieser Differentialgleichung ist der zweite Ausdruck proportional zum Sinuswert des Auslenkwinkels β, nicht aber zum Auslenkwinkel β. Diese Gleichung hat also nicht die mathematische Form der Differentialgleichung der ungedämpften harmonischen Schwingung. Im
allgemeinen Fall wird sich deshalb keine harmonische Schwingung einstellen.
P
d
d
g
S×
β
FG
Abb. 2-07: Physikalisches (physisches) Pendel – Modell und benutzte Nomenklatur.
= d × FG
Rücktreibendes Drehmoment M
Richtung: Anwenden der Rechtsschraubenregel: Den Vektor d auf kürzestem Weg in den
in die Zeichenebene hinein (rechtsdrehend).
Vektor FG drehen. Damit zeigt der Vektor M
Betrag: |M | = |d| · |FG | · sin(d,FG ) = mgd sin β
Eindimensionale harmonische Schwingungen
m
P
S
d
d,
JP
β
β=0
β̂
FG
19
Gesamtmasse des Pendelkörpers
Drehpunkt einer horizontal verlaufenden Drehachse (reibungsfrei!)
Massenmittelpunkt
Abstand zwischen Drehachse und Massenmittelpunkt
zeigt d von P
(in einer vektoriellen Darstellung des Drehmoments M
nach S).
Massenträgheitsmoment des Körpers bezüglich der Achse durch P
(momentaner) Auslenkwinkel des Pendels aus der Ruhelage
Ruhelage des physikalischen Pendels: Der Massenmittelpunkt liegt
senkrecht unter dem Drehpunkt P (das entspricht dem Minimum der
potentiellen Energie der Lage des Körpers)
maximaler Auslenkwinkel des Pendels
Gewichtskraft (angreifend im Massenmittelpunkt S)
2.3.1.2 Linearisieren der Differentialgleichung
Eine Sinus-Funktion kann in eine Potenzreihe entwickelt werden
1
1
1
sin β = β − β 3 + β 5 − β 7 + − . . .
3!
5!
7!
Lies im Nenner das Symbol ‘!’ als Fakultät.
Es ist
3! = 3 · 2 · 1
und
5! = 5 · 4 · 3 · 2 · 1
usw.
Für kleine Winkel β können diejenigen Glieder der Potenzreihe, deren Potenz größer als eins
ist, gegen das lineare Glied vernachlässigt werden. Man bricht die Reihe nach dem linearen
Glied ab und ersetzt damit die Sinus-Funktion durch den zugehörigen Winkel (gemessen im
Bogenmaß!).
sin β ≈ β
Dann ist der Betrag des Rückstellmoments Melast näherungsweise proportional zum Auslenkwinkel β und man erhält nach dieser Linearisierung die Differentialgleichung
mgd
β̈ +
β = 0.
JP
Die Auswirkungen der Linearisierung zeigt die folgende Tabelle:
β
Grad
0
2
5
10
15
β
rad
0,0000
0,0349
0,0873
0,1745
0,2618
sin β
Differenz (%)
0,0000
0,0349
0,0872
0,1736
0,2588
0,00
0,00
0,11
0,51
1,14
Eindimensionale harmonische Schwingungen
20
2.3.1.3 Lösung der Differentialgleichung
Diese linearisierte Differentialgleichung hat mathematisch wieder die Form der Differentialgleichung einer ungedämpften harmonischen Schwingung.
Damit erhält man als Lösung sofort die Bewegungsgleichung, also das AuslenkungswinkelZeit-Gesetz
β = β̂ cos(ω0 t + ϕ0 )
und für die Eigenkreisfrequenz durch Koeffizientenvergleich
mgd
ω02 =
.
JP
Die Schwingungsdauer wird
JP
.
T0 = 2π
mgd
Sämtliche hergeleiteten Beziehungen gelten aber selbstverständlich nur unter der gemachten,
einschränkenden Annahme kleiner Auslenkwinkel aus der Ruhelage.
2.3.2 Mathematisches Pendel bei kleinen Auslenkungen
Definition eines mathematischen Pendels:
Ein materieller Punkt der Masse m, der an einem masselosen, nicht dehnbaren Faden der Länge L aufgehängt ist und in einer vertikalen Ebene unter dem
Einfluss der Gravitationskraft schwingen kann.
Nach dieser Definition stellt also das mathematische Pendel eine spezielle Geometrie des
physikalischen Pendels dar. Die Gesamtmasse des Körpers ist in einem materiellen Teilchen
vereinigt, damit liegt auch der Massenmittelpunkt S im materiellen Teilchen. Es ist
• die Fadenlänge L der Abstand d zwischen Drehachse P und Massenmittelpunkt S und
• das Massenträgheitsmoment JP des materiellen Teilchens bezüglich des Drehpunkts P
vereinfacht sich zu JP = mL2 .
Damit ergibt sich für die Eigenkreisfrequenz
mgL
g
=
ω02 =
mL2
L
und für die zugehörige Schwingungsdauer
L
math
.
T0
= 2π
g
Für ein mathematisches Pendel ist die Schwingungsdauer (allerdings nur unter der Näherung
kleine Auslenkwinkel aus der Ruhelage) unabhängig von der Masse m des Pendels.
Realisiert wird das Modell des mathematischen Pendels durch ein Fadenpendel:
• Ein Körper der Masse m ist an einem langen, dünnen Faden aufgehängt.
• Die geometrischen Abmessungen des Körpers sind sehr klein gegen die Fadenlänge L.
Eindimensionale harmonische Schwingungen
21
Diese Beziehung liefert eine einfache Methode zur Bestimmung der Fallbeschleunigung g
(welche vom geographischen Ort an der Erdoberfläche abhängt). Eine genauere Bestimmung
von g ist mit dem Reversionspendel möglich.
Reduzierte Pendellänge
Für jedes physikalische Pendel lässt sich als Ersatzpendel ein mathematisches Pendel angeben, das die gleiche Schwingungsdauer hat wie das physikalische Pendel. Man nennt die
Länge dieses Ersatzpendels die reduzierte Pendellänge Lred.
Die Schwingungsdauer eines physikalischen Pendels um die Achse durch P ist gegeben durch
JP
phys
T0
.
= 2π
mgd
Die Schwingungsdauer eines mathematischen Pendels der Pendellänge Lred ist gegeben durch
Lred
math
.
T0
= 2π
g
Die Forderung identischer Schwingungsdauern für die beiden Pendel verlangt
T0math = T0phys .
Dies ergibt
Lred
JP
=
.
g
mgd
Unter Benutzung des Steinerschen Satzes kann man das Massenträgheitsmoment JP eines
Körpers (Masse m) immer zurückführen auf das Massenträgheitsmoment JS bezüglich einer
dazu parallelen Achse im Abstand d durch den Massenmittelpunkt S.
Es gilt
JP = JS + md2 .
Damit ergibt sich die reduzierte Pendellänge zu
Lred =
JS
JS + md2
=
+ d.
md
md
2.3.3 Torsions- oder Drehpendel
Eine homogene Kreisscheibe ist an einem Aufhängedraht bzw. Aufhängestab, der durch
das Zentrum der Scheibe geht, aufgehängt. Das Verdrehen der Scheibe führt zu einer Verdrillung des Aufhängedrahtes. Dadurch wird ein rückstellendes Drehmoment hervorgerufen,
das versucht, die Scheibe in ihre ursprüngliche Ruhelage zurückzutreiben. Das rückstellende
Drehmoment hängt von den elastischen Eigenschaften der Aufhängung ab. In Abb. 2-08 ist
dieses Modell dargestellt.
Der Aufhängedraht (und seine elastischen Eigenschaften) sind ersetzt durch eine Schneckenfeder, die mit einem Ende an der Drehachse der Scheibe und mit dem anderen Ende an einem
außen stehenden Fixpunkt befestigt ist. Das rückstellende Drehmoment nach Verdrehen der
Scheibe wird von der Schneckenfeder aufgebracht. Die Scheibe kann damit Drehschwingungen ausführen.
Eindimensionale harmonische Schwingungen
22
A
P
Melast
S
β
0
P’
Abb. 2-08: Torsions- oder Drehpendel – Modell und benutzte Nomenklatur.
A
P − P’
Feder
S
JP
β
β=0
β̂
Melast
Vertikale Achse
Lagerung (reibungsfrei)
Schneckenfeder, die das Rückstellmoment Melast aufbringt
Durchstoßpunkt der Achse durch die Scheibe
Massenträgheitsmoment der Scheibe bezüglich der Drehachse P − P’
(momentaner) Auslenkwinkel des Drehpendels aus der Ruhelage
Ruhelage
Maximaler Auslenkwinkel des Drehpendels
Rückstellmoment der Schneckenfeder (lineares Drehmomentengesetz)
2.3.3.1 Aufstellen der Differentialgleichung
Für kleine Verdrillungen des Aufhängedrahtes findet man experimentell:
Das Rückstell-Drehmoment Melast ist proportional zum Auslenkwinkel β aus der Ruhelage
der Scheibe. Es gilt für den Betrag
Melast = −kt β.
Man nennt die Proportionalitätskonstante kt des linearen Drehmomentengesetzes die Drehfederkonstante (andere Bezeichnungsweisen sind Drehfedersteifigkeit oder Drehfederkoeffizient, alte Formelbuchstaben sind D∗ oder c∗ ). Die Linearität des Betrags des Drehmoments
Eindimensionale harmonische Schwingungen
23
M mit dem Auslenkwinkel β entspricht dem linearen (Hookeschen) Kraftgesetz des FederMasse-Modells mit Felast = −ky.
Ein Drehmoment M bewirkt nach Newton eine Winkelbeschleunigung α gemäß
d2 β
= JS β̈
Analog zum Federpendel mit F = ma = mÿ.
dt2
Man erhält daraus nach Einsetzen des linearen Ausdrucks für Melast die Differentialgleichung
kt
−kt β = JS β̈ oder β̈ +
β = 0.
JS
M = JS α = JS
2.3.3.2 Lösung der Differentialgleichung
kt
β = 0 hat wieder die mathematische Form der DifferenJS
tialgleichung einer ungedämpften harmonischen Schwingung β̈ + ω02 β = 0.
Diese Differentialgleichung β̈ +
In Analogie erhält man sofort die Bewegungsgleichung (Drehwinkel-Zeit-Gesetz)
β(t) = β̂ cos(ω0 t + ϕ0 ),
die Eigenkreisfrequenz
kt
ω02 =
JS
und für die Schwingungsdauer
JS
torsion
= 2π
.
T0
kt
Diese Beziehung für die Schwingungsdauer T0 erlaubt es, Massenträgheitsmomente JP bezüglich einer beliebigen Drehachse experimentell zu bestimmen.
Man ermittelt zunächst die Drehfederkonstante kt , indem man einen homogenen Körper
einfacher Geometrie, dessen Massenträgheitsmoment einfach berechnet werden kann, Drehschwingungen ausführen lässt und die zugehörige Schwingungsdauer T0 misst. Ist damit kt
bekannt, so lässt sich bei Benutzung der gleichen Anordnung das Massenträgheitsmoment
JP eines Körpers beliebiger Geometrie und Massenverteilung durch die Messung der sich
einstellenden Schwingungsdauer T0Körper bestimmen.
2.3.4 Analogien Federpendel – Torsionspendel
Man erkennt folgende, teilweise bereits aus der Mechanik bekannten Zusammenhänge bzw.
Übersetzungsregeln von der Translation des linearen Feder-Masse-Systems auf die Rotation
eines Torsionspendels.
Feder-Masse-System
(Federpendel)
Auslenkung
Masse
Kraft
Federkonstante
Torsionspendel
y
m
F
k
Auslenkwinkel
Massenträgheitsmoment
Drehmoment
Drehfederkonstante
β
JS
M
kt