Aberdeen Glasgow Fort William Edinburgh Perth Inverness 81 120
Werbung
Lösungen zur Prüfung in diskreter Mathematik vom 13. Januar 2009
Aufgabe 1
(a)
� �
n
n(n − 1)
=
2
2
(b)
n·m
(c)
�
(d)
�� � � �
10 9 3 6
2
(−1)5 = 10 · 84 · 6 = −40� 320
1
3
1
�
(e)
�� �
10 8
= 14� 700
6
4
9!
= 22� 680
(2!)4
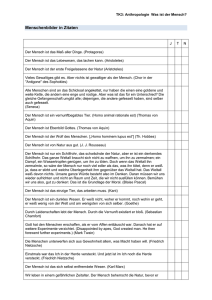
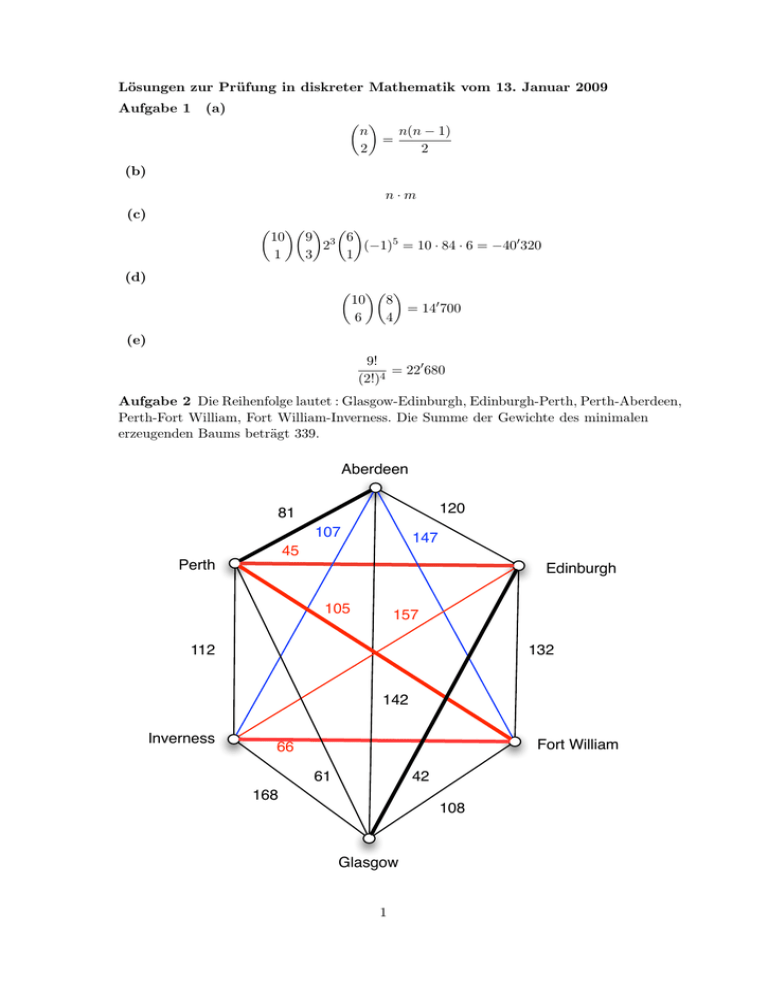
Aufgabe 2 Die Reihenfolge lautet : Glasgow-Edinburgh, Edinburgh-Perth, Perth-Aberdeen,
Perth-Fort William, Fort William-Inverness. Die Summe der Gewichte des minimalen
erzeugenden Baums beträgt 339.
Aberdeen
120
81
107
147
45
Perth
Edinburgh
105
157
112
132
142
Inverness
Fort William
66
61
42
168
108
Glasgow
1
Aufgabe 3 Bestimmen Sie mit dem Algorithmus von Dijkstra die kürzesten Wege
zwischen dem Knoten A und den übrigen Knoten im untenstehenden Graphen.
A
12
20
B
G
14
4
12
8
6
10
C
F
6
6
E
Knoten
L(v)
S
L(v)
S
L(v)
S
L(v)
S
L(v)
S
L(v)
S
L(v)
S
4
D
A B C D E F
0 ∞ ∞ ∞ ∞ ∞
{A}
0 12 ∞ ∞ 14 ∞
{A, B}
0 12 24 22 14 ∞
{A, B, E}
0 12 24 22 14 20
{A, B, E, G}
0 12 24 22 14 20
{A, B, E, G, F }
0 12 24 22 14 20
{A, B, E, G, F, D}
0 12 24 22 14 20
{A, B, E, G, F, D, C}
G
∞
20
20
20
20
20
20
Aufgabe 4 (a) Der erste Graph enthält einen Zyklus. Es ist also kein Baum. Der
zweite Graph ist zusammrnhämgend und enthält keinen Zyklus. Es ist also ein
Baum.
2
3
5
6
1
4
2
1
2
6
3
4
5
(b) Es handelt sich um einen einfachen Graph. Wenn der Graph plättbar wäre, dann
müsste gelten :
a ≤ 3n − 6
��
Es gilt a = 62 = 6·5
2 = 15 und n = 6 . Die Ungleichung ist also nicht erfüllt.
Andere Begründung : Der Graph aus Aufgabe 2 ist der Graph K6 , der den Graph
K5 als Teilgraphen enthält. Da K5 nicht plättbar ist, ist auch K6 nicht plättbar.
(c) Es gilt :
�
δ(v) = 2a
v∈V
Also erhalten wir in unserem Fall :
10 = 2a =⇒ a = 5
Der nachfolgende Graph enthält 4 Kanten. Es ist nicht möglich eine 5-te Kante
zu setzen, ohne den Grad des Knotens 1 zu erhöhen oder einen Graphen mit
Mehrfachkanten zu erzeugen.
3
4
2
1
3
Aufgabe 5 (a) – reflexiv : ja, denn x − x = 0 ∈ Q .
– symmetrisch : ja, denn falls x − y eine rationale Zahl ist, dann ist auch y − x
eine rationale Zahl.
– transitiv : falls x − y eine rationale Zahl ist und y − z ebenfalls eine rationale
Zahl ist, dann ist auch x−z = (x−y)+(y −z) eine rationale Zahl. Die Relation
ist also transitiv.
(b) – reflexiv : nein, denn eine Gerade ist nicht senkrecht zu sich selbst.
– symmetrisch : ja, denn wenn g senkrecht zu h , dann ist h auch senkrecht zu g .
– transitiv : nein. Falls g1 senkrecht auf g2 und g2 senkrecht auf g3 steht, dann
sind g1 und g3 parallel.
(c) – reflexiv : ja, denn zwei identische Seiten haben identische Links.
– symmetrisch : ja, denn wenn die Webseite p1 mit der Webseite p2 einen Link
gemeinsam hat, dann hat die Webseite p2 auch mit p1 einen Link gemeinsam.
– transitiv : nein. Falls p1 mit der Webseite p2 einen Link gemeinsam hat und
p2 mit p3 einen Link gemeinsam hat, dann muss p1 nicht mit p3 einen Link
gemeinsam haben.
4
Solutions de l’épreuve de mathématiques discrètes du 13 janvier 2009
Exercice 1
(a)
� �
n
n(n − 1)
=
2
2
(b)
n·m
(c)
�
(d)
�� � � �
10 9 3 6
2
(−1)5 = 10 · 84 · 6 = −40� 320
1
3
1
�
(e)
�� �
10 8
= 14� 700
6
4
9!
= 22� 680
(2!)4
Exercice 2 L’ordre est donné par : Glasgow-Edinburgh, Edinburgh-Perth, Perth-Aberdeen,
Perth-Fort William, Fort William-Inverness. La somme des poids de l’arbre couvrant
minimal est égale à 339.
Aberdeen
120
81
107
147
45
Perth
Edinburgh
105
157
112
132
142
Inverness
Fort William
66
61
42
168
108
Glasgow
5
Exercice 3 Déterminer avec l’algorithme de Dijkstra le chemin le plus court entre le
noeud A et les autres noeuds dans le graphe ci-dessous.
A
12
20
B
G
14
4
12
8
6
10
C
F
6
6
E
noeuds
L(v)
S
L(v)
S
L(v)
S
L(v)
S
L(v)
S
L(v)
S
L(v)
S
4
D
A B C D E F
0 ∞ ∞ ∞ ∞ ∞
{A}
0 12 ∞ ∞ 14 ∞
{A, B}
0 12 24 22 14 ∞
{A, B, E}
0 12 24 22 14 20
{A, B, E, G}
0 12 24 22 14 20
{A, B, E, G, F }
0 12 24 22 14 20
{A, B, E, G, F, D}
0 12 24 22 14 20
{A, B, E, G, F, D, C}
G
∞
20
20
20
20
20
20
Exercice 4 (a) Le premier graphe contient un cycle. Ce n’est donc pas un arbre. Le
deuxième graphe est connexe et ne contient pas de cycle. C’est donc un arbre.
6
3
5
6
1
4
2
1
2
6
3
4
5
(b) Il s’agit d’un graphe simple. Si le graphe était planaire, il faudrait que
a ≤ 3n − 6
��
On a a = 62 = 6·5
2 = 15 et n = 6 . L’inéquation n’est donc pas satisfaite. Autre
raisonnement : Le graphe de l’exercice 2 est le graphe K6 qui contient le graphe
K5 comme sous-graphe. Puisque K5 n’est pas planaire le graphe K6 n’est pas
planaire non plus.
(c) On a
�
δ(v) = 2a
v∈V
Dans notre cas, on a donc :
10 = 2a =⇒ a = 5
Le graphe ci-dessous a 4 arêtes. Il n’est pas possible de poser une 5e arête sans
augmenter le dregré du noeud 1 ou de créer un graphe avec des arêtes multiples.
7
4
2
1
3
Exercice 5 (a) – réflexive : oui, car x − x = 0 ∈ Q .
– symétrique : oui, car si x − y est un nombre rationnel, y − x est aussi un nombre
rationnel.
– transitive : si x − y est un nombre rationnel et y − z est aussi un nombre
rationnel, alors x − z = (x − y) + (y − z) est aussi un nombre rationnel. La
relation est donc transitive.
(b) – réflexive : non, car une droite n’est pas perpendiculaire à lui-même.
– symétrique : oui, car si g est perpendiculaire à h alors h est aussi perpendiculaire à g .
– transitive : non. Si g1 est perpendiculaire à g2 et g2 perpendiculaire à g3 , alors
g1 et g3 sont parallèles.
(c) – réflexive : oui, car les liens de deux pages web identiques sont identiques.
– symétrique : oui, car si la page web p1 a un lien en commun avec une page p2 ,
la page p2 a aussi un lien en commun avec la page p1 .
– transitive : non. Si p1 a un lien en commun avec p2 et p2 un lien en commun
avec p3 , alors p1 ne doit pas avoir un lien en commun avec la page p3 .
8