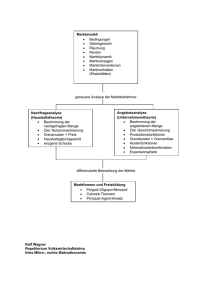
2. Industrieökonomische Grundlagen

Ausgewählte Bereiche der Wirtschaftspolitik
2-1
Prof. Andreas Haufler (WS 2009/10)
2. Industrieökonomische Grundlagen
Definition: Industrieökonomik (industrial organization, IO)
beschäftigt sich mit Auswirkungen von Marktmacht auf das
Verhalten von Firmen
Grundlage: allgemeine mikroökonomische (Preis-) Theorie
bei unterschiedlichen Marktformen (⇒ Kap. 2.1)
Entwicklung eines eigenständigen Fachgebietes in 2 Phasen:
1940-1960: empirische Arbeiten zum Zusammenhang zwischen Marktstruktur, Firmenverhalten und Marktergebnis (Harvard Schule, ⇒ Kap. 1.3, 2.2)
Kritik an theoretischen ad-hoc Annahmen dieser Arbeiten (u.a. durch die Chicago-Schule, vgl. Kap. 1.3)
seit 1970: theoretische Industrieökonomik entsteht durch
Anwendung der (nicht-kooperativen) Spieltheorie
• grundlegendes Lehrbuch: Jean Tirole, The Theory of
Industrial Organization, 1988
• wirtschaftspolitische Anwendung in allen Bereichen
der Wettbewerbs- und Regulierungspolitik
Ausgewählte Bereiche der Wirtschaftspolitik
2-2
Prof. Andreas Haufler (WS 2009/10)
2.1. Grundmodelle der theoretischen IO
(vgl. Weimann 2005, Kap. 7.1)
• Industrieökonomik schließt sowohl monopolistische als
auch oligopolistische Marktformen ein
• zentral für oligopolistische Märkte ist strategische Interaktion zwischen den Firmen
• zwei Grundmodelle: Preiswettbewerb (Bertrand) versus
Mengenwettbewerb (Cournot)
2.1.1 Bertrand Wettbewerb
• hier: homogene Güter
• zwei Firmen i ∈ {1, 2} mit identischen Grenzkosten c
(keine Fixkosten) versorgen den gesamten Markt (Duopol)
• strategische Variable der Firmen ist der Preis (p1, p2)
• gleichzeitige Entscheidungen der Firmen, nicht-kooperatives Spiel
• bei gleichem Preis teilt sich die Nachfrage D(p1, p2)
gleichmäßig auf beide Firmen auf
Ausgewählte Bereiche der Wirtschaftspolitik
2-3
Prof. Andreas Haufler (WS 2009/10)
Nachfragefunktion aus Sicht jeder Firma:








D(pi) wenn pi < pj
Di(pi, pj ) =  D(pi)/2 wenn pi = pj



 0
wenn pi > pj
Gewinnfunktion jeder Firma (keine Fixkosten):
πi = Di(pi, pj )(pi − c)
(2.1)
Nash-Gleichgewicht:
• liegt Preis von Firma i über den Grenzkosten, kann Firma j durch marginales Unterbieten die gesamte Nachfrage auf sich ziehen und Gewinn erhöhen
• ⇒ Preiswettbewerb senkt Preise beider Firmen bis zu
Grenzkosten; p1 = p2 = c als einziges Nash-Gleichgewicht
unerwartetes Ergebnis (Bertrand Paradox); zeigt, dass funktionierender Wettbewerb nicht notwendig viele Firmen voraussetzt
2.1.2 Cournot Wettbewerb
• Annahmen wie unter A., aber strategische Variable ist
jetzt Menge qi und inverse Nachfrage ist p(q1, q2)
Gewinnfunktion jedes Unternehmens:
πi(q1, q2) = p(q1, q2) qi − Ci(qi) ∀ i
(2.2)
Ausgewählte Bereiche der Wirtschaftspolitik
2-4
Prof. Andreas Haufler (WS 2009/10)
Bedingung erster Ordnung:
∂πi
∂Ci
∂p
= p(qi, qj ) −
+ qi
(qi, qj ) = 0
∂qi
∂qi
∂qi
(2.3)
• Differenz der ersten beiden Terme: Zusatzgewinn aus
Mengenausweitung
• dritter Term: inframarginaler Gewinnverlust durch induzierte Preissenkung (abhängig von eigener Marktmacht)
Reaktionsfunktion: jeder Outputentscheidung von Firma j
wird eine optimale (gewinnmaximierende) Reaktion von Firma i, Ri(qj ), zugeordnet. Diese ist implizit definiert durch:



∂πi 


F (qi, qj ) ≡
Ri (qj ), qj  = 0.

|
{z
}
∂qi
qi
(2.4)
Im Cournot-Nash GG ist die Reaktion beider Firmen jeweils
die optimale Antwort auf die Aktion des Konkurrenten:
Ri(qj∗) = qi∗;
Rj (qi∗) = qj∗
(2.5)
Steigung der Reaktionsfunktion aus impliziter Differentiation von (2.4)
∂qi
∂Ri
∂F/∂qj
(∂ 2πi/∂qi ∂qj )
≡
=
=
.
(2.6)
2
2
∂qj
∂qj
−∂F/∂qi
−(∂ πi/∂qi )
bei konkaver Gewinnfunktion gilt ∂ 2πi/∂qi2 < 0 und damit




2
 ∂Ri 
 ∂ πi 




sign 
 = sign 

∂qj
∂qi ∂qj
Ausgewählte Bereiche der Wirtschaftspolitik
2-5
Prof. Andreas Haufler (WS 2009/10)
allgemeine Interpretation: führt eine Erhöhung des Wettbewerbsparameters von Firma j dazu, dass eine Erhöhung des
Wettbewerbsparameters von Firma i profitabler wird?
• ∂Ri/∂qj > 0: (q1, q2) strategische Komplemente
(Bertrand Fall)
• ∂Ri/∂qj < 0: (q1, q2) strategische Substitute
(Cournot Fall)
Abbildung 2.1: Cournot-Nash Gleichgewicht
q2
6
-
Index W : Wettbewerb; M : Monopol
q1
Ausgewählte Bereiche der Wirtschaftspolitik
2-6
Prof. Andreas Haufler (WS 2009/10)
Lerner Index:
aus (2.3) ergibt sich nach Division durch p und Erweitern:
p − C 0 −qi ∂p Q −qi ∂p Q α
L=
=
=
≡
p
p ∂qi Q
Q ∂qi p
ε
(2.7)
• α ≡ qi/Q ist Marktanteil der Firma (Q = q1 + q2 + ...)
• ε = −p/p0Q ist (positiv definierte) Preiselastizität der
Nachfrage
Marktmacht (→ Preis über Grenzkosten) hängt ab von:
1. Marktanteil der Firma
2. Preiselastizität der Nachfrage auf dem Markt
=⇒ im Cournot-Duopol erzielen die Firmen übernormale
Gewinne, die erst mit großer Anzahl der Firmen im Markt
verschwinden [α → 0; vgl. auch (2.3)]
=⇒ qualitativ andere Ergebnisse bei Bertrand und bei Cournot Wettbewerb
Ausgewählte Bereiche der Wirtschaftspolitik
2-7
Prof. Andreas Haufler (WS 2009/10)
Cournot oder Bertrand Wettbewerb?
• keine generelle Antwort in der Industrieökonomie, aber
stärkere Verbreitung des Cournot Modells
• partielle Rechtfertigung der Wahl des Cournot Modells
durch Kreps/Scheinkmann (1983): zweistufiges Spiel mit
Kapazitätsentscheidungen beider Firmen in der ersten
Stufe und Preisentscheidung in der zweiten führt zu den
gleichen Ergebnissen wie das einstufige Cournot Modell
• gewisse Plausibilität des Ergebnisses: Kapazitätsentscheidungen sind ‘langfristiger’ als Preisentscheidungen; können
im Vorfeld zur Abmilderung des Preiswettbewerbs eingesetzt werden (Kapazitäten zu gering, um die gesamte
Nachfrage beim Grenzkostenpreis zu bedienen)
• ähnliche Effekte durch Produktdifferenzierung: Firmen
wählen in erster Stufe differenzierte Produkte, um nachfolgenden Preiswettbewerb abzuschwächen
Ausgewählte Bereiche der Wirtschaftspolitik
2-8
Prof. Andreas Haufler (WS 2009/10)
2.1.3 Bestreitbare Märkte
(vgl. Weimann, Kap. 7.2.4-7.2.5; Knieps, Kap. 2.2)
zentrale Referenz: Baumol, Panzar, Willig (1982): in einem
bestreitbaren Markt (=Markt ohne Eintrittsbarrieren) wird
die Marktmacht auch durch potenziellen Wettbewerb beschränkt
• von n Firmen seien m in einem Markt aktiv und (n−m)
seien potenzielle Wettbewerber
• Marktkonfiguration: Preis und Produktionsmenge für alle im Markt aktiven Firmen
• ein perfekt bestreitbarer Markt liegt vor, wenn beide der
folgenden Bedingungen erfüllt sind:
1. kein aktives Unternehmen macht Verluste und der
Markt ist geräumt
[die Marktkonfiguration ist erreichbar (feasible)]
2. kein potenzieller Wettbewerber kann durch Markteintritt Gewinne machen
[die Marktkonfiguration ist sustainable]
Beispiel: monoton fallende Durchschnittskosten
→ Abbildung 2.2
Ausgewählte Bereiche der Wirtschaftspolitik
2-9
Prof. Andreas Haufler (WS 2009/10)
Abbildung 2.2: Bestreitbarer Monopolmarkt
p
6
-
x
• p < p1 führt zu Verlusten ⇒ nicht feasible
• p > p1 führt zu Markteintritt ⇒ nicht sustainable
• =⇒ ein Anbieter mit p = p1 ist die einzige Konfiguration, die sustainable ist: ein zweiter Anbieter kann wegen
Größenvorteilen nicht eintreten
• keine Gewinne und technologische Effizienz durch Ausnutzung der Fixkostendegression ⇒ Gleichgewicht ist
second-best effizient: Planer, der keine Subventionen
verwenden darf, würde die gleiche Allokation wählen
=⇒ Generalisierung der Ergebnisse des Bertrand Wettbewerbes: Ineffizienz von Monopolen wird auf offenen Märkten
zumindest entschärft (→ Chicago School, 1.3)
Ausgewählte Bereiche der Wirtschaftspolitik
2-10
Prof. Andreas Haufler (WS 2009/10)
Einschränkungen:
1. Theorie bestreitbarer Märkte setzt voraus, dass potenzielle Konkurrenten eine hit-and-run Strategie verfolgen
können. D.h. sie können in den Markt eintreten, produzieren und verkaufen und sofort wieder austreten, bevor
der incumbent reagieren kann.
Aber: der incumbent kann glaubhaft mit Preisen unterhalb der Durchschnittskosten drohen, da seine Fixkosten
bereits versunken sind. Dies schreckt potenzielle entrants ab, wenn sie nicht bei hohen (Monopol-) preisen
in den Markt eintreten und Gewinne machen können,
bevor der incumbent die Preise senkt
2. ist eine hit-and-run Strategie nicht möglich, setzt die
Theorie voraus, dass Fixkosten reversibel sind, d.h. alle
Investitionen können beim Marktaustritt ohne Verlust
verkauft werden (z.B. Fuhrpark).
Liegen irreversible Kosten (sunk costs) vor (z.B. firmenspezifisches Kapital, Werbung für brand name), kann
der incumbent durch die Drohung mit Preisen unterhalb der Durchschnittskosten jeden Wettbewerber vom
Markteintritt abschrecken
=⇒ wirtschaftspolitische Problembereiche dort, wo Größenvorteile und irreversible Investitionskosten auftreten.
Hier ist Regulierung notwendig (Kap. 5 + 6)
Ausgewählte Bereiche der Wirtschaftspolitik
2-11
Prof. Andreas Haufler (WS 2009/10)
2.2 Grundlagen der empirischen IO
(vgl. Knieps, Kap. 3)
• im Mittelpunkt: Erläuterung des Struktur-Verhalten-Ergebnis Ansatzes (structure-conduct-performance paradigm)
der Harvard Schule (Kap. 1.3)
• von sinnvoller Abgrenzung des relevanten Marktes mittels Kreuzpreiselastizitäten wird im Folgenden ausgegangen
2.2.1 Maße für Marktkonzentration und Marktergebnis
Maße für Marktkonzentration:
1. Marktanteil (concentration ratio; CR)
• Umsatz der 1, 4, 8 größten Anbieter auf einem Markt
am Gesamtumsatz des Marktes (CR1, CR4, CR8)
• Problem: kein klares Kriterium, welches Untermaß (CR1,
CR4, CR8) ausgewählt werden soll
2. Herfindahl-Hirschman Index
• Berechnung nach Formel H = Pni=1 s2i
n = Zahl der Anbieter; si= Marktanteil von Anbieter i
(Umsatz von Firma i als Anteil am Gesamtumsatz)
Ausgewählte Bereiche der Wirtschaftspolitik
2-12
Prof. Andreas Haufler (WS 2009/10)
• Wert für Monopol (n = 1): H = 1; Duopol (n = 2):
H = 1/4 + 1/4 = 1/2; Triopol (n = 3): H = 1/3
• bei gleichen Unternehmensgrößen sinkt H mit Zahl der
Unternehmen; für gegebene Unternehmenszahl steigt H
mit steigender Asymmetrie der Firmen; sehr kleine Firmen erhalten (fast) kein Gewicht
• große Rolle bei Fusionsgenehmigungen in den USA
(→ Kap. 4.2)
Maße für das Marktergebnis:
1. Ertrag auf das eingesetzte Kapital (rate of return)
• ökonomischer Gewinn: Π = R − wL − (r + δ)K
mit R= Erlös; wL= Lohnkosten; r= Kapitalrendite; δ=
Abschreibungsrate; K= gesamtes eingesetztes Kapital
• Π = 0 setzen und auflösen nach r ergibt
r=
R − wL − δK
K
(2.8)
2. Preis-Kosten-Spanne
• relativer Aufschlag auf die Grenzkosten (mark-up):
(p − C 0)/p
Ausgewählte Bereiche der Wirtschaftspolitik
2-13
Prof. Andreas Haufler (WS 2009/10)
• entspricht dem Lerner Index (Lerner, 1934) aus Kap.
2.1;
Index ist 1/ε im Monopol und 0 bei vollk. Konkurrenz
3. Tobin’s ‘q’
• Definition: q = M
V mit M : Marktwert des Vermögens
und V : Wiederbeschaffungswert des Vermögens
• q > 1 als Maß für ökonomische Gewinne
• Wiederbeschaffungswert V schwer zu ermitteln → Maß
wird selten verwendet
2.2.2 Der Struktur-Verhalten-Ergebnis Ansatz
• Annahme eines kausalen Zusammenhanges zwischen Marktstruktur (Konzentration), Preissetzungsverhalten und ökonomischem Gewinn
• klassischer Aufsatz von Bain (1951): deutlich höhere rate of return, wenn das Konzentrationsmaß CR8 > 0.7
ist (Durchschnittswerte: 11.8% vs. 7.5%)
**** Tabelle 2.1 *****
Ausgewählte Bereiche der Wirtschaftspolitik
2-14
Prof. Andreas Haufler (WS 2009/10)
Tabelle 2.1 Konzentrationsmaß und Ertragsrate
(Bain, 1951)
Industry
Cigarettes
Typewriters
Motor vehicles
Rubber tires
Tin cans, tinware
Aluminium products
Soap
Washing machines
aircraft and parts
Liquors, distilled
Carpets, rugs
Meat packing
Petroleum refining
Cigars
Cement
Boots and shoes
Paper goods
Confectionery
Lumber, timber products
CR8
99.4
99.3
94.2
90.4
85.6
83.7
83.1
79.7
72.8
71.4
68.2
63.5
58.9
50.7
44.7
30.8
23.7
19.9
7.6
π (∗)
14.4
15.8
16.3
8.2
9.1
9.7
15.2
14.0
20.8
14.2
4.7
3.6
6.8
6.9
5.4
7.5
12.4
16.0
9.1
(*) average ratio of profits/net worth, 1936-1940
Ausgewählte Bereiche der Wirtschaftspolitik
2-15
Prof. Andreas Haufler (WS 2009/10)
Abbildung 2.3: Scatter Plot von Bain’s Analyse
π
6
25
s
20
15
s
((((
s
10
5
s
s
s
(
(
(
s
(
(
s
s
((((
((((
((
((
s
(((
(((
(
(
s
(((
(((
((((
s
ss
s
s
s
s
s
-
0.2
0.4
0.6
0.8
1.0
CR8
Tabelle 2.2: Regressionsanalyse
CR8 > 0.7
Konstante
dummy
(1)
6.219
(3.12)
(2)
7.452
4.386
(7.99)
(3.32)
CR8
0.052
(1.84)
R2
0.078
0.217
(t-Werte in Klammern)
Quelle für Tabelle 2.1-2.2 und Abb.2.3: Martin (2001): Advanced Industrial Economics, 2nd. ed., pp. 124-125
Ausgewählte Bereiche der Wirtschaftspolitik
2-16
Prof. Andreas Haufler (WS 2009/10)
Neuere Arbeiten:
Überblick: Schmalensee (1989) in Handbook of Industrial
Organization oder Martin (2001): Advanced Industrial Economics, 2nd. ed., Ch. 5-7
• in nachfolgenden Arbeiten wird nur ein schwacher und
instabiler Zusammenhang zwischen Konzentrationsmaßen und rate of return ermittelt
• im Zeitablauf starke Schwankungen der sektoralen rate
of return mit Tendenz zum intertemporalen Ausgleich
(Marktein- und -austritte)
• empirische und theoretische Kritik an exogener Marktstruktur führt zu theoretischen Neuansätzen in der Industrieökonomik, die Marktstruktur endogenisieren und
simultan mit Verhalten und Ergebnis bestimmen
• in der Zukunft: stärkere Verknüpfung von neuen theoretischen Ansätzen und empirischer Arbeit
=⇒ Unsicherheit für die Wettbewerbspolitik: ein direkter
und systematischer Schluss von (hohen) Konzentrationsmaßen in einer Industrie auf die Gewinnspanne ist nicht möglich