Ernährung - pharma4u

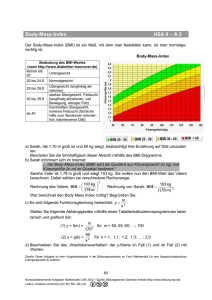
Ernährung
Ernährung
86
3.1 Energie-Einheiten
kJ
= 4,184 · kcal
kcal = 0,24 · kJ
Die Kalorie war lange Zeit die gemeinsame Einheit aller Energieformen,
wie etwa für chemische, elektrische oder kinetische Energie. Sie ist definiert als die Wärmeenergie, die 1 Gramm Wasser bei normalem Atmosphärendruck zugeführt werden muss, um dessen Temperatur von 14,5 auf
15,5 °C zu erhöhen. Da die Anwendung der Kalorie als Einheit wegen der
Abhängigkeit der spezifischen Wärme des Wassers von Druck und Temperatur problematisch ist, wird Energie heute durch Umrechnung in Joule
definiert. Das Joule ist die abgeleitete gemeinsame SI-Einheit für Energie,
Arbeit und Wärme.
Für die Umrechnung gilt:
1 cal = 4,184 J bzw. 1 Joule = 0,239 cal.
Grundumsatz
Altersgruppe
Formel für die Voraussage des Grundumsatzes (GU)
nach WHO, 1985
Frauen
10–18 Jahre
19–30 Jahre
31–60 Jahre
Über 60 Jahre
GU = 0,056 · kg KG + 2,898
GU = 0,062 · kg KG + 2,036
GU = 0,034 · kg KG + 3,538
GU = 0,038 · kg KG + 2,755
Männer
10–18 Jahre
19–30 Jahre
31–60 Jahre
Über 60 Jahre
GU = 0,074 · kg KG + 2,754
GU = 0,063 · kg KG + 2,896
GU = 0,048 · kg KG + 3,653
GU = 0,049 · kg KG + 2,459
Der Energiebedarf des Menschen lässt sich in drei wesentliche Komponenten unterteilen:
– Grundumsatz,
– Umsatz für körperliche Aktivität und
– die Energie für die nahrungsinduzierte Thermogenese.
Der Grundumsatz ist der Energieverbrauch einer gesunden Person in Ruhe, morgens vor dem Aufstehen, nach mindestens 12-stündiger Nahrungskarenz in einer thermoneutralen Umgebung. Er entspricht dem Energiebedarf für die Aufrechterhaltung aller lebenswichtigen Prozesse.
Beim Erwachsenen mit leichter körperlicher Arbeit macht der Grundumsatz mit 50–60 % den größten Teil des täglichen Energiebedarfs aus.
Energie-Einheiten
87
8–12 % werden für die postprandiale Thermogenese, 30–40 % für körperliche Aktivität benötigt. Dazu kommen maximal 10 % für weitere Faktoren,
wie z.B. Thermoregulation.
Der Grundumsatz kann mittels indirekter Kalorimetrie über die Bestimmung des Sauerstoffverbrauchs und der Kohlendioxidproduktion relativ
genau erfasst werden. Einfacher und für die Praxis ausreichend genau
lässt sich der Grundumsatz mit statistischer Sicherheit mittels prädiktiver
Formeln ermitteln. Sehr häufig werden dazu die von der WHO empfohlenen Formeln benutzt (s.o.).
Die Berechnung ergibt den Grundumsatz in MJ/Tag. Durch Multiplikation
mit 239 erhält man den Grundumsatz in kcal/Tag.
Der Grundumsatz ist keine konstante Größe, sondern unterliegt individuellen Schwankungen. So wird er beispielsweise durch den Schlafrhythmus
oder die Außentemperatur beeinflusst.
Der Energieverbrauch des Körpers ist in erster Linie von der fettfreien
Körpermasse abhängig. Da Frauen einen höheren Anteil an Fettgewebe
haben, ist ihr Grundumsatz generell um etwa 10 % niedriger anzusetzen
als der von Männern. Im Übrigen hat auch die genetische Veranlagung einen Einfluss auf die Höhe des Grundumsatzes.
Mit zunehmendem Alter kommt es durch eine Reduzierung des stoffwechselaktiven Gewebes (v.a. Muskelgewebe) zu einer Verminderung des
Grundumsatzes.
Übungsaufgaben: Errechnen des Grundumsatzes
Errechnen Sie den Grundumsatz folgender Patienten:
3.1.1
3.1.2
3.1.3
Marta Meier, Körpergröße 158 cm, Gewicht 70 kg, 69 Jahre.
Karl Schmidt, Körpergröße 180 cm, Gewicht 81 kg, 41 Jahre.
Susanne Zack, Körpergröße 162 cm, Gewicht 47 kg, 22 Jahre.
Ernährung
88
3.2 Energiebedarf bei körperlicher Aktivität
Gesamtenergieumsatz = PAL · Grundumsatz
Ein erheblicher Teil des Energieumsatzes beruht auf dem Energiebedarf
für körperliche Aktivität. Somit hat die Art der beruflichen Beschäftigung
ebenso wie das Freizeitverhalten einen bedeutenden Einfluss auf den täglichen Energiebedarf.
Mithilfe der so genannten PAL-Werte (= physical acitivity level) lässt sich
der durchschnittliche tägliche Energiebedarf eines Erwachsenen in Abhängigkeit von seiner körperlichen Aktivität leicht als Mehrfaches des
Grundumsatzes errechnen. Unter hierzulande üblichen Lebensbedingungen kann der PAL-Wert zwischen 1,2 und 2,4 variieren. Durch den Bezug
auf den Grundumsatz werden auch Faktoren wie Körpergewicht, Alter
und Geschlecht berücksichtigt. Dadurch wird der Energieaufwand für definierte körperliche Aktivitäten auch bei unterschiedlichen Personen vergleichbar.
Für Heranwachsende kann der tägliche Energiebedarf mit der o.g. Formel
nicht berechnet werden, da zusätzliche Energie für den Aufbau der Körpermasse benötigt wird.
Tab.: PAL-Werte zur Berechnung des durchschnittlichen täglichen Energieumsatzes bei unterschiedlichen körperlichen Aktivitäten
PAL*
Körperliche Aktivität
Beispiele
1,2
Ausschließlich sitzende oder
Alte, gebrechliche Menschen
liegende Lebensweise
1,4–1,5 Ausschließlich sitzende Tätigkeit Büroangestellte,
Feinmechaniker
1,6–1,7 Sitzende Tätigkeit, zeitweilig
Laboranten, Kraftfahrer,
zusätzlicher Energiebedarf
Fließbandarbeiter
für gehende und stehende
Tätigkeiten
1,8–1,9 Überwiegend gehende und
Hausfrauen,Verkäufer,
stehende Tätigkeit
Handwerker, Kellner,
Apotheker
2,0–2,4 Körperlich anstrengende
Bauarbeiter, Landwirte,
berufliche Arbeit
Waldarbeiter, Bergarbeiter,
Leistungssportler
* Für sportliche Betätigungen oder für anstrengende Freizeitaktivitäten (30–60 Minuten, 4bis 5-mal pro Woche) können zusätzlich pro Tag 0,3 PAL-Einheiten zugelegt werden.
Energiebedarf bei körperlicher Aktivität
89
Übungsaufgaben: Errechnen des Energieumsatzes
Berechnen Sie den durchschnittlichen täglichen Energieumsatz für die Ihnen bereits bekannten Patienten aus dem Kapitel »Grundumsatz«. Sie gehen folgenden Berufen nach:
3.2.1
3.2.2
3.2.3
Marta Meier: Hausfrau.
Karl Schmidt: Sachbearbeiter.
Susanne Zack: Laborantin.
Ernährung
90
3.3 Beurteilung des Körpergewichts nach Broca
Normalgewicht nach Broca:
Körperlänge (cm) – 100
Körpergewicht (kg)
Broca-Index = ––––––––––––––––––––––––––––––––
Broca-Normalgewicht (kg)
Nach statistischen Untersuchungen einer amerikanischen Versicherungsgesellschaft ist das »Normalgewicht nach Broca« das Gewicht mit dem geringsten Risiko zu erkranken oder vorzeitig zu sterben.
Der Broca-Index als Quotient aus dem gemessenen Körpergewicht und
dem errechneten Broca-Normalgewicht gibt eine Aussage über den Grad
der Abweichung vom Sollgewicht. Er wird häufig in Prozent angegeben
(multipliziert mit 100). Eine Adipositas besteht dann, wenn das Ist-Gewicht um mehr als 20 % über dem Soll-Gewicht liegt.
Das früher populäre »Idealgewicht nach Broca« (Normalgewicht abzüglich
10–15 %) basierte auf z. T. fehlerhaften Untersuchungen. Es wird heute
nicht mehr empfohlen, da es zu niedrig und damit für die Gesundheit unvorteilhaft ist.
Beurteilung des Körpergewichts nach Broca
91
Übungsaufgaben: Errechnen des Normalgewichts
Errechnen Sie das Normalgewicht sowie den Broca-Index für folgende Patienten:
3.3.1
3.3.2
3.3.3
Marta Meier, Körpergröße 158 cm, Gewicht 70 kg.
Karl Schmidt, Körpergröße 180 cm, Gewicht 81 kg.
Peter Müller, Körpergröße 184 cm, Gewicht 92 kg.
Ernährung
92
3.4 Beurteilung des Körpergewichts
mit dem Body Mass Index (BMI)
Körpergewicht (kg)
BMI= ––––––––––––––––––––––––––––––––––––––––––
Körpergröße (m) · Körpergröße (m)
Der BMI gilt heute als Standard zur Beurteilung des Körpergewichts. Er
ist definiert als Quotient des Körpergewichts (kg) und dem Quadrat der
Körpergröße (m2).
Von den verschiedenen Gewichtsgrößen-Indizes korreliert der BMI am
besten mit der Körperfettmasse. Allerdings ist im Einzelfall zu berücksichtigen, dass ein hohes Körpergewicht auch z.B. aus großer Muskelmasse
oder extrazellulärem Wasser (Ödeme) resultieren kann. So haben BodyBuilder oder Leistungssportler oft einen hohen BMI bei gleichzeitig niedriger Körperfettmasse.
Bei Kindern und Jugendlichen hat sich die Verwendung des BMI bis heute
nicht etabliert. Zur Beurteilung des Ernährungszustands werden hier
stattdessen weiterhin die Wachstums- und Gewichtskurven in Perzentilen
angewandt.
Der Ernährungszustand wird anhand des BMI allgemein wie folgt beurteilt:
BMI
Beurteilung
< 18,5
18,5–24,9
25 –29,9
Untergewicht
Normalgewicht
Leichtes Übergewicht: Bei Vorliegen weiterer Risikofaktoren wird Gewichtsreduktion empfohlen
Adipositas: Gewichtsreduktion empfohlen
≥ 30
Statistische Untersuchungen haben ergeben, dass ein BMI > 30 bzw. < 18,5
kg/m2 mit einer erhöhten Mortalität einhergeht. In Abhängigkeit vom Alter werden folgende BMI-Bereiche hinsichtlich der Gesundheit als wünschenswert beurteilt:
19–24 Jahre
25–34 Jahre
35–44 Jahre
45–54 Jahre
55–64 Jahre
über 64 Jahre
19–24
20–25
21–26
22–27
23–28
24–29
Beurteilung des Körpergewichts mit dem Body Mass Index (BMI)
93
Übungsaufgaben: Errechnen des BMI
3.4.1
3.4.2
3.4.3
3.4.4
Errechnen Sie Ihren eigenen BMI.
Errechnen Sie den BMI folgender Patienten und beurteilen Sie das
Körpergewicht unter gesundheitlichen Aspekten:
Marta Meier, Körpergröße 158 cm, Gewicht 70 kg, 69 Jahre,
Karl Schmidt, Körpergröße 180 cm, Gewicht 81 kg, 41 Jahre,
Susanne Zack, Körpergröße 162 cm, Gewicht 47 kg, 20 Jahre.
Wie viel Kilo muss Frau Zack mindestens zunehmen, um Normalgewicht zu erlangen?
Errechnen Sie für Ihre eigene Körpergröße und Ihr Alter den gesundheitlich empfehlenswerten Gewichtsbereich.
Ernährung
94
3.5 Fettverteilung
Taillenumfang (cm)
Waist-Hip-Ratio (WHR) = ––––––––––––––––––––––––
Hüftumfang (cm)
Der Quotient aus Taillen- und Hüftumfang ist ein häufig genutztes anthropometrisches Maß zur Beurteilung der Fettverteilung. Als Begriff hat sich
die englische Bezeichnung Waist-Hip-Ratio eingebürgert.
Übergewichtige Männer weisen in der Regel ein androides oder abdominelles Fettverteilungsmuster auf, d.h. der Taillenumfang (Abdominalfett)
übertrifft den Hüftumfang. Bei Frauen ist es meist umgekehrt. Doch gibt es
auch Frauen mit androider bzw. auch Männer mit gynoider Fettverteilung.
Abdominell abgelagertes Fett geht mit einem höheren Risiko kardiovaskulärer Folgeerkrankungen einher als Fett im Hüftbereich. Somit ist also
nicht nur das Ausmaß des Übergewichts, sondern auch die Verteilung der
Fettdepots für die Bewertung des Körpergewichts bedeutsam. Bei nur
mäßigem Übergewicht ist die WHR ein Entscheidungskriterium für die
Frage, ob eine Gewichtsreduktion notwendig ist.
Die Waist-Hip-Ratio sollte bei Männern unter 1,0 und bei Frauen unter
0,85 liegen, darüber liegende Werte gehen mit einem deutlich erhöhten Risiko für Folgeerkrankungen einher.
Neuerdings wird auch der Taillenumfang allein für die Risiko-Bewertung
von Übergewicht herangezogen. Ein Taillenumfang von mehr als 102 cm
bei Männern bzw. von mehr als 88 cm bei Frauen wird als deutlich erhöhtes Krankheitsrisiko angesehen.
Fettverteilung
95
Übungsaufgabe
3.5.1
Ermitteln Sie Ihre eigene Waist-Hip-Ratio.
Ernährung
96
3.6 Nährstoffdichte
Nährstoffgehalt(µg/mg/g pro 100 g Lebensmittel)
Nährstoffdichte
[µg/mg/g pro MJ] = –––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Brennwert (MJ pro 100 g Lebensmittel)
Die Nährstoffdichte beurteilt ein Lebensmittel als Nährstofflieferant. Dabei wird der Nährstoffgehalt in Beziehung zum Energiegehalt des Lebensmittels gesetzt: die Nährstoffdichte ist definiert als Quotient von Nährstoffgehalt und Brennwert eines Lebensmittel. Je höher die Nährstoffdichte ist,
desto günstiger ist das Verhältnis zwischen Nährstoff- und Energiegehalt.
Es ist zu beachten, dass die Zubereitung eines Lebensmittels dessen Nährstoffdichte verändern kann: etwa wenn der Energiegehalt steigt (z.B. beim
Frittieren) oder der Gehalt eines Nährstoffs abnimmt (z.B. Verlust von Kalium im Kochwasser).
Die Kenntnis der Nährstoffdichte ist wichtig, wenn eine energiebegrenzte
aber nährstoffreiche Ernährung erforderlich ist. Alte Menschen beispielsweise benötigen eine Ernährung mit überdurchschnittlich hoher Nährstoffdichte, da der Energieumsatz im Alter sinkt, der Bedarf an Protein,
Mineralstoffen, Vitaminen und Spurenelementen jedoch unverändert
bleibt.
Die Nährstoffdichte lässt sich auch für die gemischte Kost eines Tages berechnen. So wird jeweils die Summe der Nährstoffgehalte durch die Summe der Brennwerte der verzehrten Portionen dividiert. Anhand der DGEEmpfehlungen der Nährstoffdichten für die verschiedenen Bevölkerungsgruppen ist eine Beurteilung des Versorgungszustands eines Menschen
möglich.
Obst und Gemüse weisen aufgrund ihres hohen Vitamin- und Mineralstoffgehaltes und ihres geringen Energiegehaltes die höchsten Nährstoffdichten
auf. Auch fettarme Milch(produkte) sowie mageres Fleisch und Fisch verfügen über hohe Nährstoffdichten.
Beispiel 1: Die Nährstoffdichte verschiedener Obstsorten
Die Banane ist als besonders kaliumreiches Obst bekannt. Gleichzeitig ist
sie aber auch sehr energiereich. Bezogen auf die Nährstoffdichte schneiden
andere Obstsorten wie z.B. Erdbeeren ebenso gut ab.
Obst
Kalium
(mg je 100 g)
Energie
(MJ je 100 g)
Nährstoffdichte für
Kalium (mg/MJ)
Banane
Erdbeere
382
147
0,392
0,134
974
1 097
Nährstoffdichte
97
Übungsaufgaben: Errechnung der Nährstoffdichte
3.6.1
Errechnen Sie die Nährstoffdichte der unten genannten Lebensmittel für die angegebenen Nährstoffe:
Lebensmittel
Trinkmilch 3,5% Fett
Trinkmilch 1,5% Fett
Buttermilch
Lebensmittel
Kalbsschnitzel
Schweineschnitzel
Hinterschinken
Calcium
(mg je 100 g)
120
123
109
Vitamin B1
(mg je 100 g)
0,18
0,80
0,80
Energie
(MJ je 100 g)
Nährstoffdichte für
Calcium (mg/MJ)
0,267
0,195
0,144
Energie
(MJ je 100 g)
0,414
0,443
1,145
Nährstoffdichte für
Vitamin B1
(mg/MJ)
Ernährung
98
Literaturquellen
Biesalski, Hans Konrad u.a. (Hrsg.): Ernährungsmedizin. Stuttgart, New York
1999
Biesalski, Hans Konrad; Grimm, Peter: Taschenatlas der Ernährung. Stuttgart,
New York 1999
Deutsche Gesellschaft für Ernährung (DGE): Referenzwerte für die Nährstoffzufuhr. Frankfurt am Main 2000
Elmadfa, Ibrahim; Fritzsche, Doris: Die große GU Vitamin und Mineralstoff
Tabelle. München 1998
Müller, Manfred J.: Ernährungsmedizinische Praxis: Methoden – Prävention –
Behandlung. Berlin, Heidelberg 1998
Paul-Prößler, Ute: Was heißt Nährstoffdichte? Aus : wichtige Fragen – richtige
Antworten, CMA Centrale Marketing-Gesellschaft der deutschen Agrarwirtschaft mbH (Hrsg.), 1998
Schauder, Peter; Ollenschläger Günter: Ernährungsmedizin: Prävention und
Therapie. München, Jena 1999
Suter, Paolo M.: Checkliste Ernährung. Stuttgart, New York 2002