5. Elektrische Eigenschaften

5. Elektrische Eigenschaften
5.1 Leitfähigkeit von Polymeren
Polymere sind meistens gute Isolatoren!
Leitfähigkeit setzt eine Beweglichkeit der Elektronen voraus (entlang der Kette
und von einer Kette zur nächsten)
Vergleich der Leitfähigkeiten:
Teflon (PTFE)
Polyacetylen, undotiert
Silber, Kupfer
10-16 S/m
10-10 S/m
108 S/m
Polyacetylen
schon bei Raumtemperatur geringe Leitfähigkeit
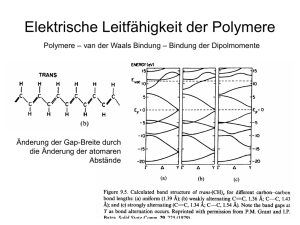
Grund: Peierls Übergang (Theorem: 1-dim Metalle sind instabil durch die
Bildung einer Energielücke am Fermi-Niveau)
trans-Struktur des Polyacetylen = 2-fach entarteter Grundzustand A und B
Einzel- und Doppelbindungen können ohne Energieänderung austauschen
Bildung von freien-Radikalen wo Zustand A und B zusammentreffen (dieser
Defekt wird neutrales Soliton genannt)
stabil: Ladung des freien Elektrons wird über alle Monomereinheiten verteilt
1
5.2 Photoleitfähige Polymere
In Isolatoren kann durch Lichteinstrahlung ein Strom in einem elektrischen Feld
erzeugt werden. Lichteinstrahlung produziert also freie Ladungsträger.
Historisches
Beispiel
NaCl
mit
Farbzentren: NaCl-Kristallen die 1016
Farbzentren/cm³ enthalten. Bei höheren
Temperaturen treten höhere Dunkelströme
auf. Photoströme können nach Anregung
mit Blaulicht durch Rotlicht wieder
reaktiviert werden.
• Elektronen, die lose an eine Anionenleerstelle gebunden sind, absorbieren
Licht
• Lose gebundenes Elektron wird ins Leitungsband angeregt
• Dort bewegt es sich so lange bis es wieder eingefangen wird
• Gemessener Strom entspricht der Verschiebung der Elektronen im
elektrischen Feld.
Beispiele für photoleitfähige Polymere:
a) Poly-N-vinyl-carbazol (PVK)
Polymer mit Seitengruppen
Schematische Darstellung eines Ladungsträgers (Lochzustand)
In PVK ist das Elektron-Loch Paar an einer Carbazol-Einheit lokalisiert.
Polymer-Rückgrat trägt nicht zur Leitung bei.
Loch-Zustand ist ein Radikalkation: Elektronen eingebunden, Löcher sind
beweglich
typische effektive Beweglichkeiten
μ = 10-6 cm²/Vs
2
b) Polysilan
quasikonjugierte Polymere
Schematische Darstellung eines Ladungsträgers (Lochzustand)
konjugierte Polymere (= eine Einfachbindung zwischen zwei Doppelbindungen): Photoleitfähigkeit auch längst der Polymerhauptkette
typische effektive Beweglichkeiten
μ = 1 cm²/Vs
Anwendungen:
• Antistatische Beschichtungen für photografische Filme
• Strahlungsschutz an Computerbildschirmen
• Selbsttönende Fenster, die im Sommer das Sonnenlicht abfangen
Hier: Bandlücke im UV-Bereich.
Die Fallen sind jedoch flach, so daß IR Licht genügt, um Elektronen wieder zu
reaktivieren.
Farbzentren sind nicht nur Quellen freier Elektronen sondern auch effiziente
Fallen ("traps").
Mechanismus der Photoleitfähigkeit:
Excitonen
• Einfallendes Licht hebt Elektron aus dem Valenzband ins freie Leitungsband:
Schaffung eines Elektron-Loch Paares
• Schwingungsanregung dieses Zustandes ≡ Exciton
• Wegen van-der-Waals WW nur geringe Überlappung der Wellenfunktionen
• Starke Lokalisierung der excitonischen Anregung ≡ sogenannte Frenkel
Excitonen
• Gegensatz: Excitonen im Halbleitern sind wegen starker Überlappung der
Elektronen-Wellenfunktionen 3-dim. bis zu 100 Å ausgedehnt (MottWannier Excitonen) ⇒ Ladungsträger sind also über das ganze Gitter
verteilt.
Bewegung der Ladungsträger ist also ein Hüpfprozeß
3
Genauer:
• Ladungsträger-Erzeugung als Folge eines hochangeregten ExcitonenZustandes geschieht im Picosekunden Bereich
• Quantenausbeute wird am stärksten durch Rekombination des Elektron-Loch
Paares auf Grund der eigenen gegenseitigen Coulomb WW reduziert. Diese
Rekombination kann durch Anlegen hoher Felder teilweise unterdrückt
werden. Sind Elektron und Loch aus ihrem gegenseitigen Coulombpotential
befreit, können sie sich frei im elektrischen Feld bewegen.
• Einer der beiden Ladungsträger wird an der dem Licht ausgesetzten
Oberfläche rekombiniert, die andere Ladungsspezies drifted durch Probe
(Folie)v zur Gegenoberfläche. Deren Beweglichkeit μ(cm²/Vs) im elektrostat.
Feld E wird gemessen.
v
v
v = μ⋅E
Driftgeschwindigkeit
• Bandabstand ist im allgemeinen bei ca. 4 eV (für Anwendung sehr hoch)
• Erniedrigung dieses Bandabstandes durch Charge-Transfer WW.
Beispiel: In unmittelbarer Nähe des Donatormoleküls Carbazol wird ein
starker Elektronenakzeptor wie Trinitrolfluorenon (TNF) gebracht. Dies
erniedrigt die Gesamtenergie für Elektron-Loch Paar Erzeugung
hν charge transfer = I donator − I akzeptor −
ΔΕ
{
Coulomabsenkung
Vergleich eines Elektron-Loch-Zustandes in PVK (links)
und eines 'Charge-transfer'-Zustandes im Donator-Akzeptor-Komplex PVKTNF (rechts)
⇒ Resultat: Übergänge werden vom UV-Bereich in den IR-Bereich verschoben
⇒ DOTIERUNG !
4
Anwendung: Elektrophotographie (Xerokopie)
Photoleitende Schichten früher Chalkogenid-Gläser (Se), heute photoleitende Polymere.
a) Gleichförmiges Besprühen der photoleitenden Schicht mit Ladungen durch
Corona-Entladung. Draht in der Nähe der photoleitenden Schicht auf hoher
Spannung bis zur Durchschlagsfeldstärke der Luft.
b) Positiv-Bild wird auf photoleitfähige Schicht projektiert. An hellen Flächen
wird durch Photoleitfähigkeit Ladung abgebaut. Optisches Bild wird in
elektrostatisches Bild umgewandelt.
c) Gegensinnig (hier negativ) geladene Tonerteilchen haften an den geladenen
Stellen.
d) Übertragung der Tonerteilchen auf gegensinnig aufgeladenes Papier.
e) Einschmelzen der Tonerteilchen auf Papieroberfläche durch IR-Bestrahlung
(Toner = leichtschmelzendes organisches Harz)
f) Fertige Kopie des Originalbildes.
Der Laserdrucker basiert auf gleichem Prinzip, lediglich die anfängliche Optik
ist durch abtastenden Laserstrahl ersetzt.
5
Theoretische Beschreibung:
a) Onsager Ansatz zur Beschreibung des Elektron-Loch Trennungsvorgang
f
Uv
E
θ
Trennungswahrscheinlichkeit ∝ φ (Quantenausbeute)
gegenseitiges Coulombpotential
Feldstärke
v
Winkel zwischen Dipolaxe und E
⎡
∂f kT
u ⎤
μ div ⎢e kT grad f ⎥
=
∂t
kT ⎦
e
⎣
u
b) Modelle zur Beschreibung der Beweglichkeit
einfacher Ansatz:
Vangelegte = E ⋅ l und vd = μ ⋅ E
Spannung
l
l2
=
μ ⋅ E Vμ
Sind also l (Schichtdicke des photoleitenden Polymers), V (angelegte Spannung)
bekannt, läßt sich über die Messung von τt die Beweglichkeit μ bestimmen.
⇒ τt =
Die Quantenausbeute φ ist dann proportional der insgesamt abgeflossenen
Ladung
∞
Q = ∫ I (t )dt
0
Typisch für ungeordnete Strukturen ist der Zeitverlauf I(t) durch komplexe
Relaxationsgesetze gekennzeichnet
Beispiel: Polysiloxan
Transientzeit τt aus Lage des
Abknickpunkt
Bereiche konstanter Steigerung in der log I - gegen - log t Kurve legen die
Gültigkeit von Skalengesetzen nahe.
6
Transport im amorphem Körper durch breite Verteilung g(ε) einfachexponentieller Hüpfraten zu beschreiben
ψ(t) = Wahrscheinlichkeit, daß Ladungstäger der zur Zeit t0 = 0 an einem
bestimmten Platz angekommen ist, diesen zur Zeit t wieder verläßt
ψ (t ) = ∑ g (ε )⋅ W (ε )e −W (ε )t
ε
↑
Zustandsdichte
entsprechender
ψ(ε) Beiträge
↑
Hüpfwahrscheinlichkeit
Wichtig: Einfach exponentiell abfallende Hüpfzeitkorrelation ψ(t) = r e-rt
ergibt
konstante Driftgeschwindigkeit vd (t) = const.
Aber: Langzeitverhalten ψ (t ) t →∞ ∝t
für Polymer realistischer.
Modellierung eines solchen Langzeitverhaltens durch Fallenmodell:
• Landungsträger werden mit Wahrscheinlichkeit 1 eingefangen wenn sie an
einer Falle vorbeikommen
• Eingefangene Ladungsträger entkommen durch Boltzmann-Aktivierung den
Fallen
− ε / kT
− (1+α )
W ( ε ) = W0 e
• Zur
↑
Versuchsfrequenz
Vereinfachung exponentielle
g (ε ) = e −ε / kT0
Fallenverteilung
in
Energieraum
• Einsetzen in Gleichung für ψ(t) (siehe vorher) ergibt
ψ (t ) ≈ ∑ e −ε / kT e −ε / kT exp− {W0 te −ε / kT }
0
ε
Mathematisch kann diese Gleichung in
ψ (t ) = ∑ a n b n e − b t
n
umgeschrieben werden
n
Diese Gleichung hat Langzeitverhalten ψ(t) ∝ t-(1+α) mit α = T/T0
Der Exponent n kann physikalisch durch hierachisches Modell erklärt werden
Wij = e
− ΔΕ ij
kT
=e
− nΔ
kT
= b mit b = e
n
−Δ
Beispiele: Polyvenylcarbazol, Polysilan, amorphes Silizium
7
kT
Messung der Photoströme in amorphen Materialien:
← Halbdurchlässige Al-Elektrode
← Phozoleitendes Polymer
← Halbdurchlässige Al-Elektrode
← Polyesterträgerfilm
a) Siloxan-Polymere mit Carbazoleinheiten als
photoleitende Spezies
b) Polysilan-Polymere
c) Amorphes Silizium
Als Konsequenz des Potenzgesetzes für die
Hüpfwahrscheinlichkeit wird die makroskopische
Beweglichkeit μ zeitabhängig.
Dies unterscheidet amorphe Polymere von kristallinen
Photoleitern.
Anschauliche Erklärung dieser
zeitabhängigen Beweglichkeit:
Zunächst Ladungsträgererzeugung; dann
Einfangen in statistisch verteilte Fallen; auf
Grund der Boltzmann-Aktivierung verweilen
Ladungsträger in den tieferen Fallen länger,
dies entspricht einem Abfall des
"Schwerpunkts" der Ladungsträger in tiefere
Fallen mit der Zeit; dies wiederum bedeutet
effektive Verlangsamung der Beweglichkeit.
Deshalb Korrektur der Annahme: (Beispiel: Polysiloxan α = 0.58±0.04)
τt ∝ Ε
τt ∝ l
− 1α
1
α
8
≠ Ε −1
≠l
5.3 Dotierung
1977: A. J. Heeger, A. G. Mac Diarmind, H. Shirakawa: Leitfähigkeit von
dünnen Polyacetylen Filmen um Faktor 109 erhöht durch Dotierung mit
Halogenen (Polyacetylen mit Cl, Br und J bedampft)
⇒ 2000 Nobelpreis für Chemie
Vergleich der Leitfähigkeiten:
Polyacetylen, undotiert
Polyacetylen, dotiert
Silber, Kupfer
10-10 S/m
105 S/m
108 S/m
Leitfähigkeit durch Dotierung:
1) Oxidation:
• analog zu Entfernung von Elektron aus Valenzband (Schaffung von
Akzeptorzustand)
• keine p-Dotierung im eigentlichen Sinne
• durch AsF5, Br2, I2, HclO4
2) Reduktion:
• analog zu Hinzufügung von Elektron ins Leitungsband (Schaffung von
Donorzustand)
• keine n-Dotierung im eigentlichen Sinne
• durch elektrochemische Methoden oder Alkalimetallnaphthalide
Polyacetylen
stabil: freie Ladung wird über alle Monomereinheiten verteilt
hohe Dotierungs-Level: Solitonregionen überlappen
→ Zusammenführung von Valenz- und Leitungsband
→ metallische Leitfähigkeit
9
5.4 Elektroluminiszenz
Seit ca. 1990 sind einige konjugierte Polymere bekannt, die unter Anlegung
einer Spannung Licht ausstrahlen. Hier eröffnet sich prinzipiell die Möglichkeit
großflächige, flexibel, zweidimensional adressierbare und in der Farbe
durchstimmbare LED's herzustellen.
Polymer LEDs
Beispiele für Polymere mit Elektroliminiszenz:
a) Poly-para-phenylen-vinylen (PPV)
Herstellung von PPV über Precursor-Polymer
- Precursor Polymer aus Lösung zu beliebigen mechanischen Formen herstellbar
- Thermische Konvertierung des Precursor-Polymers bei T>250°C
- Degradation ab T>400°C
Schema der Synthese von Poly-para-phenyl-vinylen:
α, α'-dichloro-p-xylene wird polymerisiert zu einem Sulphonium-Salz-Intermediat. Dieses
Präpolymer wird zu Filmen verarbeitet und unter UV-Einstrahlung oder Temperung bei T ≅
320°C und unter Abspaltung von Tetrahydrothiophen und HCl zu dem konjugierten PPV
konvertiert.
10
Eigenschaften von PPV Devices:
← Negative Deckschicht
← PPV Film
← Positiv leitender Kontakt
← Träger
negative Deckschicht:
Al, Mg, Ag-Legierung, a-Si-H, C
→ niedrige Austrittsarbeit, Elektroneninjektor
positiver Kontakt:
Al2O3, Au, InO, InZnO (ITO), Polianilin (PANI)
→ hohe Austrittsarbeit, Lochinjektor
Träger:
Glasplatte oder flexibeles PET (durchsichtig)
1) Strom-Spannungskennlinien haben Schottky-Dioden Charakter
Strom-Spannungs-Charakteristik
für
70nm PPV-Film mit einer aktiven Fläche
von 2mm², positive InO und negative AlElektrode
Kennlinien der Al/PPV/ITO bzw.
Ca/PPV/ITO Dioden sowie die
Intensität der Elektrolumineszenz. Die
aktive Fläche betrug 25mm.²
11
2) Proportional zum Strom Lumineszenz im gelb-grünen Bereich
Elektrolumineszenz (Lichtausbeute) in
Abhängigkeit des Stromes für 70nm
PPV-Film mit einer aktiven Fläche von
2mm², positive InO und negative AlElektrode
3) Spektrale Intensität hängt stark von der Temperatur ab
(heute gute Quantenausbeute (1%) bei RT
Spektrale Intensität der Elektrolumineszenz bei verschiedenen
Temperaturen Stromes für 70nm
PPV-Film mit einer aktiven
Fläche von 2mm², positive InO
und negative Al-Elektrode
4) Durchschaltungspannungen der Diode von anfangs (1990) 14 Volt auf jetzt
(1994) 2-4 Volt abgesenkt
Lumineszenz setzt stets bei Durchbruchspannung an.
Welcher Mechanismus führt zur Lumineszenz ?
a) Strom-Spannungskennlinien können mit der
Halbleiter-Diode beschrieben werden.
Shockley-Gleichung
für
I = I0 (eqV/nkT - 1)
Trotzdem ist Dioden -Ersatzschaltbild noch fraglich.
b) Elektron und Loch werden von den beiden Seiten des Polymers emittiert und
rekombinieren im Inneren. Hierbei Excitonen-Erzeugung, welche durch
Lumineszenz abregen. Der viel häufiger vorkommende Konkurrenzprozess
(99%) ist strahlungslose Rekombination in Fehlstellen
12
b) Poly-para-phenylen (PPP)
kein entarteter Grundzustand, Grundzustand ist die Benzenoidform A
erster angeregter Zustand ist die Quininoidform B mit leicht höherer Energie
also keine Soliton-Defekte die zur Leitfähigkeit führen
Lokalisierte Elektron-Lochpaare polarisieren lokal die Umgebung
Relaxation in neuen Grundzustand: Polaron (Stabilisierung der Quininoidform)
Polaron kann nur durch Überwindung von Energiebarriere bewegt werden
Paar von Polaronen heißt Bipolaron
Bewegung der Ladungsträger ist also ein Hüpfprozeß
13
Eigenschaften von PPP Devices:
Al
PPP
ITO
Glas
•
•
•
•
wird ebenfalls über Precursor-Polymer als Lösung hergestellt
PPP hat ein Band-gap von 2.7 eV,
Filmdicken von 0.5 μm wie bei PPV
großer Unterschied zu PPV:
a) Elektrolumineszenz (und Photolumineszenz) wird ab einer Sperrspannung
±10V beobachtet
b) Betrieb des Devices unter Anlegung einer Wechselspannung
⇒ Beschreibung als Schottky-Diode inadequat.
Lumineszenz wird wie vorher als Strahlungszufall von Excitonen beschrieben.
Besonderheit von PPP: Es leuchtet im blauen Bereich → technisch attraktiv
Anwendungen:
Optoelektronik
Stimulierte Emission → Laserlichtemission nach optischem Pumpen
Beispiel: Poly-phenyl-phenylen-vinylen/PMMA Laser nach optischem Pumpen
und resultierende Interferenzen nach Durchgang durch Michelson Interferrometer (zeigt Kohärenz der Strahlung)
14
Geometrien von optischen Devices, die mit herkömmlichen Feststofflasern nicht
realisierbar sind:
Zukunft:
Verbesserung der Eigenschaften durch Synthese von Polymeren mit einer
geänderten Kettenarchitektur
Lineares PPP
Chirales PPP
oder neuer Polymere
Poly-(3,9-di-t-buthylindeno[1,2b]fluoren) (PIF)
15
5.5 Dielektrisches Verhalten von Polymeren
Polymere sind meistens gute Isolatoren.
Isolator in einen Plattenkondensators ändert die Kapazität gegenüber Vakuum:
Q = Cvac ⋅ Uvac = C⋅U = ε ⋅ Cvac ⋅ U
Bei Stoffen, in denen beim Anlagen eines elektrischen Feldes Dipole durch
Ladungsverschiebung entstehen bzw. vorhandene Dipole durch Polarisation in
Feldrichtung gedreht werden, ist ε größer als εvac = 8.854 x 10-12 A s V-1 m-1
εrel = ε/εvac = relative Dielektrizitätskonstante
Gegen die Ladungsverschiebung bzw. das Ausrichten der Dipole in Feldrichtung
wirken Reibungskräfte. Dadurch entstehen im elektrischen Wechselfeld, d.h.
bei periodischer Bewegung der Ladungen bzw. Dipole, Verluste. Als Folge
dieser dielektrischen Verluste beträgt die Phasenverschiebung zwischen Strom
und Spannung einer realen Kondensatoranordnung bei Speisung mit
Wechselstrom nicht 90° sondern 90°-δ . Dabei ist δ der Verlustwinkel und ist
ein Maß für die Dämpfung oder den Verlust und führt zur Aufheizung.
Messung von ε und tan δ erfolgt mit Brückenschaltung. Der zu untersuchende
Stoff wird in einen Brückenkondensator mit bekannter Abmessung eingebracht.
Zusammenfassung beider Anteile in komplexe Dielektrizitätskonstante
ε(ν) = ε'(ν) – i ε"(ν)
mit tan δ =
ε ′′(ν )
ε ′(ν )
ε'(ν) zeigt Dispersion, Abfall mit steigender Frequenz
ε"(ν) zeigt ein Absorptionsmaximum bei Resonanzfrequenz
Anstatt im Frequenzraum kann Dielektrizitätskonstante auch im Zeitraum durch
Einschalten oder Abschalten eines Feldes und Beobachtung der zeitabhängigen
Größe gemessen werden.
φ (t ) =
ε (t ) − ε ∞
ε = ε bei ν = ∞ bzw. 0
ε 0 − ε ∞ ∞ ,0
Verbindung von Zeit zu Frequenzraum durch Fouriertransformation
∞
ε (ν ) − ε ∞
= 1 − iω ∫ φ (t )e
ε0 − ε∞
0
− iωt
Trennung von Real und Imaginärteil
dt
∞
ε ′(ν ) − ε ∞
= 1 − ω ∫ φ (t ) sin ωtdt
ε0 − ε∞
0
∞
ε ′′(ν )
= ω ∫ φ (t ) cos ωtdt
ε0 − ε∞
0
16
Zunächst Annahme, das φ(t) ∝ e(-t/τ), =) eine Relaxationszeit
ε ′(ν ) − ε ∞
1
=
ε0 − ε∞
1 + ω 2τ 2
ε ′′(ν )
ωτ
=
ε 0 − ε ∞ 1 + ω 2τ 2
(Lorentzkurve)
Exponentielle Relaxation in der Zeit entspricht Lorentzkurve im Energieraum
Halbwertsbreite der Verlustkurve bei
einer Anregung = 1.14 (log ωτ) und
sym. Form um log ωτ = 0
Real: Polymeren zeigen breitere Verlustkurve
meistens asymmetrisch mit längeren Schwanz zu ωτ > 0
⇒ empirische Erweiterung im Frequenzraum
ε (ν ) − ε ∞
1
=
a
ε0 − ε∞
1 + (iωτ )
[
]
b
a=b=1
wie gehabt, eine einzige Anregung
0 < a ≤ 1, b = 1
Cole-Cole Funktion
a = 1, 0 < b ≤ 1
Cole-Davidson Funktion
0 < a ≤ 1, 0 < b ≤ 1 Havriliak-Negami Funktion
⇒ alternativ Einführung einer gestreckten Exponentialfunktion für Relaxation
φ(t) im Zeitraum
φ (t ) ∝ e (− t / τ )
β
mit 0 < β ≤ 1
Kohlrausch-Williams-Watt Funktion
Diese verschiedenen nicht exponentiellen Relaxationsfunktionen haben
allgemeine Anwendungen !!!
17
Beispiel: amorphes Polymer
Polyethylmethacrylate bei 272 K für Drücke von 1(1), 340(2), 690(3),und
1020(4) bar zeigt starke Druckabhängigkeit.
Sehr gute Beschreibung durch KWW Funktion ⇒ Hier wird α-Prozeß, d.h.
langreichweitige strukturelle Relaxation beobachtet.
Alle amorphen Polymere zeigen zwei Relaxationsprozesse,
α-Prozeß für Bewegungen auf großer Skala
β-Prozeß für lokalisierte Bewegung (höhere Frequenzen als α-Prozeß)
18
a) α-Prozeß
⎛
B
⎝ T − T0
τα folgt Vogel-Fulcher-Tamman (VFT)-Gesetz τα = A exp ⎜⎜
⎞
⎟⎟
⎠
α-Prozeß folgt Temperatur-Zeit-Superpositionsprinzip: Normierungsgröße folgt
Williams-Landel-Ferry (WLF)-Gleichung
lnτ 2
C1 (T1 − T2 )
=
lnτ 1 C 2 + (T2 − T1 )
C1 = B / (T1 − T0 );C 2 = T1 − T0
b) β-Prozeß
τβ ist einfach aktiviert (Arrhenius Gerade) mit schwacher T-Abhängigkeit
mündet bei hohen Temperaturen in den α-Prozeß
normalerweise ist Relaxationsstärke Δεα > Δεβ (Ausnahmen möglich)
Was ist die Natur des β-Prozesses?
• Mikroskopisch nicht eindeutig identifiziert
• In Polymeren teilweise Seitenarmbewegungen, lokale Bewegungen der
Hauptkette, partielle Reorientierung der Hauptkette …
Anregungsmaxima zu höheren Frequenzen hin werden als γ−, δ−Relaxationen
bezeichnet:
Beispiel für eine molekulare Zuordnung:
α und β Relaxation sehr verschieden für verschiedene Polymere
19
Superpositionsprinzipien:
Temperatur
Druck
-
Zeit
Superpositionsprinzip ⎫
⎪
⎬beide beobachtet
⎪
Superpositionsprinzip
⎭
Zeit
-
-
Normalisierte Meisterkurve für ε' und ε" für Polyethylacrylate •, †, „
entspricht Daten gemessen mit 1, 340 und 690 bar
α-Prozeß am häufigsten mit Kohlrauschgesetz (KWW) angepaßt: β ~ 0.3 - 0.7
Wo kommt Kohlrausch Relaxationsgesetz her?
• Superposition von vielen Relaxationszeiten, inhomogenes Modell
• Modenkopplung bietet Potenzgesetze, die im α-Bereich gut mit Kohlrausch
übereinstimmen
• Kopplungsmodell von Ngai
Relaxationsrate
dh
= W (t ) ⋅ h
dt
für W(t) = konst. folgt exponentielle Relaxation
für W(t) = W0(ωct)-n, d.h. zeitabhängige Relaxationsrate
folgt
h(t) = exp [– (t/τ)1-n]
und
τ = [ (1-n) ωnc τo ] (1-n)-1
20