Peltier-Wärmepumpe - Universität Hamburg

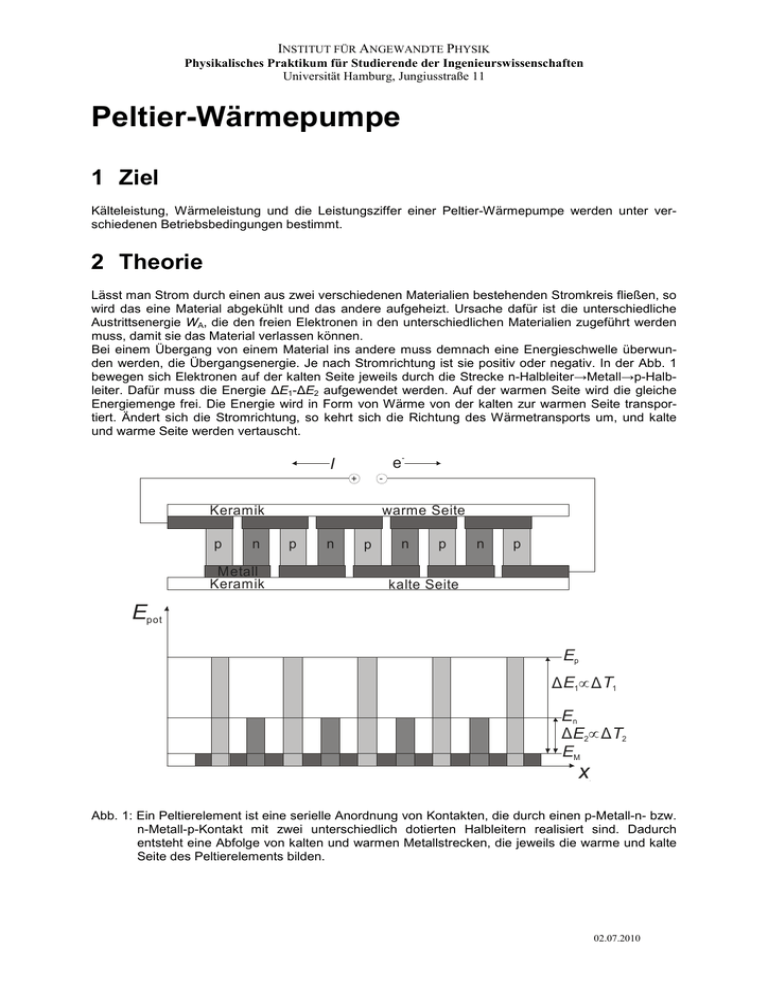
INSTITUT FÜR ANGEWANDTE PHYSIK
Physikalisches Praktikum für Studierende der Ingenieurswissenschaften
Universität Hamburg, Jungiusstraße 11
Peltier-Wärmepumpe
1 Ziel
Kälteleistung, Wärmeleistung und die Leistungsziffer einer Peltier-Wärmepumpe werden unter verschiedenen Betriebsbedingungen bestimmt.
2 Theorie
Lässt man Strom durch einen aus zwei verschiedenen Materialien bestehenden Stromkreis fließen, so
wird das eine Material abgekühlt und das andere aufgeheizt. Ursache dafür ist die unterschiedliche
Austrittsenergie WA, die den freien Elektronen in den unterschiedlichen Materialien zugeführt werden
muss, damit sie das Material verlassen können.
Bei einem Übergang von einem Material ins andere muss demnach eine Energieschwelle überwunden werden, die Übergangsenergie. Je nach Stromrichtung ist sie positiv oder negativ. In der Abb. 1
bewegen sich Elektronen auf der kalten Seite jeweils durch die Strecke n-Halbleiter→Metall→p-Halbleiter. Dafür muss die Energie ∆E1-∆E2 aufgewendet werden. Auf der warmen Seite wird die gleiche
Energiemenge frei. Die Energie wird in Form von Wärme von der kalten zur warmen Seite transportiert. Ändert sich die Stromrichtung, so kehrt sich die Richtung des Wärmetransports um, und kalte
und warme Seite werden vertauscht.
e-
I
-
+
Keramik
p
n
Metall
Keramik
warme Seite
p
n
p
n
p
n
p
kalte Seite
Epot
Ep
∆ E1∝ ∆ T1
En
∆ E2∝ ∆ T2
EM
x, I
Abb. 1: Ein Peltierelement ist eine serielle Anordnung von Kontakten, die durch einen p-Metall-n- bzw.
n-Metall-p-Kontakt mit zwei unterschiedlich dotierten Halbleitern realisiert sind. Dadurch
entsteht eine Abfolge von kalten und warmen Metallstrecken, die jeweils die warme und kalte
Seite des Peltierelements bilden.
02.07.2010
PELTIER -WÄRMEPUMPE
Dieser Effekt ist 1834 von dem Uhrmacher Peltier entdeckt und nach ihm benannt worden. Hierbei ist
die Pumpleistung PP der pro Zeiteinheit t transportierte Wärmemenge Q. Sie ist der Stromstärke I proportional.
T
Q
= PP = π ⋅ I = α ⋅ T ⋅ I
t
(1)
TW
π: Peltierkoeffizient,
α: Seebeck-Koeffizient
TK
T: Absoluttemperatur
Beim reinen Peltiereffekt steigt daher die Temperaturdifferenz zwischen kalter und warmer Seite bei konstantem Strom linear an. Zu beachten ist allerdings, dass
der Peltiereffekt immer in Begleitung anderer Prozesse
auftritt. Diese werden im Folgenden erläutert.
2.1 Joulesche Wärme
t
Abb. 2: Temperaturverlauf der
kalten und warmen Seite
eines Peltierelements
beim reinen Peltiereffekt.
Strom ist die Bewegung von Ladungsträgern. Dabei wird Wärme erzeugt, deren Leistung PJ mit der
Stromstärke I steigt. Von dieser Wärmezufuhr ist die kalte und warme Seite gleichermaßen betroffen.
PJ = U ⋅ I = R ⋅ I 2
(2)
U: Spannung
R: Widerstand des Peltierelementes
2.2 Wärmeleitung
T
Da die warme und kalte Seite in Kontakt zueinander
stehen, wird die wachsende Temperaturdifferenz kompensiert. Die Leistung der Wärmeleitung PL ist proportional zur Temperaturdifferenz TW - TK und führt dazu,
dass sich die Temperaturdifferenz einem konstanten
Wert ∆T annähert.
TW
∆T
TK
A
PL = λ (TW − TK )
d
t
(3)
λ: Wärmeleitfähigkeit des Materials
A,d: Fläche und Dicke des Peltierelements
Abb. 3: Temperaturverlauf der Peltierelement-Seiten, wenn
die Wärmeleitung berücksichtigt wird.
2.3 Thomsoneffekt
Fließt ein Strom in einem Leiter mit einem Temperaturgefälle so kann er je nach Material Wärme aufnehmen oder abgeben. Die Richtung des Wärmeflusses hängt von der Stromrichtung, von dem Vorzeichen des Thomsonkoeffizienten τ und von der Richtung des Temperaturgradienten dT/dx ab. Er
wird beschrieben durch
PT = τ ⋅ I ⋅
PT:
I:
∆T:
dT
∆T
≈τ ⋅I ⋅
dx
d
Leistung des Thomsoneffekts
Stromstärke
Temperaturdifferenz
Die Temperaturdifferenz bleibt konstant.
2
(4)
PELTIER -WÄRMEPUMPE
T
∆T/∆t
Abb. 4: Temperaturverlauf der Seiten eines
Peltierelements bei Berücksichtigung
von Joulescher Wärme, Wärmeleitung
und Thomsoneffekt.
∆T
t
3 Aufgaben
•
Aus der Temperatur- Zeit- Funktion auf der Warmseite und der Kaltseite werden Pumpleistung
in Warm- und Kaltbetrieb, PW , PK und Leistungsziffer in Warm- und Kaltbetrieb ηW , ηK bestimmt.
•
Die Pumpleistung im Wärmebetrieb Pw und die Leistungsziffer ηW werden bei konstanter
Stromstärke und konstanter Temperatur der Kaltseite bestimmt.
•
Bei Luftkühlung der Warmseite werden PK und ηK der Kaltseite bestimmt.
3.1 Durchführung
•
Auf beiden Seiten der Wärmepumpe werden Wasserbehälter befestigt und mit Wasser gleicher Temperatur gefüllt. Bei konstantem Strom IP und konstanter Spannung UP wird die Temperaturänderungen in beiden Wasserbehältern als Funktionen der Zeit TW (t), TK(t) gemessen.
Die Messung erstreckt sich über 20 Minuten.
Zur Auswertung werden die Temperaturen TW und TK gegen die Zeit t aufgetragen. Die Steigung ∆Ti/∆t dieses Verlaufes ist ein Maß für die Wärmepumpleistung Pi, i=W;K.
Aus dem linearen Bereich der Kurve lassen sich
Pi = Cges ⋅
∆Ti
TW =?
∆t
W
K
TK=?
,
sowie die Leistungskennziffern
ηi = Pi Pel mit Pel = I P ⋅ U P
berechnen. Dabei ist
Cges:
Spezifische Wärmekapazität des Gesamtsystems, bestehend aus Wasser,
Messingbehälter und Kupferblock (Cges = 1121 J/K)
∆Ti, ∆t: Temperatur- und Zeitabschnitt des Steigungsdreiecks im linearen Bereich
Pel:
Elektrische Leistung
IP, UP: Strom und Spannung am Peltierelement
3
PELTIER -WÄRMEPUMPE
•
Auf der Warmseite des Peltierelements wird ein Wasserbehälter, auf der Kaltseite ein Durchflusswärmetauscher befestigt, durch welchen Leitungswasser strömt. Der Betriebsstrom wird
so gepolt, dass das Wasser im Wasserbehälter erwärmt wird.
Analog zum Teil 1 werden PW und PK sowie ηW und ηK aus der Steigung der Kurven TW (t) und
TK(t) im linearen Bereich berechnet. Die Ergebnisse sind zu diskutieren.
A
Leitungswasser
IP
0 -18 V
+
TW = ?
V
W
W
K
TK = konst.
UP
•
Auf der Kaltseite des Peltierelements befindet sich ein
Wasserbehälter, auf der Warmseite ein Kühlkörper. Die
Temperatur der Kaltseite wird als Funktion der Zeit gemessen, wobei der Kühlkörper sich in ruhender Umgebungsluft befindet. Dieser Versuchsteil wird, wie die vorhergehenden, für 20 Minuten durchgeführt.
Man trage TK(t) gegen die Zeit auf und diskutiere die Kurven.
4
TK=?
K
W
PELTIER -WÄRMEPUMPE
Anhang
Leistungsbilanz
Im folgenden werden die unterschiedlichen Einflüsse auf das Temperaturverhalten betrachtet. So erhält man für die Wärmepumpleistung auf der Kaltseite mit ∆T = TW - TK:
− PK = PP ,K m
PT PJ
τI∆T I 2 R λA∆T
− − PL = αTK I m
−
−
2
2
2d
2
d
bzw. für die Warmseite:
+ PW = PP ,W ±
PT PJ
τI∆T I 2 R λA∆T
+ − PL = αTW I ±
+
−
2
2
2d
2
d
Die zugeführte elektrische Leistung ist
+ Pel = PP + PJ + PT = U P ⋅ I P
Die Leistungsbilanz ist also graphisch dargestellt:
B
PK
C
A
TK
PP,K
PJ/2
PT/2
Pel
PL
PP
PJ/2
d
PT/2
PP,K
PW
5
TW